| 2\(\dfrac{1}{5}\) - x | + | x - \(\dfrac{1}{5}\) | + 8\(\dfrac{1}{5}\) = 1,2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}2x+3y=-xy\\\dfrac{8}{x}-\dfrac{6}{y}=5\end{matrix}\right.\left(x;y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\8y-6x=5xy\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\6x-8y=-5xy\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\6x-8y=5\left(2x+3y\right)\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\6x-8y=10x+15y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=-xy\\-4x=23y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{-23}{4}y+3y=\dfrac{-23}{4}y\cdot y\\x=\dfrac{-23}{4}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}23y^2-43y=0\\x=\dfrac{-23}{4}y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y\left(23y-43\right)=0\\x=\dfrac{-23}{4}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=0\left(ktm\right)\\y=\dfrac{43}{23}\left(tm\right)\end{matrix}\right.\\x=\dfrac{-23}{4}\cdot\dfrac{43}{23}=\dfrac{-43}{4}\end{matrix}\right.\)

bài giải
số lớn chia số bé được 3 dư 3, số bé bằng 1/3 số lớn
số lớn là:
33 : ( 3 -1 ) x 3 + 3 = 53,5
số bé là:
33: ( 3 - 1 ) = 16,5
đ/s

Gọi chiều dài là a => chiều rộng = a-4
Theo bài ra: a+(a-4)=80
<=> 2a = 84
=> a = 42
=> chiều rộng = a-4 = 42-4 = 38
Diện tích tấm màn là: 38x42= 1596 m2

\(\left\{{}\begin{matrix}\dfrac{8}{\sqrt{x^2+1}}+\dfrac{4}{\sqrt{y^2+1}}=9\\\dfrac{1}{\sqrt{x^2+1}}-\dfrac{1}{\sqrt{y^2+1}}=\dfrac{3}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{\sqrt{x^2+1}}+\dfrac{4}{\sqrt{y^2+1}}=9\\\dfrac{4}{\sqrt{x^2+1}}-\dfrac{4}{\sqrt{y^2+1}}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8}{\sqrt{x^2+1}}+\dfrac{4}{\sqrt{y^2+1}}+\dfrac{4}{\sqrt{x^2+1}}-\dfrac{4}{\sqrt{y^2+1}}=9+3\\\dfrac{1}{\sqrt{x^2+1}}-\dfrac{1}{\sqrt{y^2+1}}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{12}{\sqrt{x^2+1}}=12\\\dfrac{1}{\sqrt{y^2+1}}=1-\dfrac{3}{4}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+1=1\\y^2+1=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2=0\\y^2=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\pm\sqrt{15}\end{matrix}\right.\)

TH1: x<1
Phương trình sẽ trở thành:
\(1-x+2-x+3-x=-4x\)
=>-4x=-3x+6
=>-x=6
=>x=-6(nhận)
TH2: 1<=x<2
Phương trình sẽ trở thành:
\(x-1+2-x+3-x=-4x\)
=>-4x=-x+4
=>-3x=4
=>\(x=-\dfrac{4}{3}\left(loại\right)\)
TH3: 2<=x<3
Phương trình sẽ trở thành:
\(x-1+x-2+3-x=-4x\)
=>x=-4x
=>x=0(loại)
TH4: x>=3
Phương trình sẽ trở thành:
x-1+x-2+x-3=-4x
=>-4x=3x-6
=>-7x=-6
=>\(x=\dfrac{6}{7}\left(loại\right)\)

\(170=17\cdot2\cdot5;290=29\cdot2\cdot5\)
=>\(BCNN\left(170;290\right)=17\cdot29\cdot2\cdot5=4930\)
\(a⋮170;a⋮290\)
=>\(a\in BC\left(170;290\right)\)
mà a nhỏ nhất
nên a=BCNN(170;290)
=>a=4930

a: Oy nằm giữa Ox và Ot
=>\(\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
=>\(\widehat{yOt}+30^0=50^0\)
=>\(\widehat{yOt}=20^0\)
b: Vì Ox là tia đối của tia Oz nên \(\widehat{xOz}=180^0\)
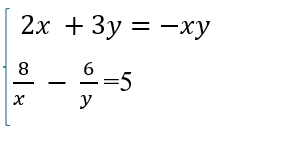

\(\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}=1,2\\\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=1,2-8\dfrac{1}{5}\\ \Rightarrow \left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=-7\)
Nhận xét:
\(\left\{{}\begin{matrix}\left|2\dfrac{1}{5}-x\right|\ge0,\forall x\\\left|x-\dfrac{1}{5}\right|\ge0,\forall x\end{matrix}\right.\\ \Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|\ge0,\forall x\)
Mà \(-7< 0\) nên:
Không tìm được giá trị \(x\) thỏa mãn đề bài
Vậy...