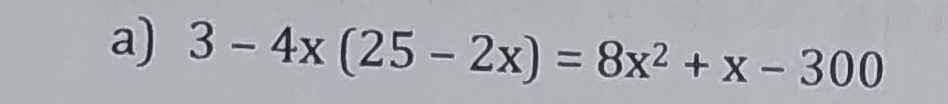 giải pt
giải pt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\notin\left\{0;3;-3;-\dfrac{3}{2}\right\}\)
\(\dfrac{x^2-6}{x-3}+\dfrac{x^2+3x}{2x+3}\left(\dfrac{x}{x^2-9}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\left(\dfrac{x}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\dfrac{x^2-\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x^2-x^2-6x-9}{\left(2x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-6}{x-3}-\dfrac{3}{x-3}=\dfrac{x^2-9}{x-3}=x+3\)

a: Xét ΔCED vuông tại E và ΔCFD vuông tại F có
CD chung
\(\widehat{ECD}=\widehat{FCD}\)
Do đó: ΔCED=ΔCFD
=>CE=CF: DE=DF
Xét ΔCEK vuông tại E và ΔCFH vuông tại F có
CE=CF
\(\widehat{ECK}\) chung
Do đó: ΔCEK=ΔCFH
b: Xét ΔDEH vuông tại E và ΔDFK vuông tại F có
DE=DF
\(\widehat{EDH}=\widehat{FDK}\)
Do đó: ΔDEH=ΔDFK
=>DH=DK
=>D nằm trên đường trung trực của HK(1)
Ta có: CH=CK
=>C nằm trên đường trung trực của HK(2)
Ta có: MH=MK
=>M nằm trên đường trung trực của HK(3)
Từ (1),(2),(3) suy ra C,D,M thẳng hàng

a: \(\text{Δ}=\left(2m+1\right)^2-4\cdot\left(m^2+\dfrac{1}{2}\right)\)
\(=4m^2+4m+1-4m^2-2=4m-1\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-1>0
=>m>1/4
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+\dfrac{1}{2}\end{matrix}\right.\)
\(M=\left(x_1-1\right)\left(x_2-1\right)\)
\(=x_1x_2-\left(x_1+x_2\right)+1\)
\(=m^2+\dfrac{1}{2}-2m-1+1\)
\(=m^2-2m+\dfrac{1}{2}\)
\(=m^2-2m+1-\dfrac{1}{2}=\left(m-1\right)^2-\dfrac{1}{2}>=-\dfrac{1}{2}\forall m\)
Dấu '=' xảy ra khi m-1=0
=>m=1(nhận

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
b: Ta có: MH=MK
mà MK<MC(ΔMKC vuông tại K)
nên MH<MC
c: ΔKAM vuông tại K
=>AM là cạnh lớn nhất trong ΔKAM
=>MK<AM



Tỉ số giữa số sách ở ngăn trên lúc đầu so với tổng số sách là \(\dfrac{1}{4+1}=\dfrac{1}{5}\)
Tỉ số giữa số sách ở ngăn trên lúc sau so với tổng số sách là \(\dfrac{1}{5+1}=\dfrac{1}{6}\)
Tổng số sách là \(4:\left(\dfrac{1}{5}-\dfrac{1}{6}\right)=4:\dfrac{1}{30}=120\left(quyển\right)\)

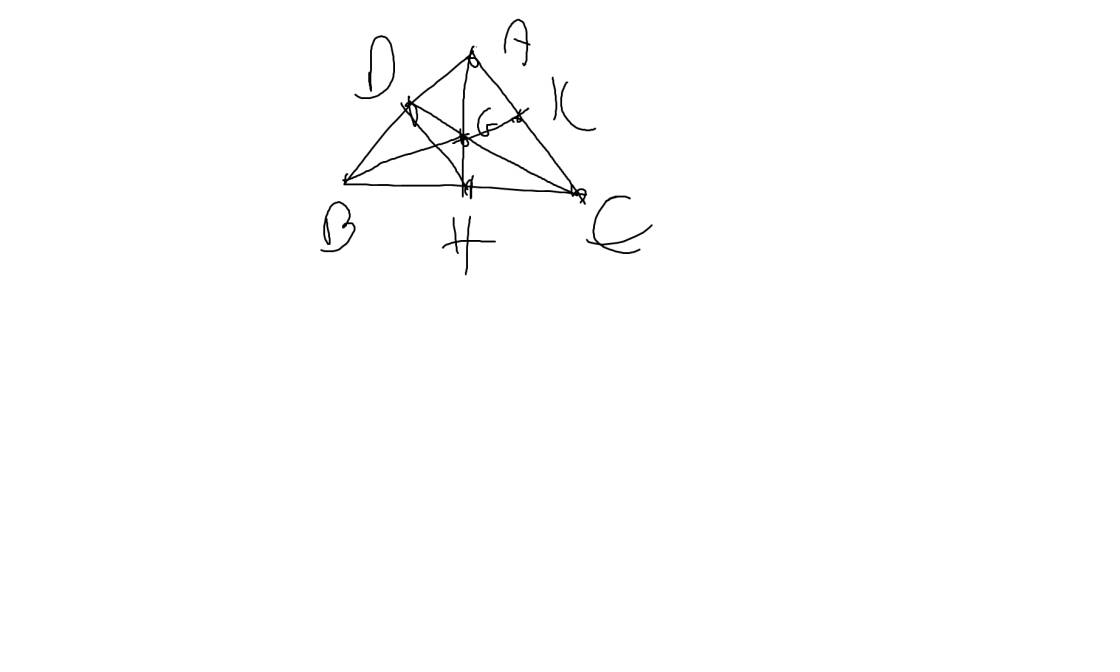
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)
nên \(\widehat{DHA}=\widehat{DAH}\)
=>ΔDAH cân tại D
b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)
\(\widehat{DAH}+\widehat{DBH}=90^0\)
mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DH=DB
=>DA=DB
=>D là trung điểm của AB
Xét ΔABC có
AH,CD là các đường trung tuyến
AH cắt CD tại G
Do đó: G là trọng tâm của ΔABC
c: Xét ΔABC có
G là trọng tâm
Do đó: BG cắt AC tại trung điểm K của AC
TA có:
mà AB=AC
nên AD=DB=AK=KC
Xét ΔDBC và ΔKCB có
DB=KC
BC chung
Do đó: ΔDBC=ΔKCB
=>DC=BK
Xét ΔBAC có
G là trọng tâm
BK là đường trung tuyến
Do đó:
=>2BK=3BG
Trên tia đối của tia KB, lấy E sao cho KB=KE
Xét ΔKAE và ΔKCB có
KA=KC
(hai góc đối đỉnh)
KE=KB
Do đó: ΔKAE=ΔKCB
=>AE=CB
AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

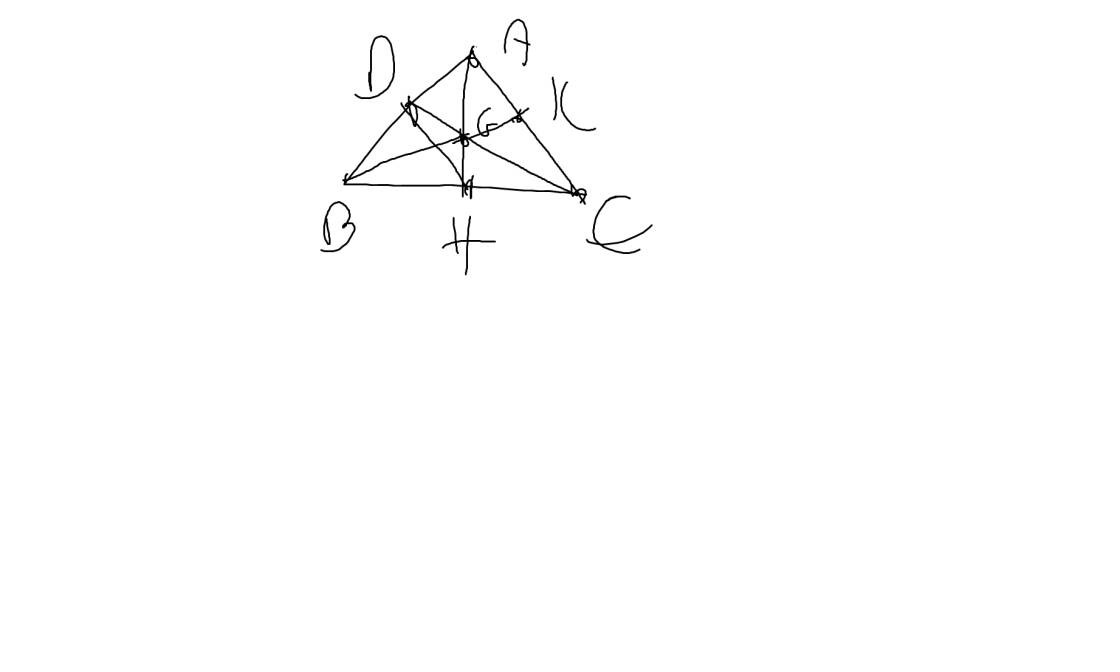
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)
nên \(\widehat{DHA}=\widehat{DAH}\)
=>ΔDAH cân tại D
b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)
\(\widehat{DAH}+\widehat{DBH}=90^0\)
mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DH=DB
=>DA=DB
=>D là trung điểm của AB
Xét ΔABC có
AH,CD là các đường trung tuyến
AH cắt CD tại G
Do đó: G là trọng tâm của ΔABC
c: Xét ΔABC có
G là trọng tâm
Do đó: BG cắt AC tại trung điểm K của AC
TA có: \(AD=DB=\dfrac{AB}{2}\)
\(AK=KC=\dfrac{AC}{2}\)
mà AB=AC
nên AD=DB=AK=KC
Xét ΔDBC và ΔKCB có
DB=KC
\(\widehat{DBC}=\widehat{KCB}\)
BC chung
Do đó: ΔDBC=ΔKCB
=>DC=BK
Xét ΔBAC có
G là trọng tâm
BK là đường trung tuyến
Do đó: \(\dfrac{BG}{BK}=\dfrac{2}{3}\)
=>2BK=3BG
Trên tia đối của tia KB, lấy E sao cho KB=KE
Xét ΔKAE và ΔKCB có
KA=KC
\(\widehat{AKE}=\widehat{CKB}\)(hai góc đối đỉnh)
KE=KB
Do đó: ΔKAE=ΔKCB
=>AE=CB
AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC
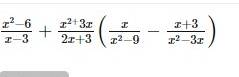 giúp tui zới mn oi bí quá
giúp tui zới mn oi bí quá
3 - 4x(25 - 2x) = 8x² + x - 300
3 - 100x + 8x² = 8x² + x - 300
-100x + 8x² - 8x² - x = -300 - 3
-101x = -303
x = -303 : (-101)
x = 3
Vậy S = {3}