??? bản thân tự giải đi đừng dùng trí tuệ nhân tạo giả nữa. Xin bạn hãy giả tử tế cho mình

x^2 - 5xy - 24y^2 = (ax + by)(cx + dy)

Để tìm a và b, ta có thể sử dụng phương pháp phân tích nhân tử hoặc giải hệ phương trình. Trong trường hợp này, ta sẽ sử dụng phương pháp phân tích nhân tử.

Đầu tiên, ta xem x^2 - 5xy - 24y^2 có thể phân tích thành nhân tử như sau:

x^2 - 5xy - 24y^2 = (px + qy)(rx + sy)

Trong đó, p, q, r, s là các số cần tìm.

Tiếp theo, ta nhân hai ngoặc vuông:

(px + qy)(rx + sy) = p(rx + sy)x + q(rx + sy)y
= prx^2 + psxy + qrxy + qsy^2

So sánh với biểu thức ban đầu, ta có hệ phương trình sau:

pr = 1
ps + qr = -5
qs = -24

Từ hệ phương trình trên, ta có thể tìm các giá trị của p, q, r, s. Sau khi tìm được các giá trị này, ta có thể viết lại biểu thức ban đầu dưới dạng nhân tử.

Gọi 3 số lần lượt là n; n+1; n+2

3 tích lần lượt là: 

\(n\left(n+1\right)=n^2+n\\ n\left(n+2\right)=n^2+2n\\ \left(n+1\right)\left(n+2\right)=n^2+3n+2\)

Theo đề bài, ta có:

\(n^2+n+n^2+2n+n^2+3n+2=242\\ \Leftrightarrow3n^2+6n-240=0\\ \Leftrightarrow3\left(n-8\right)\left(n+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}n=8\\n=-10\end{matrix}\right.\)

Vậy bộ 3 số đó là \(\left\{8;9;10\right\},\left\{-10;-9;-8\right\}\)

a, đều cùng có giá trị dương:
- Để các đơn thức có giá trị dương, ta cần xác định dấu của các biến x, y, z, t.
- Trong các đơn thức đã cho, chỉ có đơn thức thứ nhất (x^3y^2z) không có dấu trừ.
- Vậy, ta có thể xác định dấu của x, y, z, t là dương.

b, đều có giá trị âm thanh giống nhau:
- Để các đơn thức có giá trị âm thanh giống nhau, ta cần xác định dấu của các biến x, y, z, t.
- Trong các đơn thức đã cho, chỉ có đơn thức thứ ba (-3x^2yzt) có dấu trừ.
- Vậy, ta có thể xác định dấu của x, y, z, t là âm

Ta có: \(10^{n+1}-10^n=10^n\left(10-1\right)=9\cdot10^n\)

Mà UCLN\(\left(9\cdot10^n;17\right)\) = 1 

⇒ \(10^{n+1}-10^n\) không chia hết cho 17 với mọi số nguyên x.

\(\left(x-5\right)^3-2y\left(5-x\right)^2\\ =\left(x-5\right)^2\left(x-5-2y\right)\)

\(\dfrac{x+1}{x+2}:\dfrac{x+2}{x+3}:\dfrac{x+3}{x+1}\)

\(=\dfrac{x+1}{x+2}\dfrac{x+3}{x+2}.\dfrac{x+1}{x+3}\)

\(=\dfrac{\left(x+1\right)^2}{\left(x+2\right)^2}\)

\(=\left(\dfrac{x+1}{x+2}\right)^2\)

\(P\left(x\right)=-2x^4-7x+\dfrac{1}{2}-6x^4+2x^2-x\)

\(P\left(x\right)=\left(-2x^4-6x^4\right)-\left(7x+x\right)+2x^2+\dfrac{1}{2}\)

\(P\left(x\right)=-8x^4-8x+2x^2+\dfrac{1}{2}\)

______

\(Q\left(x\right)=3x^3-x^4-5x^2+x^3-6x+\dfrac{3}{4}\)

\(Q\left(x\right)=\left(3x^3+x^3\right)-x^4-5x^2-6x+\dfrac{3}{4}\)

\(Q\left(x\right)=4x^3-x^4-5x^2-6x+\dfrac{3}{4}\)

giúp tuôi nốt phần b với mng ưii

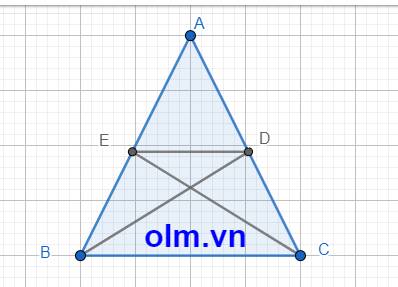
\(\Delta\)ABC cân tại A ⇒ \(\widehat{ABC}\) = \(\widehat{ACB}\)   

\(\widehat{ABD}=\widehat{DBC}\) = \(\dfrac{1}{2}\widehat{ABC}\) (vì BD là phân giác của \(\widehat{ABC}\))

\(\widehat{ACE}\) = \(\widehat{ECB}\) = \(\dfrac{1}{2}\)\(\widehat{ACB}\) (vì CE là phân giác của \(\widehat{ACB}\))

⇒ \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\) (1)

Xét \(\Delta\)BCE và  \(\Delta\)CBD có:

\(\widehat{EBC}\) = \(\widehat{BCD}\) (vì tam giác ABC cân tại A)

\(\widehat{ECB}\) = \(\widehat{DBC}\)  theo (1) 

Và BC chung 

\(\Rightarrow\) \(\Delta\)BCE = \(\Delta\) CBD (g-c-g) ⇒ BE = CD ⁽²⁾

BE + EA = AD + DC (vì \(\Delta\)ABC cân tại A)

⇒ AE = AD \(\Rightarrow\) \(\dfrac{AE}{AB}\) = \(\dfrac{AD}{AC}\) \(\Rightarrow\) ED // BC ⁽³⁾ (định lý talet đảo)

\(\widehat{DBC}\) = \(\widehat{BDE}\) (so le trong)

⇒\(\widehat{EBD}\) = \(\widehat{BDE}\) (vì cùng bằng góc DBC)

⇒ \(\Delta\)BDE cân tại E \(\Rightarrow\) BE = ED ⁽⁴⁾

Kết hợp (2); (3); (4) ta có

Tứ giác BECD là hình thang cân có đáy nhỏ bằng cạnh bên. (đpcm)

a) \(f\left(x\right)+g\left(x\right)+h\left(x\right)\)

\(=6x^7-5x^3+1-3+2x-4x^7-2x^7+2x+7x^2\)

\(=-5x^3+7x^2+4x-2\)

b) \(f\left(x\right)+g\left(x\right)-h\left(x\right)\)

\(=6x^7-5x^3+1-3+2x-4x^7-\left(-2x^7+2x+7x^2\right)\)

\(=2x^7-5x^3+2x-2+2x^7-2x-7x^2\)

\(=4x^7-5x^3-7x^2-2\)

Đề bài sai rồi, xem lại bạn ơi