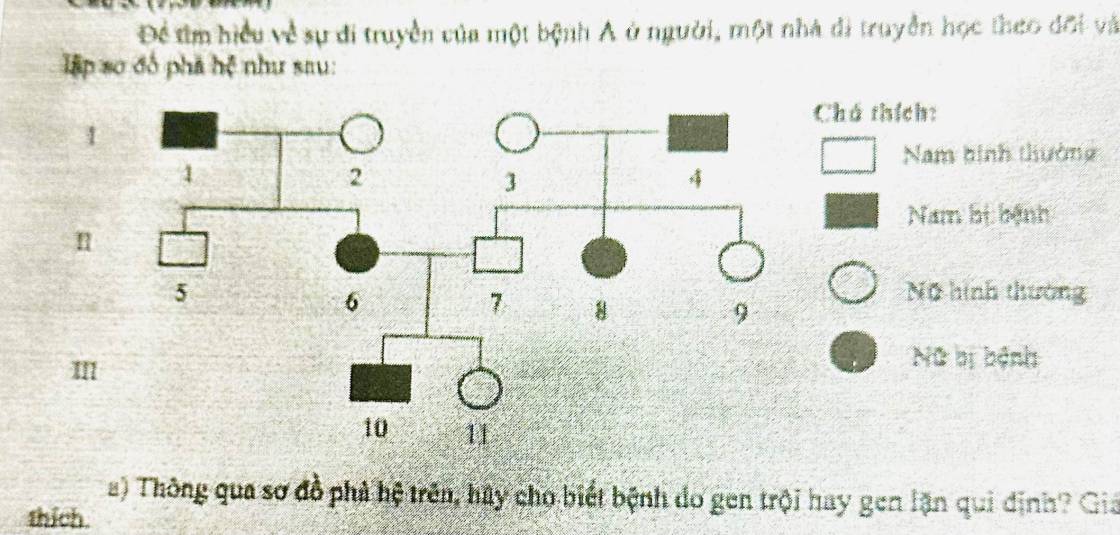
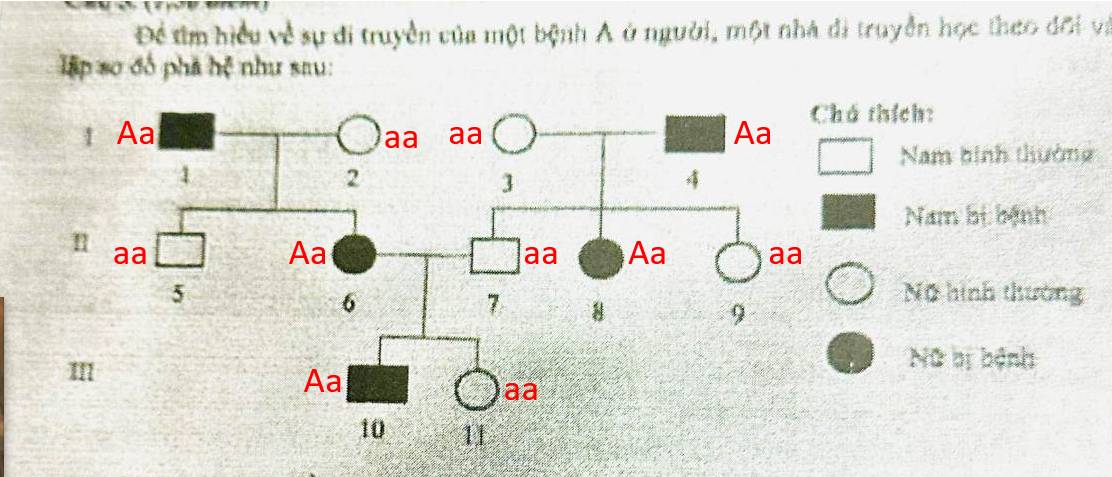
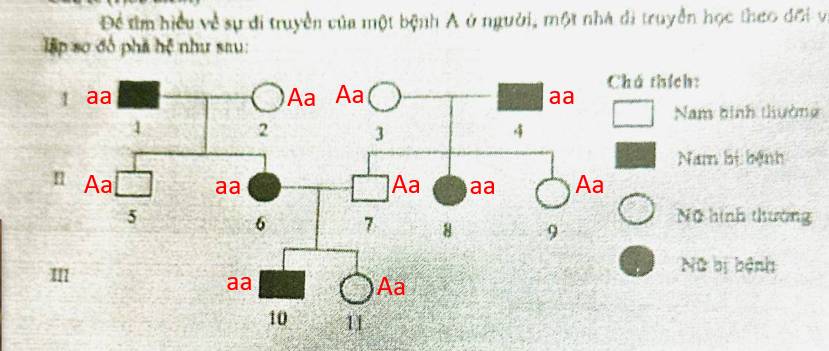
Trong một giải đấu cờ vua có 5 vận động viên thi đấu vòng tròn một lượt; nghĩa là mỗi vận động viên đấu với 4 vận động viên còn lại mỗi người một trận. Với cách tính điểm của mỗi trận đấu là: vận động viên thắng thì được 1 điểm, vận động viên hoà thì được 0,5 điểm, vận động viên thua thì không có điểm. Biết rằng, sau khi kết thúc giải đấu mỗi vận động viên đều nhận được điểm số khác nhau và được xếp hạng từ cao đến thấp là nhất, nhì, đến ba, tư, năm dựa vào số điểm
đạt được (số điểm đạt được càng nhiều thì thứ hạng càng cao). Ngoài ra:
- Vận động viên xếp hạng nhất không hoà trận nào.
- Vận động viên xếp hạng nhì không thua trận nào.
- Vận động viên xếp hạng tư không thắng trận nào.
a) Giải đấu đã tổ chức tất cả bao nhiêu trận đấu? Vận động xếp viên hạng nhất được bao nhiêu điểm?
b) Em hãy xác định điểm số của mỗi vận động viên còn lại (vận động viên xếp hạng nhì, hạng ba, hạng tư, hạng năm) và chi tiết kết quả các trận đấu của từng vận động viên.