\(Q=x^2(x+1)-3xy(x-y+1)-y^2(y-1)+xy\\=x^3+x^2+3xy(y-x)-3xy-y^3+y^2+xy\\=-(y^3-x^3)+3xy(y-x)+x^2-2xy+y^2\\=-(y-x)^3-3xy(y-x)+3xy(y-x)+(y-x)^2\\=-11^3+11^2=-1210\)

Chỉ ra thành phần biệt lập: Đấy, mày nghe chưa?.

Phân tích tác dụng: thể hiện chi tiết hơn tâm lý, suy nghĩ của nhân vật người chú từ đó tăng giá trị diễn đạt cảm xúc, câu văn thêm hay hơn, hấp dẫn người đọc hơn.

b. Cần ngữ liệu 

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\)

\(\Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]-105=0\)

\(\Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)-105=0\) (1)

Đặt \(x^2+10x+20=t\), khi đó (1) trở thành:

\(\left(t-4\right)\left(t+4\right)-105=0\)

\(\Leftrightarrow t^2-16-105=0\)

\(\Leftrightarrow t^2-11^2=0\)

\(\Leftrightarrow\left(t-11\right)\left(t+11\right)=0\)

\(\Rightarrow\left(x^2+10x+20-11\right)\left(x^2+10x+20+11\right)=0\)

\(\Leftrightarrow\left(x^2+10x+9\right)\left(x^2+10x+31\right)=0\)

\(\Leftrightarrow\left(x^2+9x+x+9\right)\left[\left(x+5\right)^2+6\right]=0\)

\(\Leftrightarrow x\left(x+9\right)+\left(x+9\right)=0\) (vì \(\left(x+5\right)^2+6>0;\forall x\))

\(\Leftrightarrow\left(x+9\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+9=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=-1\end{matrix}\right.\)

Vậy phương trình đã cho có tập nghiệm là $S=\{-9;-1\}$.

$Toru$

\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)-105=0\\ \Leftrightarrow\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]=105\\ \Leftrightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)=105\\ \Leftrightarrow\left(x^2+10x+20-4\right)\left(x^2+10x+20+4\right)=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2-4^2=105\\ \Leftrightarrow\left(x^2+10x+20\right)^2=121\\ \)

\(\Rightarrow\left[{}\begin{matrix}x^2+10x+20=11\left(1\right)\\x^2+10x+20=-11\left(2\right)\end{matrix}\right.\)

Giải (1):

\(x^2+10x+9=0\\ \Leftrightarrow\left(x^2+x\right)+\left(9x+9\right)=0\\ \Leftrightarrow x\left(x+1\right)+9\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+9\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-9\end{matrix}\right.\)

Giải (2):

Nhận thấy: \(x^2+10x+20=\left(x+5\right)^2-5\ge-5\forall x\inℝ\)

Vậy pt (2) vô nghiệm

Vậy tập nghiệm pt là: \(S=\left\{-1;-9\right\}\)

Mình nghĩ là bằng nhau.

`060° = 60°`nhé

-> You are not allowed to smoke in this restaurant.

-> You should not have entered my room without asking me first.

-> Will you be able to participate in the race next Thursday?

=> You are not allowed to smoke in this restaurant.

=> You should have asked me first before coming into my room.

=> Will you be able to take part in the race next Thursday?

1: BC=BH+CH=4+9=13(cm)

Xét ΔHAB vuông tại H và ΔACB vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHAB~ΔACB

=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC=4\cdot13=52\)

=>\(BA=\sqrt{52}=2\sqrt{13}\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)

=>\(AC=\sqrt{117}=3\sqrt{13}\left(cm\right)\)

2: ΔHAB~ΔACB

=>\(\dfrac{HA}{AC}=\dfrac{AB}{CB}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{13}\cdot3\sqrt{13}}{13}=6\left(cm\right)\)

Xét tứ giác AKHE có \(\widehat{AKH}=\widehat{AEH}=\widehat{KAE}=90^0\)

nên AKHE là hình chữ nhật

=>AH=KE

=>KE=6(cm)

3: Xét ΔAKH vuông tại K và ΔAHB vuông tại H có

\(\widehat{HAB}\) chung

Do đó: ΔAKH~ΔAHB

=>\(\dfrac{AK}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AK\cdot AB\left(1\right)\)

Xét ΔAEH vuông tại E và ΔAHC vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHC

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AE\cdot AC\left(2\right)\)

Từ (1),(2) suy ra \(AK\cdot AB=AE\cdot AC\)

=>\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Xét ΔAKE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔAKE~ΔACB

4: ta có: ΔABC vuông tại A

mà AI là đường trung tuyến

nên IA=IC

=>ΔIAC cân tại I

=>\(\widehat{IAC}=\widehat{ICA}\)

ΔAKE~ΔACB

=>\(\widehat{AEK}=\widehat{ABC}\)

Ta có: \(\widehat{AEK}+\widehat{IAC}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>EK\(\perp\)AI tại N

1. Tính AB, AC:

• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AB² = AH² + HB²
  • AH² = AB² - HB²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AC² = AH² + HC²
  • AH² = AC² - HC²
• Từ hai phương trình trên, ta có: AB² - HB² = AC² - HC²
• Suy ra: AB² = AC² - HC² + HB²
• Thay số: AB² = AC² - 9² + 4² = AC² - 65
• Áp dụng định lý Pitago trong tam giác vuông ABC:
  • BC² = AB² + AC²
  • BC² = (AC² - 65) + AC² = 2AC² - 65
• Thay BC = HB + HC = 4 + 9 = 13
  • 13² = 2AC² - 65
  • 2AC² = 13² + 65 = 224
  • AC² = 112
  • AC = √112 = 4√7 cm
• Thay AC vào phương trình AB² = AC² - 65:
  • AB² = (4√7)² - 65 = 112 - 65 = 47
  • AB = √47 cm

2. Tính KE:

• Áp dụng định lý Pitago trong tam giác vuông AKE:
  • KE² = AK² + AE²
• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AK² = AH² - HK²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AE² = AH² - HE²
• Thay vào phương trình KE²:
  • KE² = (AH² - HK²) + (AH² - HE²) = 2AH² - (HK² + HE²)
• Ta có: HK + HE = BC = 13 cm
• Áp dụng định lý Pitago trong tam giác vuông HKE:
  • KE² = HK² + HE² = (HK + HE)² - 2HK.HE = 13² - 2HK.HE
• Suy ra: 2AH² - (HK² + HE²) = 13² - 2HK.HE
• 2AH² = 13² + 2HK.HE
• AH² = (13² + 2HK.HE) / 2
• Thay AH² = AB² - HB²:
  • AB² - HB² = (13² + 2HK.HE) / 2
  • 2(AB² - HB²) = 13² + 2HK.HE
  • 2HK.HE = 2(AB² - HB²) - 13²
  • HK.HE = (AB² - HB²) - 13²/2
  • HK.HE = (47 - 4²) - 13²/2 = -65/2
• Vì HK và HE đều dương nên HK.HE = -65/2 là vô lý.
• Vậy, không thể tính KE bằng cách này.

3. Chứng minh AB.AK = AE.AC; AKE ~ ACB:

• Chứng minh AB.AK = AE.AC:
  • Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
    • Góc BAH = Góc CAH (cùng bằng 90 độ)
    • Góc ABH = Góc ACH (cùng phụ với góc BAH)
  • Suy ra tam giác AHB đồng dạng với tam giác AHC (g-g)
  • Do đó: AB/AC = AH/AH = 1
  • Suy ra: AB = AC
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
  • Do đó: AK/AC = AE/AB
  • Suy ra: AB.AK = AE.AC
• Chứng minh AKE ~ ACB:
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)

4. Chứng minh AI vuông góc KE tại N:

• Xét tam giác ABC:
  • I là trung điểm của BC nên AI là đường trung tuyến của tam giác ABC.
• Xét tam giác AKE:
  • N là giao điểm của AI và KE nên N là trọng tâm của tam giác AKE.
• Theo tính chất trọng tâm của tam giác:
  • Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
  • Do đó: AN = 2/3 AI
• Xét tam giác vuông AHI:
  • AI là đường trung tuyến của tam giác vuông AHI nên AI = 1/2 HI.
• Suy ra:
  • AN = 2/3 AI = 2/3 * (1/2 HI) = 1/3 HI
  • Do đó: IN = AI - AN = 1/2 HI - 1/3 HI = 1/6 HI
• Xét tam giác vuông HKE:
  • N là trung điểm của KE nên HN là đường trung tuyến của tam giác vuông HKE.
• Theo tính chất đường trung tuyến của tam giác vuông:
  • Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
  • Do đó: HN = 1/2 KE
• Suy ra:
  • IN = 1/6 HI = 1/2 HN
  • Do đó: HN = 3IN
• Xét tam giác HIN:
  • HN = 3IN nên tam giác HIN vuông tại I (định lý đảo của định lý Pytago).
• Kết luận:
  • AI vuông góc KE tại N.

Lưu ý:

• Trong bài toán này, không thể tính KE bằng cách sử dụng định lý Pitago trong tam giác vuông HKE vì HK.HE là một số âm.
• Việc chứng minh AB.AK = AE.AC và AKE ~ ACB là cần thiết để chứng minh AI vuông góc KE tại N.
• Việc chứng minh AI vuông góc KE tại N là một ứng dụng của tính chất trọng tâm của tam giác và tính chất đường trung tuyến của tam giác vuông.
•  

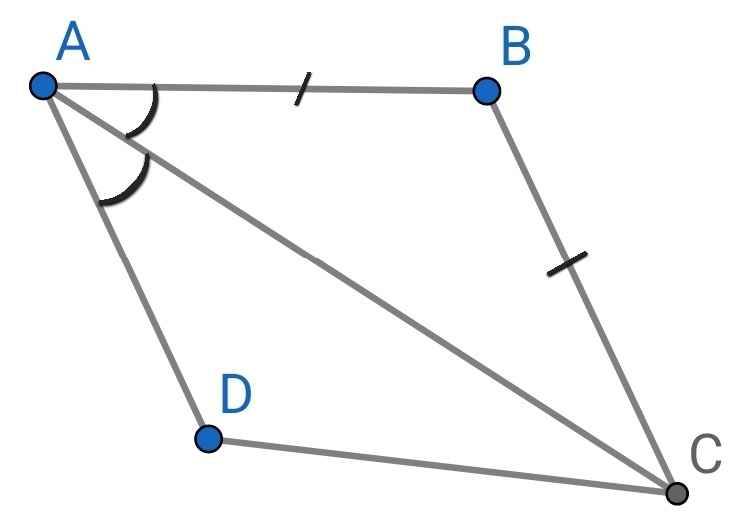
∆ABC có:

AB = BC (gt)

⇒ ∆ABC cân tại B

⇒ ∠BAC = ∠BCA (1)

Do AC là tia phân giác của ∠BAD (gt)

⇒ ∠DAC = ∠BAC (2)

Từ (1) và (2) ⇒ ∠BCA = ∠DAC

Mà ∠BCA và ∠DAC là hai góc so le trong

⇒ BC // AD

⇒ ABCD là hình thang

1. Chứng minh hợp kim tan hết:

• Xét phản ứng của Fe với H2SO4:
  • Fe + H2SO4 → FeSO4 + H2
  • n(Fe) = m(Fe) / M(Fe)
  • n(H2SO4) = C(H2SO4) * V(H2SO4) = 0,2 mol
  • Từ phương trình phản ứng, ta thấy n(Fe) = n(H2SO4) = 0,2 mol
  • m(Fe) = n(Fe) * M(Fe) = 11,2 gam
• Xét phản ứng của Ni với H2SO4:
  • Ni + H2SO4 → NiSO4 + H2
  • n(Ni) = m(Ni) / M(Ni) = (36,2 - 11,2) / 58,7 = 0,42 mol
  • n(H2SO4) = 0,2 mol
  • Từ phương trình phản ứng, ta thấy n(Ni) > n(H2SO4)
• Kết luận:
  • Hợp kim tan hết vì lượng H2SO4 đủ để phản ứng với cả Fe và Ni.

2. Hợp kim gấp đôi có tan hết hay không?

• Lượng Fe và Ni gấp đôi:
  • m(Fe) = 2 * 11,2 = 22,4 gam
  • m(Ni) = 2 * (36,2 - 11,2) = 50 gam
• Lượng H2SO4 không đổi:
  • n(H2SO4) = 0,2 mol
• Xét phản ứng:
  • n(Fe) = m(Fe) / M(Fe) = 0,4 mol
  • n(Ni) = m(Ni) / M(Ni) = 0,86 mol
  • Từ phương trình phản ứng, ta thấy n(Fe) + n(Ni) > n(H2SO4)
• Kết luận:
  • Hợp kim gấp đôi sẽ không tan hết vì lượng H2SO4 không đủ để phản ứng với cả Fe và Ni.

3. Tính khối lượng kim loại trong hợp kim:

• Tính lượng H2 sinh ra:
  • n(H2) = m(CuO) / M(CuO) = 48 / 80 = 0,6 mol
• Tính lượng Fe và Ni:
  • n(Fe) = n(H2) = 0,6 mol
  • n(Ni) = n(H2) - n(Fe) = 0,6 - 0,6 = 0 mol
• Tính khối lượng Fe và Ni:
  • m(Fe) = n(Fe) * M(Fe) = 0,6 * 56 = 33,6 gam
  • m(Ni) = n(Ni) * M(Ni) = 0 * 58,7 = 0 gam
• Kết luận:
  • Khối lượng Fe trong hợp kim là 33,6 gam.
  • Khối lượng Ni trong hợp kim là 0 gam.

Lưu ý:

• Trong bài toán này, ta giả định rằng phản ứng xảy ra hoàn toàn.
• Nồng độ của dung dịch H2SO4 là 0,2M, không phải 0,耀M như trong đề bài.

Hy vọng bài giải này giúp bạn hiểu rõ hơn về bài toán.

a: Xét ΔAEF có

AH là đường cao

AH là đường phân giác

Do đó: ΔAEF cân tại A

Xét ΔAEF có BM//EF

nên \(\dfrac{AB}{AE}=\dfrac{AM}{AF}\)

mà AE=AF

nên AB=AM

=>ΔABM cân tại A

b: Kẻ BK//AC(K\(\in\)EF)

Xét tứ giác BMFK có

BM//FK

BK//MF

DO đó: BMFK là hình bình hành

=>BK=MF

Xét ΔBDK và ΔCDF có

\(\widehat{BDK}=\widehat{CDF}\)(hai góc đối đỉnh)

DB=DC

\(\widehat{DBK}=\widehat{DCF}\)(BK//CF)

Do đó: ΔBDK=ΔCDF

=>BK=CF

Ta có: BK//FC

=>\(\widehat{BKE}=\widehat{AFE}\)

=>\(\widehat{BKE}=\widehat{BEK}\)

=>BE=BK

mà BK=FC và BK=MF

nên MF=BE=CF

\(\left(2x-3\right)^2-\left(x-5\right)\left(4x^2-1\right)=7x+6\)

=>\(4x^2-12x+9-\left(4x^3-x-20x^2+5\right)=7x+6\)

=>\(4x^2-12x+9-4x^3+20x^2+x-5-7x-6=0\)

=>\(-4x^3+24x^2-18x-2=0\)

=>\(-4x^3+4x^2+20x^2-20x+2x-2=0\)

=>\(-4x^2\left(x-1\right)+20x\left(x-1\right)+2\left(x-1\right)=0\)

=>\(\left(x-1\right)\left(-4x^2+20x+2\right)=0\)

=>\(\left[{}\begin{matrix}x-1=0\\-4x^2+20x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5\pm3\sqrt{3}}{2}\end{matrix}\right.\)

mong các bạn giúp đỡ 

ngày 12/6 là mình đi học rồi vào buổi sáng