Cho tam giác abc vuông tại c , cd là phân giác , bc=a, ac =b. Chứng minh cd=a.b/(a+b). sin45
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
ĐKXĐ: $x>1; x\neq 2$
\(B=\frac{\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}}{\sqrt{x^2-4x+4}}.\frac{x-2}{x-1}\)
\(=\frac{\sqrt{(x-1)-2\sqrt{x-1}+1}+\sqrt{(x-1)+2\sqrt{x-1}+1}}{\sqrt{(x-2)^2}}.\frac{x-2}{x-1}\)
\(=\frac{\sqrt{(\sqrt{x-1}-1)^2}+\sqrt{(\sqrt{x-1}+1)^2}}{|x-2|}.\frac{x-2}{x-1}\)
\(=\frac{|\sqrt{x-1}-1|+|\sqrt{x-1}+1|}{|x-2|}.\frac{x-2}{x-1}\)
Nêu $x>2$ thì: \(B=\frac{\sqrt{x-1}-1+\sqrt{x-1}+1}{x-2}.\frac{x-2}{x-1}=\frac{2\sqrt{x-1}}{x-2}.\frac{x-2}{x-1}=\frac{2}{\sqrt{x-1}}\)
Nếu $1< x< 2$ thì:
\(B=\frac{1-\sqrt{x-1}+\sqrt{x-1}+1}{2-x}.\frac{x-2}{x-1}=\frac{2}{1-x}\)
b.
TH $1< x< 2$ thì không có giá trị $x$ nguyên nào thỏa mãn
TH $x>2$ thì để $B$ nguyên thì $\sqrt{x-1}$ là ước của $2$
$\Rightarrow \sqrt{x-1}\in \left\{1;2\right\}$
$\Rightarrow x\in \left\{2; 5\right\}$
Vì $x>2$ nên $x=5$

\(\sqrt{x+1+\sqrt{x+\dfrac{3}{4}}}=x+1\)
\(\Leftrightarrow\sqrt{\left(x+\dfrac{3}{4}\right)+\sqrt{x+\dfrac{3}{4}}+\dfrac{1}{4}}=x+1\)
\(\Leftrightarrow\left|\sqrt{x+\dfrac{3}{4}}+\dfrac{1}{2}\right|=x+1\)
\(\Leftrightarrow\sqrt{x+\dfrac{3}{4}}+\dfrac{1}{2}=x+1\) (do \(\sqrt{x+\dfrac{3}{4}}+\dfrac{1}{2}>0\))
\(\Leftrightarrow\sqrt{x+\dfrac{3}{4}}=x+\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{2}\ge0\\\left(x+\dfrac{1}{2}\right)^2=x+\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x^2+x+\dfrac{1}{4}=x+\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\x^2-\dfrac{1}{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\\left(x-\dfrac{\sqrt{2}}{2}\right)\left(x+\dfrac{\sqrt{2}}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{\sqrt{2}}{2}\left(nhận\right)\\x=\dfrac{-\sqrt{2}}{2}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\sqrt{2}}{2}\)
- Vậy phương trình có nghiệm duy nhất là \(x=\dfrac{\sqrt{2}}{2}\)

\(ĐKXĐ:x>0;x\ne4;x\ne9\)
\(A=\left(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}\right):\left(\dfrac{x-2}{x-\sqrt{x}-2}-1\right)\)
\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}:\dfrac{x-2-\left(x-\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-9-\left(x-4\right)+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}:\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}:\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x-2}}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
b. \(P=2A-\dfrac{1}{x}=\dfrac{2\sqrt{x}+2}{\sqrt{x}}-\dfrac{1}{x}=2+\dfrac{2}{\sqrt{x}}-\dfrac{1}{x}\)
- Đặt \(t=\dfrac{1}{\sqrt{x}}\left(t>0\right)\). Khi đó:
\(P=2+2t-t^2=-\left(t^2-2t+1\right)+3=-\left(t-1\right)^2+3\le3\)
- Dấu "=" xảy ra khi \(\left(t-1\right)^2=0\Leftrightarrow t=1\Leftrightarrow\dfrac{1}{\sqrt{x}}=1\Leftrightarrow x=1\left(tmĐKXĐ\right)\)
- Vậy \(MaxP=3\), đạt tại \(x=1\)

\(\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\\ =\sqrt{25+2.5.\sqrt{2}+2}-\sqrt{16+2.4.\sqrt{2}+2}\\ =\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}\\ =5+\sqrt{2}-4-\sqrt{2}\\ =1\)
Ta có: \(\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=\sqrt{25+2.5\sqrt{2}+2}-\sqrt{16+2.4\sqrt{2}+2}\)
\(=\sqrt{5^2+2.5\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{4^2+2.4\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}\)
\(=\left|5+\sqrt{2}\right|-\left|4+\sqrt{2}\right|=5+\sqrt{2}-4-\sqrt{2}=1\)


Ta có : \(2x^2-9x+2=\left(6x-3\right)\sqrt{x^2+1}\)
\(\Leftrightarrow2\left(x^2+1\right)-9x=6x\sqrt{x^2+1}-3\sqrt{x^2+1}\)
\(\Leftrightarrow\sqrt{x^2+1}\left(2\sqrt{x^2+1}+3\right)-3x\left(2\sqrt{x^2+1}+3\right)=0\)
\(\Leftrightarrow\left(2\sqrt{x^2+1}+3\right)\left(\sqrt{x^2+1}-3x\right)=0\)
\(\Leftrightarrow\sqrt{x^2+1}=3x\left(\text{vì }2\sqrt{x^2+1}+3>0\forall x\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>0\\8x^2=1\end{matrix}\right.\Leftrightarrow x=\dfrac{1}{2\sqrt{2}}\)
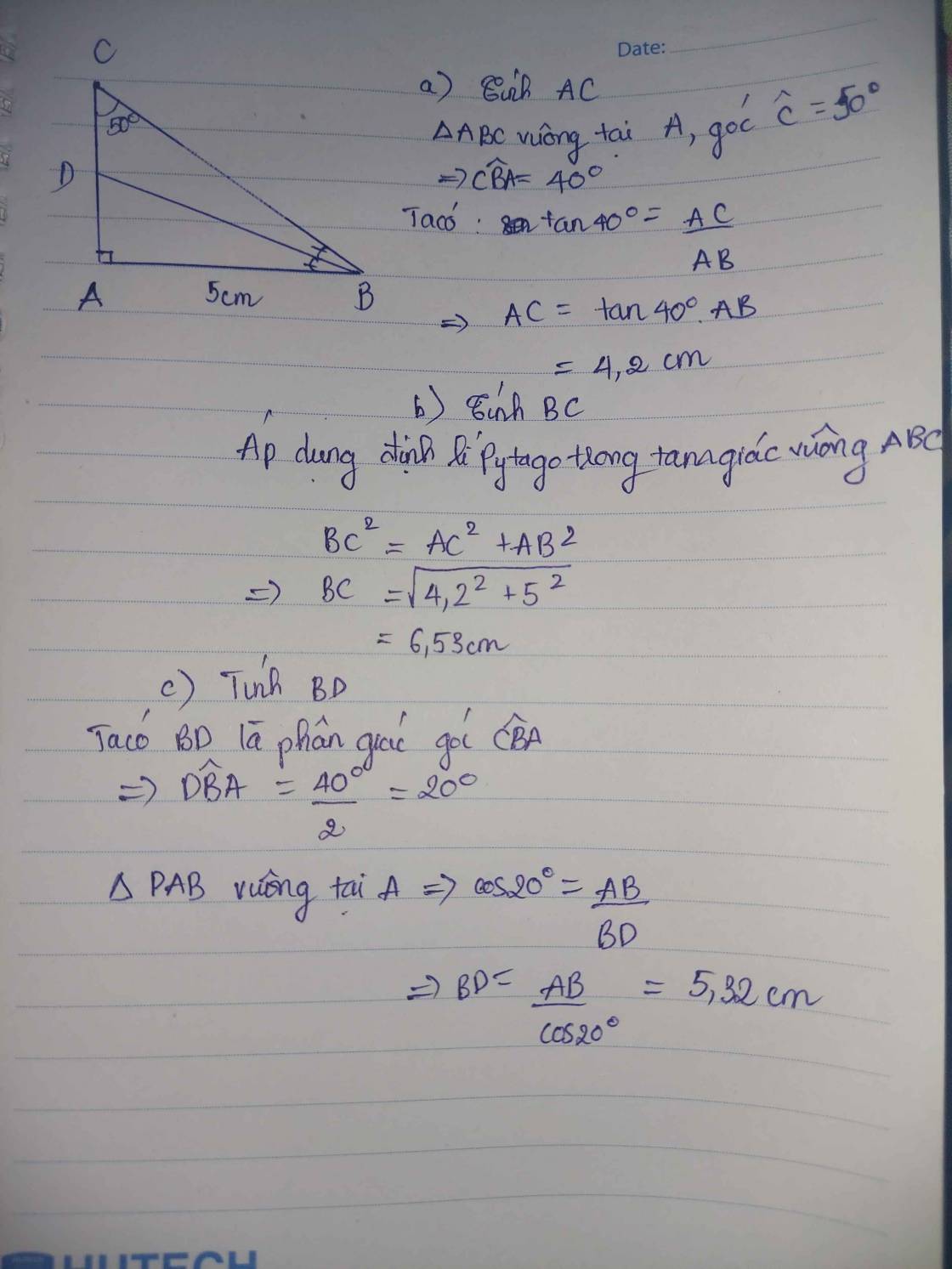
Trên tia đối tia CB lấy điểm P sao cho \(CP=CB=b\). Khi đó dễ thấy \(BP=BC+CP=a+b\) . Để ý rằng \(\Delta ACP\) vuông cân tại C nên \(AP=PC\sqrt{2}=b\sqrt{2}\)
Hơn nữa, do CD là tia phân giác của góc BCA vuông nên \(\widehat{BCD}=45^o\), từ đó suy ra CD//AP do có 2 góc đồng vị là \(\widehat{P}\) và \(\widehat{BCD}\) bằng nhau (vì chúng cùng bằng \(45^o\))
Trong tam giác ABP có CD//AP nên \(\dfrac{CD}{AP}=\dfrac{BC}{BP}\) hay \(CD=\dfrac{AP.BC}{BP}=\dfrac{b\sqrt{2}.a}{a+b}=\dfrac{ab}{\left(a+b\right).\dfrac{1}{\sqrt{2}}}=\dfrac{ab}{\left(a+b\right).sin45^o}\) (đpcm)
gọi E, F lần lượt là chân đường vuông góc hạ từ D xuống AC, CB.
tứ giác DECF có 3 góc vuông và CD là phân giác góc \(\widehat{ECF}\)
=> DECF là hình vuông
gọi x (đvđd) là cạnh hình vuông DECF, CD là đường chéo hình vuông => CD = \(x\sqrt{2}\) (đvđd)
theo Talet: \(\dfrac{BF}{BC}=\dfrac{DF}{AC}\)hay \(\dfrac{a-x}{a}=\dfrac{x}{b}\Rightarrow ba-bx=ax\Rightarrow ab=x\left(a+b\right)\Rightarrow x=\dfrac{ab}{a+b}\)=> \(CD=x\sqrt{2}=\dfrac{ab}{a+b}\sqrt{2}=\dfrac{ab}{\left(a+b\right).\sin45^o}\) (đpcm)