
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: SỐ tiền lãi anh Duy nhận được sau 1 năm là:
\(200\cdot10^6\cdot5,6\%=11200000\left(đồng\right)\)
Số tiền cả gốc lẫn lãi anh Duy nhận được là:
\(200000000+11200000=211200000\left(đồng\right)\)
b: Số tiền lãi năm thứ hai anh Duy nhận được là:
\(211200000\cdot8\%=16896000\left(đồng\right)\)
Tổng số tiền anh Duy nhận được là:
\(211200000+16896000=228096000\left(đồng\right)\)

Ta có:
\(2020+2021+2022< 2021+2022+2023\)
\(\Rightarrow\dfrac{2020+2021+2022}{2021+2022+2023}< 1\)
\(\Rightarrow Q< 1\)
Lại có: \(2020.2>2021.1\Rightarrow\dfrac{2020}{2021}>\dfrac{1}{2}\)
\(2021.2>2022.1\Rightarrow\dfrac{2021}{2022}>\dfrac{1}{2}\)
\(2022.2>2023.1\Rightarrow\dfrac{2022}{2023}>\dfrac{1}{2}\)
\(\Rightarrow\dfrac{2020}{2021}+\dfrac{2021}{2022}+\dfrac{2022}{2023}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=\dfrac{3}{2}\)
\(\Rightarrow P>\dfrac{3}{2}>1\)
\(\Rightarrow P>Q\)
\(\dfrac{2020}{2021}\) > \(\dfrac{2020}{2021+2022+2023}\)
\(\dfrac{2021}{2022}\) > \(\dfrac{2021}{2021+2022+2023}\)
\(\dfrac{2022}{2023}\) > \(\dfrac{2022}{2021+2022+2023}\)
Cộng vế với vế ta có: P = \(\dfrac{2020}{2021}\) + \(\dfrac{2021}{2022}\) + \(\dfrac{2022}{2023}\) > \(\dfrac{2020+2021+2022}{2021+2022+2023}\) = Q

Ta có: \(6xy+4x+15y+18=0\\ \Leftrightarrow\left(6xy+15y\right)+\left(4x+18\right)=0\\ \Leftrightarrow3y\left(2x+5\right)+2\left(2x+6\right)=0\Leftrightarrow3y\left(2x+5\right)+2\left(2x+5\right)+2=0\\ \Leftrightarrow\left(2x+5\right)\left(3y+2\right)=-2\)
Vì \(x,y\inℤ\) nên \(2x+5\inℤ;3y+2\inℤ\)
\(\Rightarrow\left(2x+5;3y+2\right)\inƯ\left(-2\right)\\\Rightarrow\left(2x+5;3y+2\right)\in \left\{\pm1;\pm2\right\}\)
Ta có bảng sau:
| \(2x+5\) | \(1\) | \(2\) | \(-1\) | \(-2\) |
| \(3y+2\) | \(2\) | \(1\) | \(-2\) | \(-1\) |
| \(x\) | \(\dfrac{8}{11}\) | \(\dfrac{1}{11}\) | \(-\dfrac{8}{11}\) | \(-\dfrac{1}{11}\) |
| \(y\) | \(-\dfrac{1}{11}\) | \(\dfrac{4}{11}\) | \(\dfrac{1}{11}\) | \(-\dfrac{4}{11}\) |
\(\Rightarrow\left(x;y\right)\in\left\{\left(\dfrac{8}{11};-\dfrac{1}{11}\right);\left(\dfrac{1}{11};\dfrac{4}{11}\right);\left(-\dfrac{8}{11};\dfrac{1}{11}\right);\left(-\dfrac{1}{11};-\dfrac{4}{11}\right)\right\}\)(Loại)
Vậy không có nghiệm \(x,y\inℤ\)

\(-\dfrac{2}{7}+\dfrac{5}{12}\cdot\dfrac{18}{35}\)
\(=\dfrac{-2}{7}+\dfrac{18}{12}\cdot\dfrac{5}{35}\)
\(=-\dfrac{2}{7}+\dfrac{3}{2}\cdot\dfrac{1}{7}=\dfrac{-2}{7}+\dfrac{3}{14}=\dfrac{-4+3}{14}=-\dfrac{1}{14}\)

\(\dfrac{x}{3}-\dfrac{2}{y}=\dfrac{1}{5}\)
=>\(\dfrac{xy-6}{3y}=\dfrac{1}{5}\)
=>5(xy-6)=3y
=>5xy-30=3y
=>5xy-3y=30
=>y(5x-3)=30
mà 5x-3>=-3 và y>=0(vì x và y là số tự nhiên)
nên \(\left(5x-3\right)\cdot y=30\cdot1=15\cdot2=10\cdot3=6\cdot5=5\cdot6=3\cdot10=2\cdot15=1\cdot30\)
=>\(\left(x;y\right)\in\left\{\left(\dfrac{33}{5};1\right);\left(\dfrac{18}{5};2\right);\left(\dfrac{13}{5};3\right);\left(\dfrac{9}{5};5\right);\left(\dfrac{8}{5};6\right);\left(\dfrac{6}{5};10\right);\left(1;15\right);\left(\dfrac{4}{5};30\right)\right\}\)
mà x,y là các số tự nhiên
nên \(\left(x;y\right)\in\left(1;15\right)\)

\(\dfrac{1}{2}x+\dfrac{2}{3}x-1=-3\dfrac{1}{3}\)
=>\(x\left(\dfrac{1}{2}+\dfrac{2}{3}\right)=-\dfrac{10}{3}+1\)
=>\(x\cdot\dfrac{7}{6}=\dfrac{-7}{3}\)
=>\(x=-\dfrac{7}{3}:\dfrac{7}{6}=-\dfrac{7}{3}\cdot\dfrac{6}{7}=-2\)

\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{n^2}< \dfrac{1}{n\left(n-1\right)}=\dfrac{1}{n-1}-\dfrac{1}{n}\)
Do đó: \(C=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
=>\(C< 1-\dfrac{1}{n}< 1\)

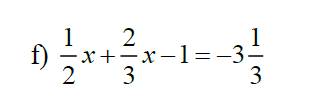
Bài 8:
\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)
\(=\dfrac{1}{3}-\dfrac{1}{99}=\dfrac{33}{99}-\dfrac{1}{99}=\dfrac{32}{99}\)
Bài 6:
a: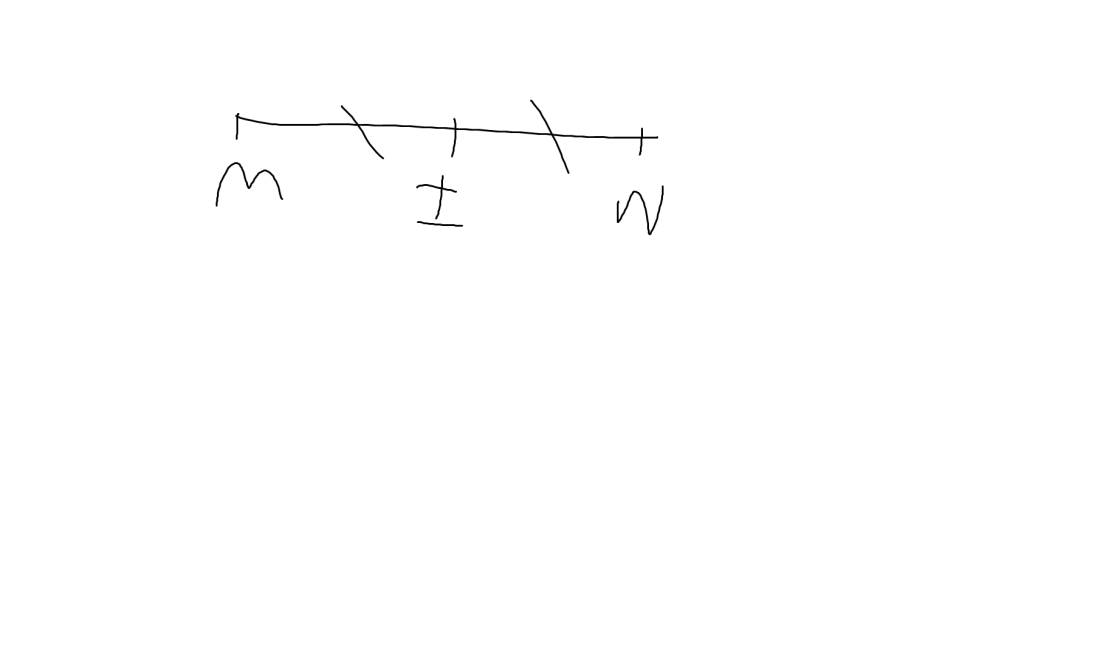
b: I là trung điểm của MN
=>\(MI=\dfrac{MN}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)