a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=90^0-60^0=30^0\)

b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

BA=BH

Do đó: ΔBAE=ΔBHE

=>\(\widehat{ABE}=\widehat{HBẺ}\)

=>BE là phân giác của góc ABC

c: Xét ΔBKC có

KH,CA là các đường cao

KH cắt CA tại E

Do đó: E là trực tâm của ΔBKC

=>BE\(\perp\)KC

a) Tính góc C: Vì tam giác ABC vuông tại A và góc B = 60 độ, ta có góc C = 90 - 60 = 30 độ.

b) Chứng minh BE là tia phân giác của góc B: Gọi I là trung điểm của AB, vậy BI là đoạn thẳng phân giác của góc B. Ta có HB = AB và BI là đoạn thẳng phân giác của góc B, do đó tam giác BHI là tam giác đều. Do đó, góc BHI = 60 độ. Mà góc HBE là góc ngoài của tam giác BHI, vậy góc HBE = 60 độ. Vậy, BE là tia phân giác của góc B.

c) Chứng minh rằng BE vuông góc với KC: Ta có:

• Tam giác ABC vuông tại A.
• Tam giác BHI đều. Vậy ta có:
• AH là đường cao của tam giác ABC, vì vậy HK là đường cao của tam giác BHI.
• BK là cạnh của tam giác BHI. Vậy tam giác BKH là tam giác vuông tại K.

Vậy góc HKB = 90 độ.

Nhưng ta đã chứng minh BE là tia phân giác của góc B, vậy góc HBE = góc EBK.

Vậy ta có: góc EBK + góc HKB = góc HBE + góc HKB = 60 + 90 = 150 độ.

Nhưng tổng các góc trong tam giác BKH là 180 độ, vậy góc EBK + góc HKB = 180 độ.

Từ đó suy ra góc EBK = 30 độ.

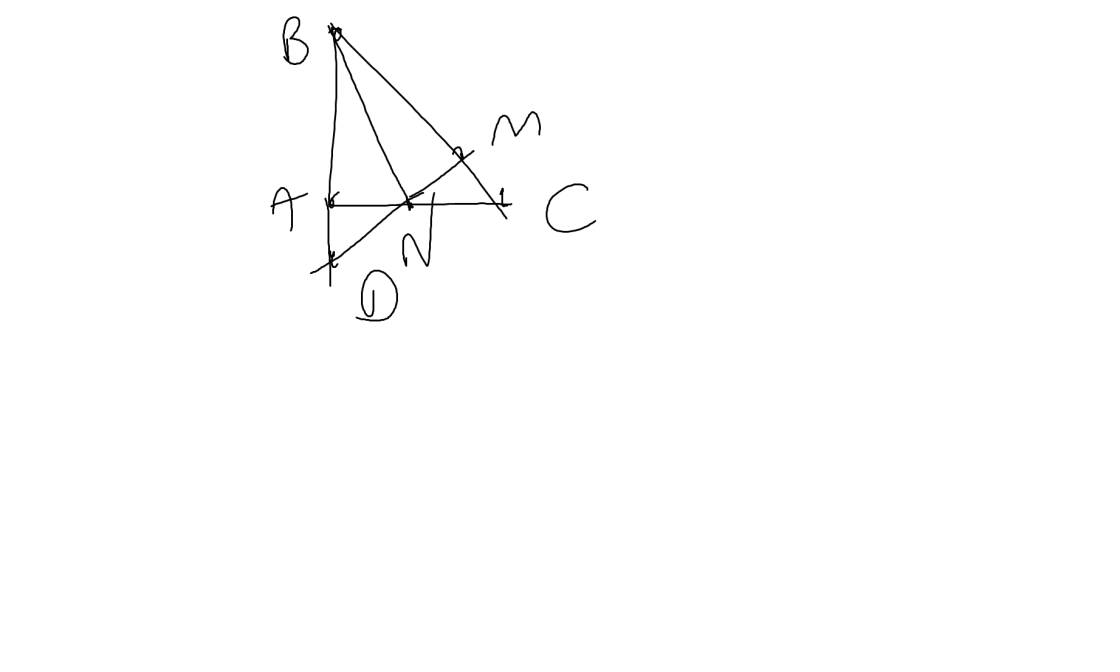
Sửa đề; BA=BM

Xét ΔBAN và ΔBMN có

BA=BM

\(\widehat{ABN}=\widehat{MBN}\)

BN chung

Do đó: ΔBAN=ΔBMN

=>\(\widehat{BAN}=\widehat{BMN}\)

=>\(\widehat{BMN}=90^0\)

=>NM\(\perp\)BC

Xét ΔNAD vuông tại A và ΔNMC vuông tại M có

NA=NM(ΔBAN=ΔBMN)

\(\widehat{AND}=\widehat{MNC}\)(hai góc đối đỉnh)

Do đó: ΔNAD=ΔNMC

=>AD=MC

BC=BM+MC

mà BA=BM và MC=AD

nên BC=BA+AD

\(\infty\) j thế kia?

Bài 1: (Nhận biết )

Ta có: \(\dfrac{2}{5};\dfrac{2}{3}< 1\) ( tử bé hơn mẫu ) và \(\dfrac{2}{5}< \dfrac{2}{3}\) 

\(\dfrac{8}{7};\dfrac{11}{7}>1\) ( tử lớn hơn mẫu ) và \(\dfrac{8}{7}< \dfrac{11}{7}\)

\(->\dfrac{2}{5}< \dfrac{2}{3}< 1< \dfrac{8}{7}< \dfrac{11}{7}\)

___

Sắp xếp theo thứ tự từ bé đến lớn: \(\dfrac{2}{5};\dfrac{2}{3};1;\dfrac{8}{7};\dfrac{11}{7}\)

Bài 2:

a. \(\dfrac{4}{15}\times?=\dfrac{2}{15}\)

\(=>?=\dfrac{2}{15}:\dfrac{4}{15}=\dfrac{2}{15}\times\dfrac{15}{4}\)

\(=>?=\dfrac{1}{2}\)

b. \(\dfrac{7}{24}+?=2-\dfrac{1}{4}\)

\(=>\dfrac{7}{24}+?=\dfrac{7}{4}\)

\(=>?=\dfrac{7}{4}-\dfrac{7}{24}=\dfrac{42}{24}-\dfrac{7}{24}\)

\(=>?=\dfrac{35}{24}\)

`#NqHahh`

Chọn C. \(\dfrac{3}{8}\)

Vì 3 < 8 nên \(\dfrac{3}{8}< 1\)

C. 3/8.

Đổi 75cm trên thực tế = 2,5 đơn vị trên mặt phẳng toạ độ

Gọi điểm cách điểm O 2,5 đơn vị và thuộc đường elip là M => M(2,5;y)

Thay toạ độ điểm M vào pt đường elip, ta có: (2,5)²/16 + y²/4 = 1 

=> y²/4 = 39/64

=> y = căn39/4 ≈ 1,56 

Chiều cao h của ô thoáng là: 1,56 . 30 = 46,8 (cm)

A. 7/5.

A. 7/5.