Đặt \(P=x^3+y^3+z^3-3xyz\)

\(=x^3+\left(y+z\right)^3-3yz\left(y+z\right)-3xyz\)

\(=\left(x+y+z\right)\left[x^2-x\left(y+z\right)+\left(y+z\right)^2\right]-3yz\left(x+y+z\right)\)

\(=3\left(x^2+y^2+z^2+2yz-xy-xz\right)-9yz\)

\(=3\left(x^2+y^2+z^2-xy-yz-zx\right)\)

\(=3\left[\left(x+y+z\right)^2-3\left(xy+yz+zx\right)\right]\)

\(=3\left[9-3\left(xy+yz+zx\right)\right]\)

Do \(0\le x,y,z\le2\Rightarrow\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge0\)

\(\Rightarrow xyz+\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge0\)

\(\Rightarrow2\left(xy+yz+zx\right)-4\left(x+y+z\right)+8\ge0\)

\(\Rightarrow2\left(xy+yz+zx\right)\ge4.3-8=4\)

\(\Rightarrow xy+yz+zx\ge2\)

\(\Rightarrow P\le3.\left[9-3.2\right]=9\)

\(P_{max}=9\) khi \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị của chúng

\(x^3-8y^3+7=0\\ =>x^3-\left(2y\right)^3=-7\\ =>\left(x-2y\right)\left(x^2+2xy+4y^2\right)=-7\)

Vì x,y nguyên nên: 

TH1: \(\left\{{}\begin{matrix}x-2y=1\\x^2+2xy+4y^2=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=1\\\left(x-2y\right)^2+6xy=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=1\\xy=-\dfrac{4}{3}\end{matrix}\right.\) (loại vì x,y nguyên => xy nguyên)  

\(TH2:\left\{{}\begin{matrix}x-2y=7\\x^2+2xy+4y^2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=7\\\left(x-2y\right)^2+6xy=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=7\\xy=-\dfrac{25}{3}\end{matrix}\right.\) (loại vì x,y nguyên => xy nguyên) 

TH3: \(\left\{{}\begin{matrix}x-2y=-1\\x^2+2xy+4y^2=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=-1\\\left(x-2y\right)^2+6xy=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=-1\\xy=1\end{matrix}\right.\) 

\(\Leftrightarrow\left\{{}\begin{matrix}x=2y-1\\\left(2y-1\right)y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-1\\2y^2-y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-1\\\left(y-1\right)\left(2y+1\right)=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\cdot1-1=1\\\left[{}\begin{matrix}y=1\left(tm\right)\\y=-\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\) 

TH4: \(\left\{{}\begin{matrix}x-2y=-7\\x^2+2xy+4y^2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=-7\\\left(x-2y\right)^2+6xy=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y=-7\\xy=-8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=2y-7\\\left(2y-7\right)y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-7\\2y^2-7y+8=0\end{matrix}\right.\Leftrightarrow x,y\in\varnothing\)

Vậy: x = 1 và y = 1 

giúp mik vs gấp lắm r

1)

\(a,-9-9\left(-5\right)\\ =-9+45\\ =36\\ b,-5-\left(-12\right)\\ =-5+12\\ =7\)

2) 

\(A=-7x+3-15x+8\\ =\left(-7x-15x\right)+\left(3+8\right)\\ =x\cdot\left(-7-15\right)+11\\ =-22x+11\)

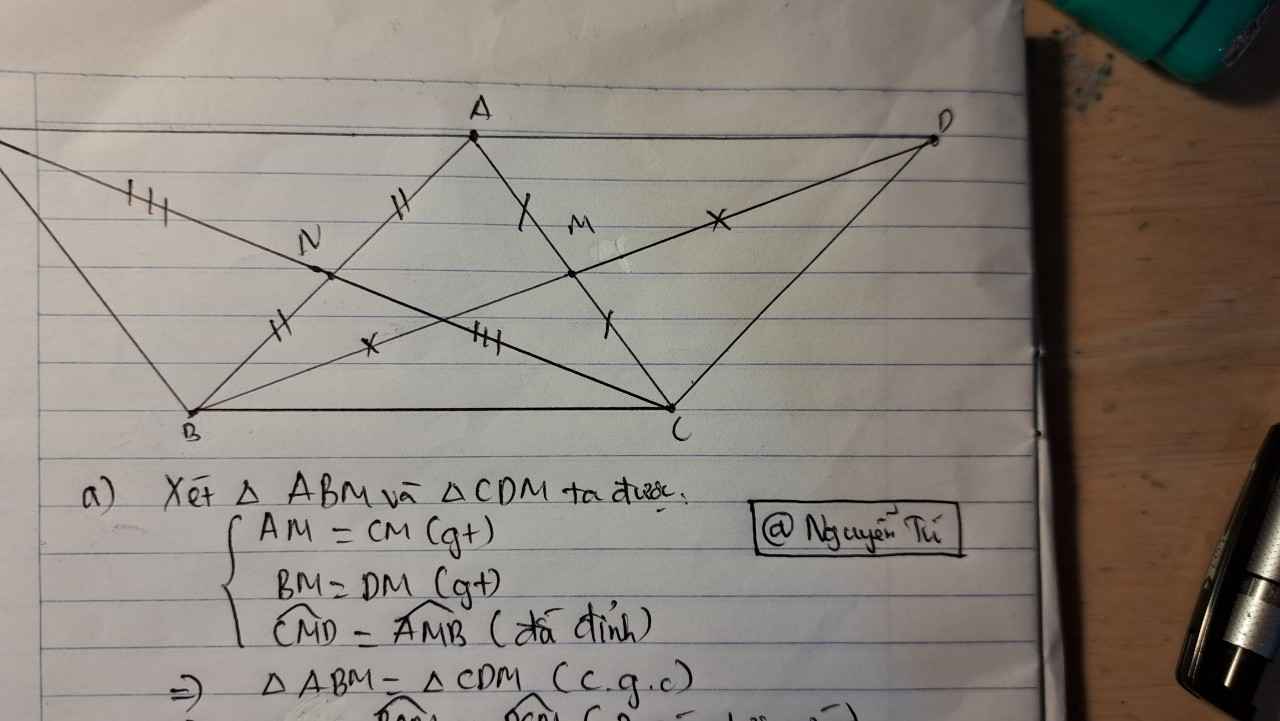
a: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD
=>\(\widehat{MAB}=\widehat{MCD}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CD
ΔMAB=ΔMCD
=>AB=CD

b: Xét ΔNBC và ΔNAE có

NB=NA

\(\widehat{BNC}=\widehat{ANE}\)(hai góc đối đỉnh)

NC=NE

Do đó: ΔNBC=ΔNAE

=>\(\widehat{NBC}=\widehat{NAE}\)

=>BC//AE 

ΔNBC=ΔNAE
=>BC=AE

Xét ΔMBC và ΔMDA có

MB=MD
\(\widehat{BMC}=\widehat{DMA}\)(hai góc đối đỉnh)

MC=MA

Do đó: ΔMBC=ΔMDA

=>\(\widehat{MBC}=\widehat{MDA}\)

mà hai góc này là hai góc ở vị trí so le trong

nên BC//DA

ΔMBC=ΔMDA
=>BC=DA

Ta có: BC//DA
BC//AE

mà AD,AE có điểm chung là A

nên D,A,E thẳng hàng

mà AD=AE(=BC)

nên A là trung điểm của DE

\(M=x^2-4x+8\\ =\left(x^2-4x+4\right)+4\\ =\left(x-2\right)^2+4\)

Ta có:

`(x-2)^2>=0` với mọi x

`=>M=(x-2)^2+4>=4` với mọi x

Dấu "=" xảy ra: `x-2=0<=>x=2` 

Vậy: ... 

\(\left(x^2y^2+2x^2y+x^2\right)\left(x^2+2x-2\right)=\left(xy+x\right)^2\left(x^2+2x-2\right)\)

Do \(\left(xy+x\right)^2\) chính phương với mọi x;y nguyên nên biểu thức đã cho chính phương khi \(x^2+2x-2\) là SCP

\(\Rightarrow x^2+2x-2=k^2\)

\(\Rightarrow\left(x+1\right)^2-k^2=3\)

\(\Rightarrow\left(x+1-k\right)\left(x+1+k\right)=3\)

Pt ước số cơ bản, dễ dàng giải ra \(x=\left\{-3;1\right\}\)

Vậy \(\left(x;y\right)=\left(-3;k\right);\left(1;k\right)\) với k là số nguyên bất kì

Ta có: 

\(y^3+2y^2+y+4=\left(y+2\right)^3-\left(4y^2+11y+4\right)\)

Do y là số tự nhiên \(\Rightarrow4y^2+11y+4>0\Rightarrow\left(y+2\right)^3>y^3+2y^2+y+4\)

Đồng thời cũng do y tự nhiên \(\Rightarrow2y^2+y+4>0\Rightarrow y^3+2y^2+y+4>y^3\)

\(\Rightarrow y^3< y^3+2y^2+y+4< \left(y+2\right)^3\)

\(\Rightarrow y^3+2y^2+y+4\) là lập phương của 1 số tự nhiên khi và chỉ khi:

\(y^3+2y^2+y+4=\left(y+1\right)^3\)

\(\Leftrightarrow y^2+2y-3=0\Rightarrow y=1\)

\(\Rightarrow x^3=8\Rightarrow x=2\)

a.

\(=\left(x^2+2xy+y^2\right)-9\)

\(=\left(x+y\right)^2-3^2\)

\(=\left(x+y-3\right)\left(x+y+3\right)\)

b.

\(=\left(x^2+4xy+4y^2\right)-4\)

\(=\left(x+2y\right)^2-2^2\)

\(=\left(x+2y-2\right)\left(x+2y+2\right)\)

c.

\(=\left(x^2+6xy+9y^2\right)-16\)

\(=\left(x+3y\right)^2-4^2\)

\(=\left(x+3y-4\right)\left(x+3y+4\right)\)

d.

\(=\left(x^2+8xy+16y^2\right)-9\)

\(=\left(x+4y\right)^2-3^2\)

\(=\left(x+4y-3\right)\left(x+4y+3\right)\)

em c.on ạ

Bài 2:

a: Xét ΔADF vuông tại D và ΔAHF vuông tại H có

AF chung

\(\widehat{DAF}=\widehat{HAF}\)

Do đó: ΔADF=ΔAHF

=>AD=AH

=>AH=a

b: AH=AD

mà AD=AB

nên AH=AB

Xét ΔAHK vuông tại H và ΔABK vuông tại B có

AK chung

AH=AB

Do đó: ΔAHK=ΔABK

=>\(\widehat{KAB}=\widehat{KAH}\)

=>AK là phân giác của góc HAB

\(\widehat{KAF}=\widehat{KAH}+\widehat{FAH}=\dfrac{1}{2}\left(\widehat{BAH}+\widehat{DAH}\right)=\dfrac{1}{2}\cdot90^0=45^0\)

sai