Cho tam giác ABC cân tại A lấy điểm D thuộc cạnh AC và điểm E thuộc cạnh AB Sao cho AD = AE Chứng minh AB = AC
a.chứng minh adb=aec
b.gọi i là giao điểm của bd và ce tam giác ibc là tam giác gì vì sao
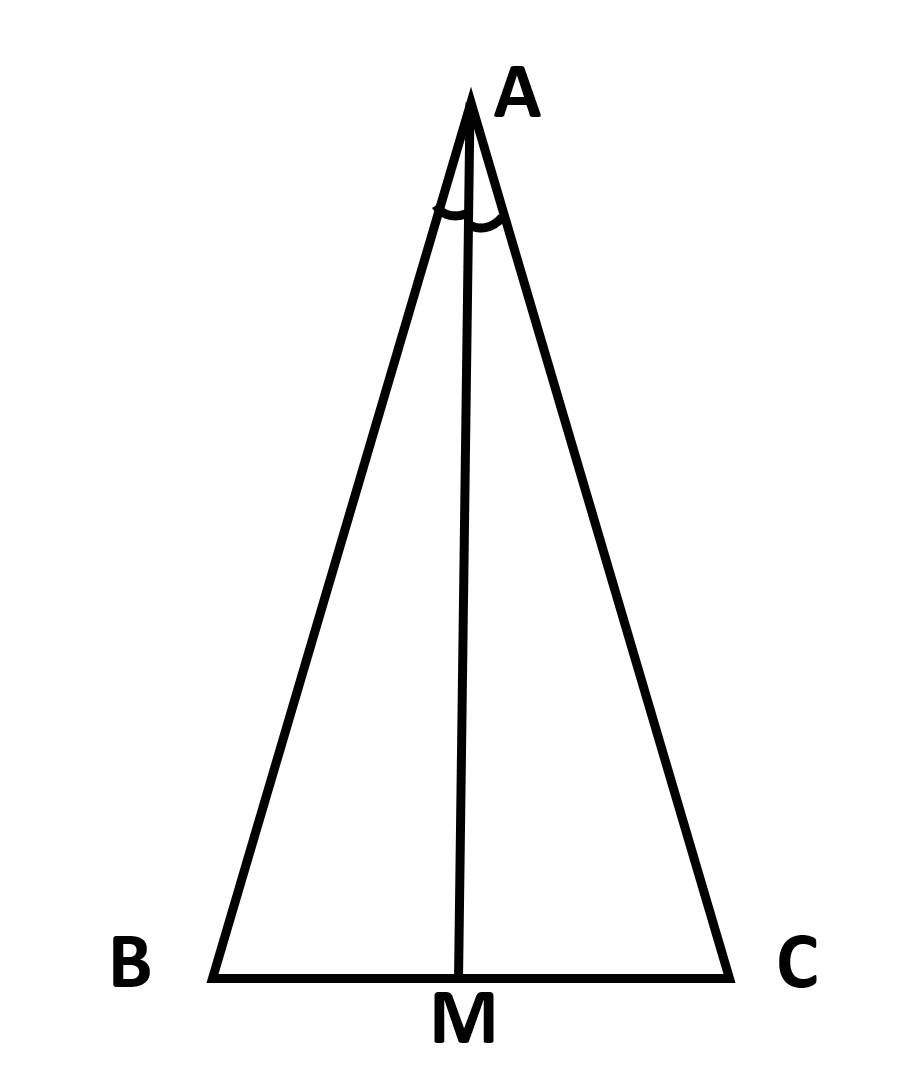
c. Gọi m là trung điểm của bc chứng minh a,i,m thẳng hàng
Giúp tớ với đi làm ơn


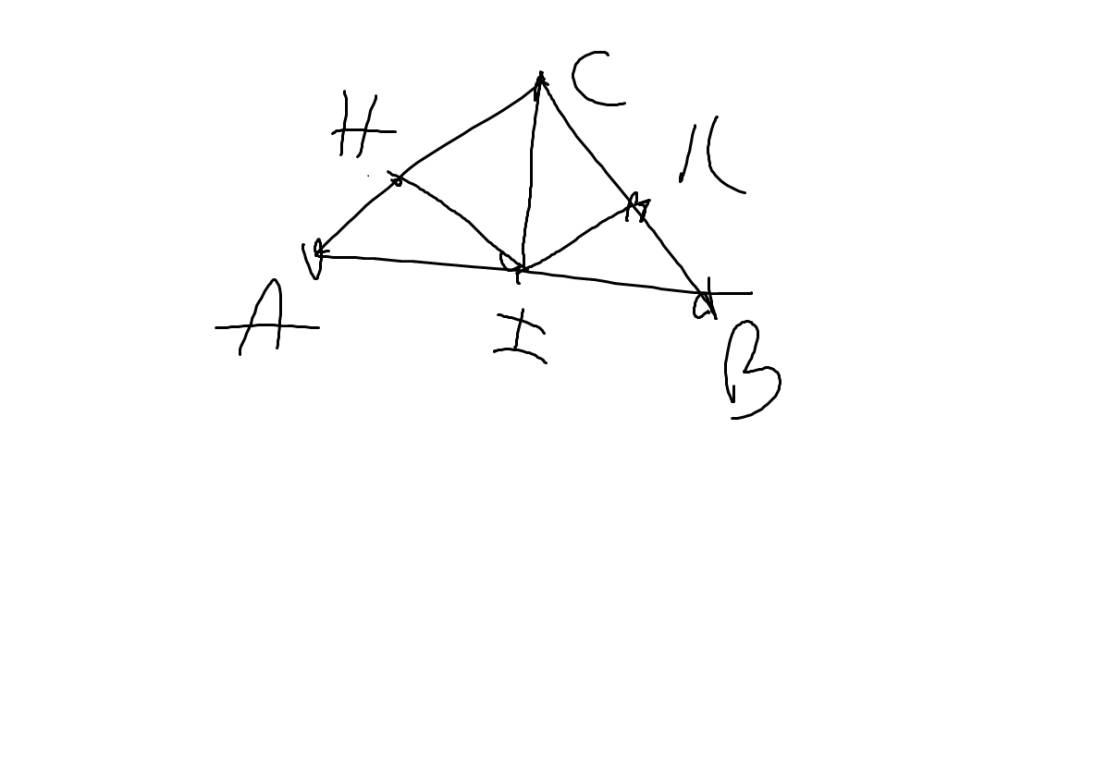

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
=>\(\widehat{ABD}=\widehat{ACE}\)
Ta có: \(\widehat{ABD}+\widehat{CBD}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{ABD}=\widehat{ACE}\) và \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{CBD}=\widehat{ECB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
c: ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: IB=IC
=>I nằm trên đường trung trực của BC(2)
ta có: MB=MC
=>M nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,I,M thẳng hàng
trả lời đi