Để ước tính cân nặng lý tưởng W (kg) của một người trưởng thành có chiều cao h (cm), người ta ng dùng công thức sau: W = 0,9(h – 152) + 47,75 + a với a = 2,25 nếu người đó là nam và a = - 2,25 nếu người nữ.
Tính cân nặng lí tưởng của một người đàn ông cao 174,5 cm và một người phụ nữ cao 165,5 cm theo công thức này.
Một người cao hơn 1,65 m có cân nặng lí tưởng tính theo công thức này là 60,8 kg. Hãy cho biết người đó là nam hay nữ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(x^2+y^2=2\)
\(\Rightarrow0\le x\le\sqrt{2}\)
\(0\le y\le\sqrt{2}\)(1)
Lại có:
\(P=x+3y\)
\(\Rightarrow3y\ge0\) (1)
Để P nhỏ nhất thì x hoặc 3y đạt giá trị nhỏ nhất vì x và 3y đều lớn hơn 0.
Xét trường hợp x nhỏ nhất:
\(x\ge0\) dấu bằng xảy ra \(\Leftrightarrow x=0\Rightarrow y=\sqrt{2}\)
\(\Rightarrow P=3\sqrt{2}\)
Xét trường hợp y nhỏ nhất.
\(y\ge0\) dấu bằng xảy ra \(\Leftrightarrow y=0\Rightarrow x=\sqrt{2}\)
\(\Rightarrow P=\sqrt{2}\)
Vậy giá trị nhỏ nhất của P tại \(\left(x,y\right)=\left(\sqrt{2},0\right)\)

a: \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+b^2d^2+2acbd+a^2d^2+b^2c^2-2adbc\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: \(x^2+y^2=\dfrac{1}{2}\left(2x^2+2y^2\right)\)
\(=\dfrac{1}{2}\left(x^2+2xy+y^2+x^2-2xy+y^2\right)\)
\(=\dfrac{1}{2}\left[\left(x+y\right)^2+\left(x-y\right)^2\right]=\dfrac{1}{2}\left[4+\left(x-y\right)^2\right]>=\dfrac{1}{2}\cdot4=2\)
Dấu '=' xảy ra khi x=y=1

Lời giải:
a.
Vì $BE, CF$ là đường cao của tam giác $ABC$ nên $\widehat{BFC}=\widehat{BEC}=90^0$
Tứ giác $BCEF$ có $\widehat{BFC}=\widehat{BEC}$ và cùng nhìn cạnh $BC$ nên $BCEF$ là tứ giác nội tiếp.
b.
Xét tam giác $BFH$ và $CFA$ có:
$\widehat{BFH}=\widehat{CFA}=90^0$
$\widehat{FBH}=\widehat{FBE}=\widehat{FCE}=\widehat{FCA}$ (do $BCEF$ là tgnt)
$\Rightarrow \triangle BFH\sim \triangle CFA$ (g.g)
$\Rightarrow \frac{BF}{CF}=\frac{BH}{CA}$
$\Rightarrow BF.CA=BH.CF$
c.
Kéo dài $AO$ cắt $(O)$ tại $M$ thì $O$ là trung điểm $AM$.
$K$ là trung điểm $BC$ nên $OK\perp BC$, AH\perp BC$ (do $H$ là trực tâm)
$\Rightarrow OK\parallel AH$
Có: $\widehat{ABM}=\widehat{ACM}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow AB\perp BM, AC\perp CM$
Mà $CH\perp AB, BH\perp AC$ nên $BM\parallel CH, CM\parallel BH$
$\Rightarrow BHCM$ là hình bình hành (tứ giác có 2 cặp cạnh đối song song)
$\Rightarrow HM, BC$ cắt nhau tại trung điểm $K$ của $BC$
$\Rightarrow H,K,M$ thẳng hàng.
Tam giác $AHM$, áp dụng định lý Talet có:
$\frac{OK}{AH}=\frac{OM}{AM}=\frac{1}{2}$

a: 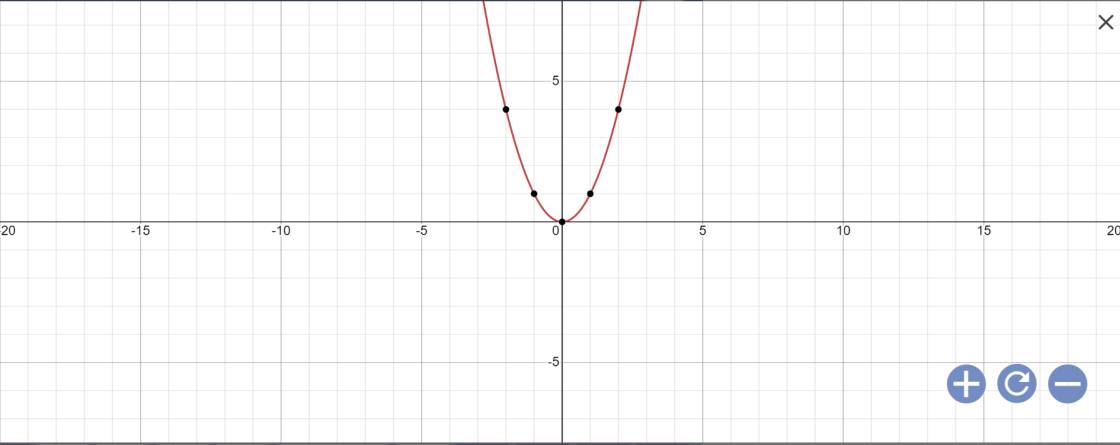
b: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x+6\)
=>\(x^2-\left(m-2\right)x-6=0\)
\(a\cdot c=1\cdot\left(-6\right)=-6< 0\)
=>(P) luôn cắt (d) tại hai điểm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m-2\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)
\(x_2^2-x_1x_2+\left(m-2\right)x_1=16\)
=>\(x_2^2+x_1\left(x_1+x_2\right)-x_1x_2=16\)
=>\(x_2^2+x_1^2=16\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=16\)
=>\(\left(m-2\right)^2-2\cdot\left(-6\right)=16\)
=>\(\left(m-2\right)^2=4\)
=>\(\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)

a: Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=90^0+90^0=180^0\)
nên AMHN là tứ giác nội tiếp
b: Xét tứ giác BNMC có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp
=>\(\widehat{BNM}+\widehat{BCM}=180^0\)
mà \(\widehat{BNM}+\widehat{ANM}=180^0\)(hai góc kề bù)
nên \(\widehat{ANM}=\widehat{ACB}\)

Thay y=-2 vào (d), ta được:
\(\dfrac{1}{2}x+2=-2\)
=>\(\dfrac{x}{2}=-4\)
=>x=-8
Thay x=-8 và y=-2 vào y=ax+b, ta được:
\(a\cdot\left(-8\right)+b=-2\)
=>-8a+b=-2
=>8a-b=2(1)
Thay x=2 và y=-3 vào y=ax+b, ta được:
\(a\cdot2+b=-3\)
=>2a+b=-3(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}8a-b=2\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10a=-1\\8a-b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-\dfrac{1}{10}\\b=8a-2=-\dfrac{8}{10}-2=-\dfrac{28}{10}=-\dfrac{14}{5}\end{matrix}\right.\)
Vậy: (d'): \(y=-\dfrac{1}{10}x-\dfrac{14}{5}\)
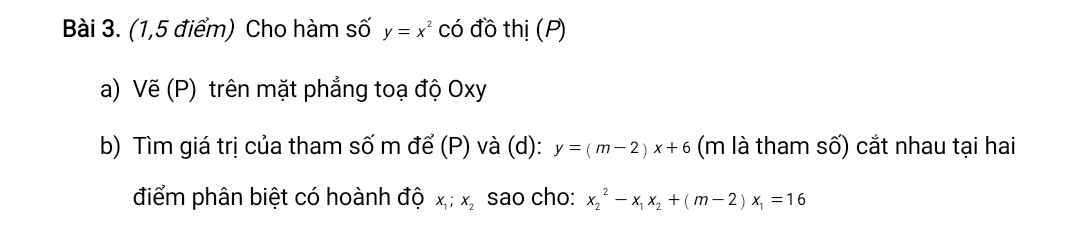
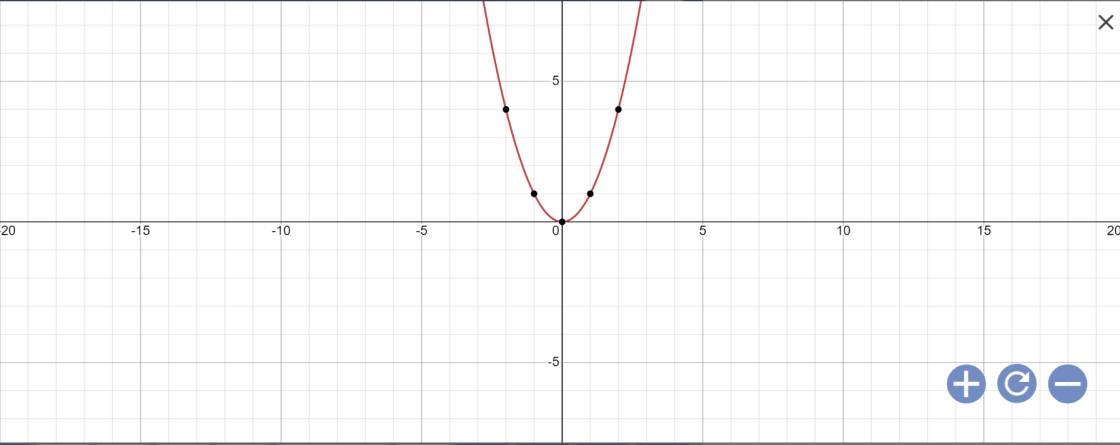

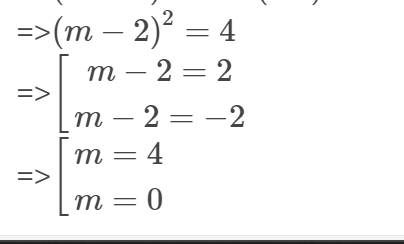
Cân nặng lí tưởng của người đàn ông cao 174,5cm là:
W=0,9(174,5-152)+47,75+2,25=0,9*22,5+50=70,25(kg)
Cân nặng lí tưởng của người phụ nữ cao 165,5cm là:
\(W=0,9\cdot\left(165,5-152\right)+47,75-2,25=57,65\left(kg\right)\)
b: Theo đề, ta có:
\(0,9\left(h-152\right)+47,75+a=60,8\)
=>\(\left[{}\begin{matrix}0,9\left(h-152\right)+47,75+2,25=60,8\\0,9\left(h-152\right)+47,75-2,25=60,8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}0,9\left(h-152\right)=10,8\\0,9\left(h-152\right)=15,3\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}h-152=12\\h-152=15,3:0,9=17\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}h=164\left(loại\right)\\h=169\left(nhận\right)\end{matrix}\right.\)
Vậy: h=169(cm)=1,69(m)
=>Người đó là nữ
a)
Cân nặng lí tưởng của người đàn ông cao 174,5 cm là:
W = 0,9(174,5-152)+47,75+2,25=70,25(kg)
Cân nặng lí tưởng của người phụ nữ cao 165,5 cm là:
W = 0,9(165,5-152)+47,75-2,25=57,65 (kg)
b)Ta có: h>165
=> h-152>13
=> 0,9(h-152)>11,7
=> 0,9(h-152)+47,75+a>59,45+a
=> W>59,45+a
=> 60,8>59,45+a ( Theo đề: W=60,8 )
=> 1,35 > a
a chỉ có thể xảy ra hoặc 2,25 hoặc -2,25
Trong trường hợp này a chỉ có thể -2,25
Hay người đó là nữ