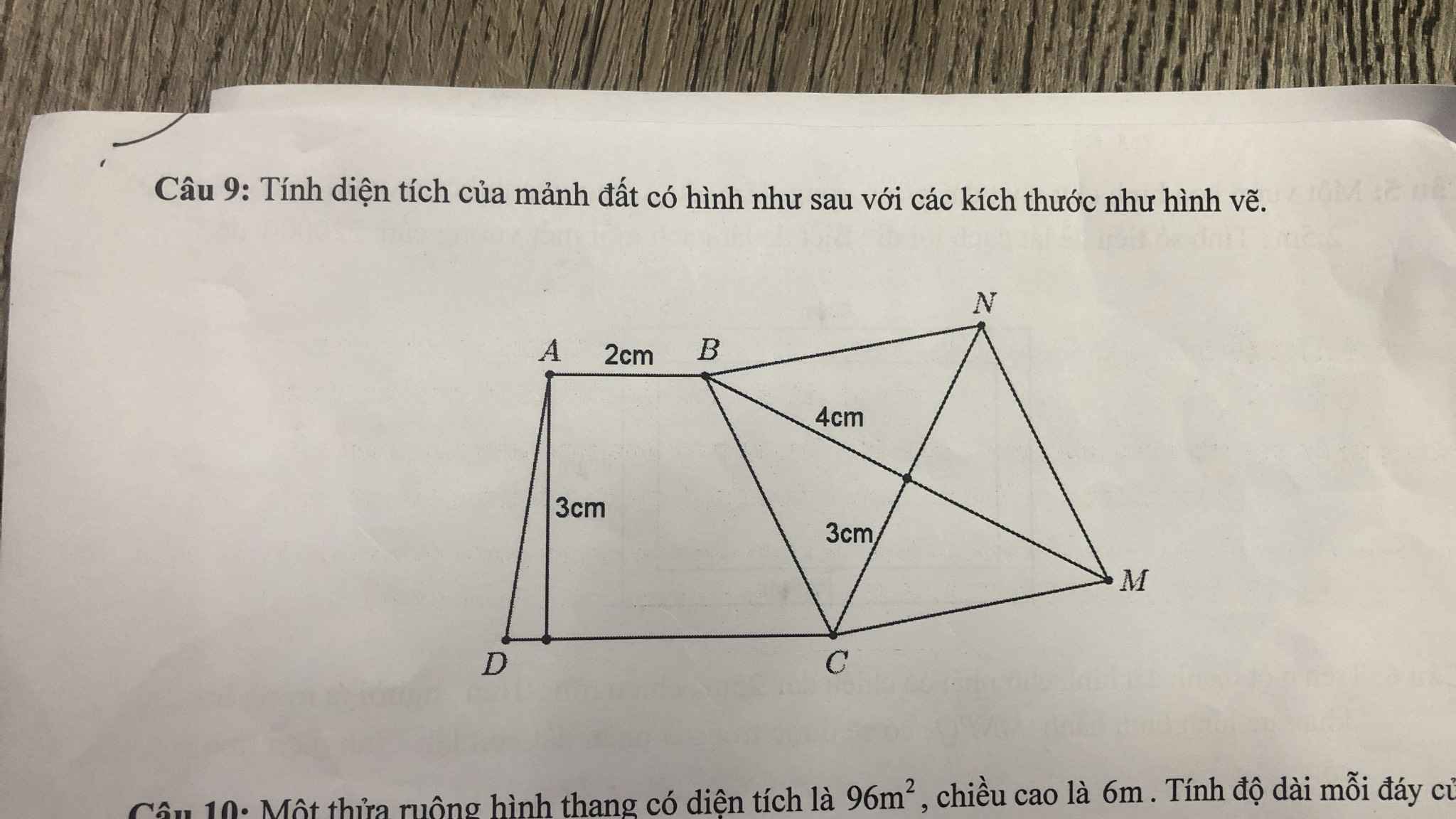
mn giúp mik vs ạ !
mn giúp mik vs ạ !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HY
Nguyễn Mai Phương ơi câu hỏi đấy ở trong sách 250 bài toán chọn lọc lớp 4 của thầy trần nhật minh đó
0

HN
0


TP
0