\(A\) = \(\dfrac{1}{10}\)+\(\dfrac{1}{11}\)+\(\dfrac{1}{12}\)+\(\dfrac{1}{13}\)+...+\(\dfrac{1}{69}\)+\(\dfrac{1}{70}\) chứng tỏ A < \(\dfrac{51}{20}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Lượng muối có trong mỗi lít nước biển = 1.026Kg x 2,5 % =0.02565kg
Số lít nước biển cần để có 513Kg muối là:
L= 513/ 0.02565 = 20.000 lít
Đáp số: 20.000 lít nước biển

e; (1\(\dfrac{1}{3}\) - 25%\(x\) - \(\dfrac{5}{12}\)) - 2\(x\) = 1,6 : \(\dfrac{3}{5}\)
\(\dfrac{4}{3}\) - 0,25\(x\) - \(\dfrac{5}{12}\) - 2\(x\) = \(\dfrac{8}{3}\)
(\(\dfrac{4}{3}\) - \(\dfrac{5}{12}\)) - (0,25\(x\) + 2\(x\)) = \(\dfrac{8}{3}\)
\(\dfrac{11}{12}\) - 2,25\(x\) = \(\dfrac{8}{3}\)
2,25\(x\) = \(\dfrac{11}{12}\) - \(\dfrac{8}{3}\)
2,25\(x\) = - \(\dfrac{7}{4}\)
\(x\) = - \(\dfrac{7}{4}\) : 2,25
\(x\) = - \(\dfrac{7}{9}\)
Vậy \(x=-\dfrac{7}{9}\)
f; \(\dfrac{1}{2}\).(\(x-\dfrac{2}{3}\)) - \(\dfrac{1}{3}\) (2\(x\) - 3) = \(x\)
\(\dfrac{1}{2}\)\(x\) - \(\dfrac{1}{3}\) - \(\dfrac{2}{3}x\) + 1= \(x\)
(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))\(x\) + (1 - \(\dfrac{1}{3}\)) = \(x\)
- \(\dfrac{1}{6}\)\(x\) + \(\dfrac{2}{3}\) = \(x\)
\(x\) + \(\dfrac{1}{6}\)\(x\) = \(\dfrac{2}{3}\)
\(\dfrac{7}{6}\)\(x\) = \(\dfrac{2}{3}\)
\(x\) = \(\dfrac{2}{3}\) : \(\dfrac{7}{6}\)
\(x\) = \(\dfrac{4}{7}\)
Vậy \(x\) = \(\dfrac{4}{7}\)

\(A=\dfrac{1}{5}+\dfrac{3}{35}+\dfrac{1}{21}+\dfrac{1}{33}+\dfrac{3}{143}+\dfrac{1}{65}\)
\(=\left(\dfrac{1}{5}+\dfrac{1}{21}+\dfrac{3}{35}\right)+\left(\dfrac{1}{33}+\dfrac{1}{143}+\dfrac{1}{65}\right)\)
\(=\dfrac{21+5+9}{105}+\dfrac{13+3}{429}+\dfrac{1}{65}\)
\(=\dfrac{1}{3}+\dfrac{1}{65}+\dfrac{16}{429}\)
\(=\dfrac{276}{715}\)

a: Số tiền ban đầu bác Hai gửi vào là:
\(7,2:7,2\cdot100=100\left(triệuđồng\right)\)
b: Sau năm thứ nhất thì tổng số tiền bác Hai nhận được là:
100+7,2=107,2(triệu đồng)
Sau 2 năm thì số tiền bác Hai nhận được là:
\(107,2\cdot\left(1+7,2\%\right)=114,9184\)(triệu đồng)

a; 5\(x\) - 1\(\dfrac{1}{4}\) = \(\dfrac{5}{6}\)
5\(x\) - \(\dfrac{5}{4}\) = \(\dfrac{5}{6}\)
5\(x\) = \(\dfrac{5}{6}\) + \(\dfrac{5}{4}\)
5\(x\) = \(\dfrac{25}{12}\)
\(x\) = \(\dfrac{25}{12}\) : 5
\(x\) = \(\dfrac{5}{12}\)
Vậy \(x=\dfrac{5}{12}\)
b; \(\dfrac{5}{8}\) + \(\dfrac{1}{2}\) = \(\dfrac{12}{x}\)
\(\dfrac{9}{8}\) = \(\dfrac{12}{x}\)
\(x\) = 12 : \(\dfrac{9}{8}\)
\(x\) = \(\dfrac{32}{3}\)
Vậy \(x=\dfrac{32}{3}\)

a: \(\dfrac{1}{2}+\dfrac{-1}{6}+\dfrac{-1}{12}+\dfrac{-1}{20}+\dfrac{-1}{30}+\dfrac{-1}{42}\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{42}\right)\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{6\cdot7}\right)\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{6}-\dfrac{1}{7}\right)\)
\(=\dfrac{1}{2}-\dfrac{1}{2}+\dfrac{1}{7}=\dfrac{1}{7}\)
b: \(25\%-1\dfrac{1}{2}-\left(-\dfrac{1}{2}\right)^2+0,25:\dfrac{1}{12}\)
\(=0,25-1,5-0,25+0,25\cdot12\)
=3-1,5=1,5

Đây là dạng toán nâng cao chuyên đề phân số, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau.
Giải:
\(\dfrac{7}{10}\)Số học sinh nữ bằng: \(\dfrac{4}{5}\) x \(\dfrac{7}{10}\) = \(\dfrac{14}{25}\) (số học sinh nam)
Số học sinh giỏi bằng: \(\dfrac{3}{5}\) + \(\dfrac{14}{25}\) = \(\dfrac{29}{25}\) (số học sinh nam)
vậy số học sinh nam phải chia hết cho 25
Số học sinh nam là bội của 25
B(25) = {0; 25; 50; 75; 100;..;}
Vì sĩ số của một lớp không thể vượt quá 100 em nên số học sinh nam của lớp 6A là 25 học sinh
Số học sinh lớp 6A bằng: (4 + 5): 5 = \(\dfrac{9}{5}\) (số học sinh nam)
Số học sinh lớp 6A là: 25 x \(\dfrac{9}{5}\) = 45 (học sinh)
Kết luận số học sinh lớp 6A là 45 học sinh.

bạn cho mình xin hình vẽ nha bạn
nhưng mà nhìn các đáp án mình sẽ chọn ngay C rồi, bởi tia Ax và Ox có chung gốc đâu nên ko thể trùng nhau được

Đây là toán nâng cao chuyên đề phân số có quy luật, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp kẹp.
A = \(\dfrac{1}{1^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{5^2}\) + \(\dfrac{1}{7^2}\) + ... + \(\dfrac{1}{99^2}\)
0 < A = \(\dfrac{1}{1^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{5^2}\) + \(\dfrac{1}{7^2}\) + ... + \(\dfrac{1}{99^2}\) = 1 + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{5^2}\) + \(\dfrac{1}{7^2}\) + ... + \(\dfrac{1}{99^2}\)
0 < A < 1
Vậy A không phải là số tự nhiên vì không thể tồn tại một số tự nhiên giữa hai số tự nhiên liến tiếp.
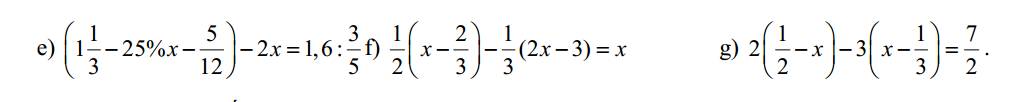 Giúp em với ạ.
Giúp em với ạ.