Tìm nghiệm nguyên: x2 + xy + y2 = x2 y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(F=\left(n-4\right)\left(n+2\right)\left(n+6\right)\)
Với \(n=4;n=-2;n=-6\) thì hiển nhiên F chia hết cho 125. Nhưng do n là số nguyên dương nên ta chỉ chọn \(n=4\)
Nếu F khác 0:
Do F chia hết cho 125 nên F cũng chia hết cho 5. Do 5 là số nguyên tố nên 1 trong 3 số \(n-4,n+2,n+6\) sẽ phải chia hết cho 5.
Nếu số đó là \(n-4\) thì đương nhiên \(n+6=n-4+10⋮5\) và \(n+2=n-4+6⋮̸5\). Vậy F không chia hết cho 125.
Nếu số đó là \(n+6\) thì \(n-4=n+6-10⋮5\) và \(n+2=n+6-4⋮̸5\). Vậy F không chia hết cho 125.
Nếu số đó là \(n+2\) thì \(n-4=n+2-6⋮̸5\) và \(n-4=n+2-6⋮̸5\). Vậy F cũng không chia hết cho 125.
Như vậy số nguyên dương n nhỏ nhất thỏa mãn F chia hết cho 125 là \(n=4\)


\(\left(\sqrt{7}-\sqrt{3}\right)^2+\sqrt{84}\)
\(=10-2\sqrt{21}+2\sqrt{21}\)
= 10
Giải phương trình:
$$ 2\left(x-\sqrt{2 x^2+5 x-3}\right)=1+x(\sqrt{2 x-1}-2 \sqrt{x+3}) \text {. }$$

ĐKXĐ : \(\left\{{}\begin{matrix}2x^2+5x-3\ge0\\2x-1\ge0\\x+3\ge0\end{matrix}\right.\)
Phương trình tương đương : \(2x-2\sqrt{2x^2+5x+3}=1+x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow2x-1-2\sqrt{\left(2x-1\right)\left(x+3\right)}=x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow\sqrt{2x-1}.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow\left(\sqrt{2x-1}-x\right).\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x-1}=x\\\sqrt{2x-1}=2\sqrt{x+3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{13}{2}\left(\text{loại}\right)\end{matrix}\right.\)
Vậy x = 1 là nghiệm phương trình
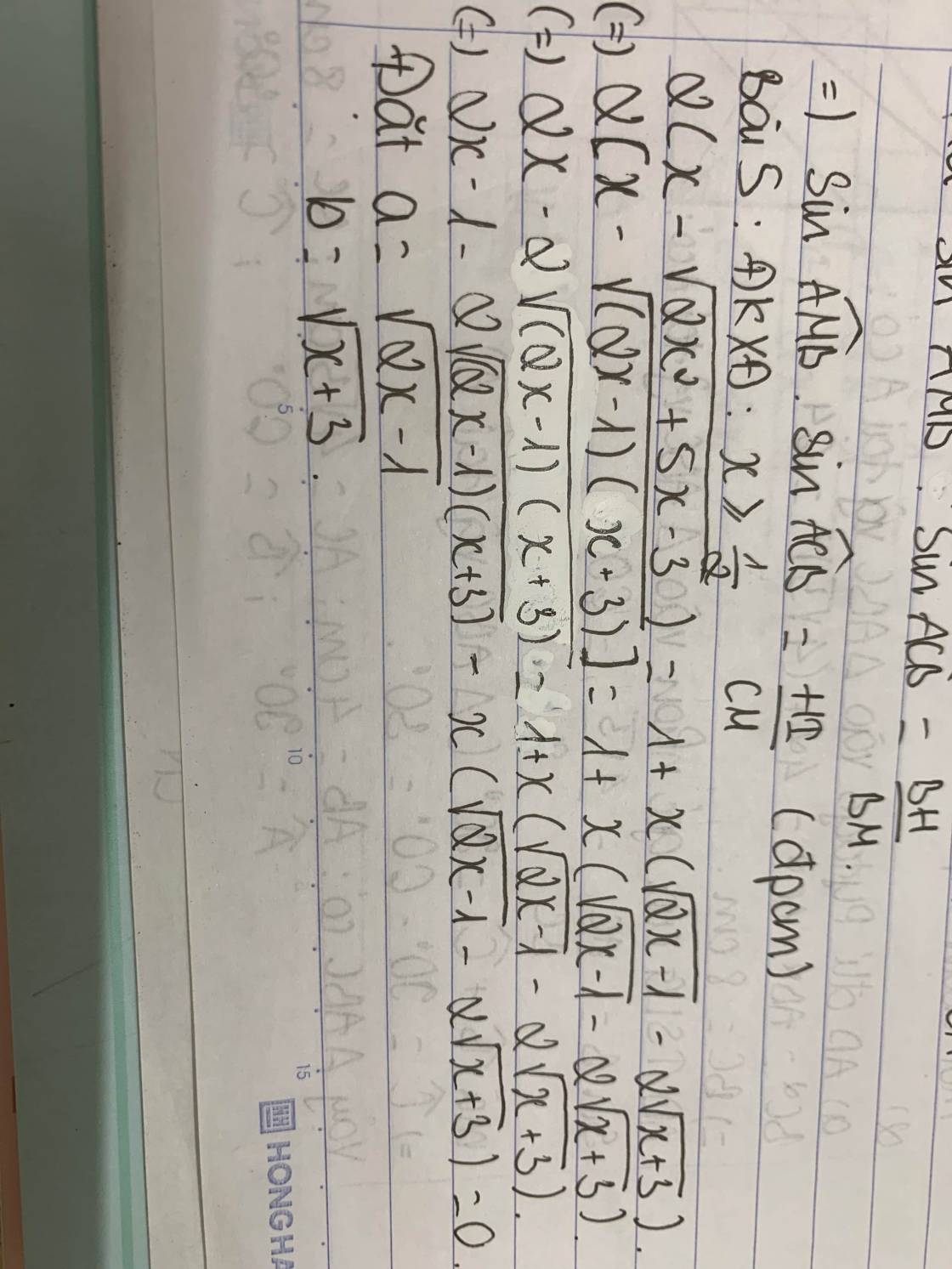
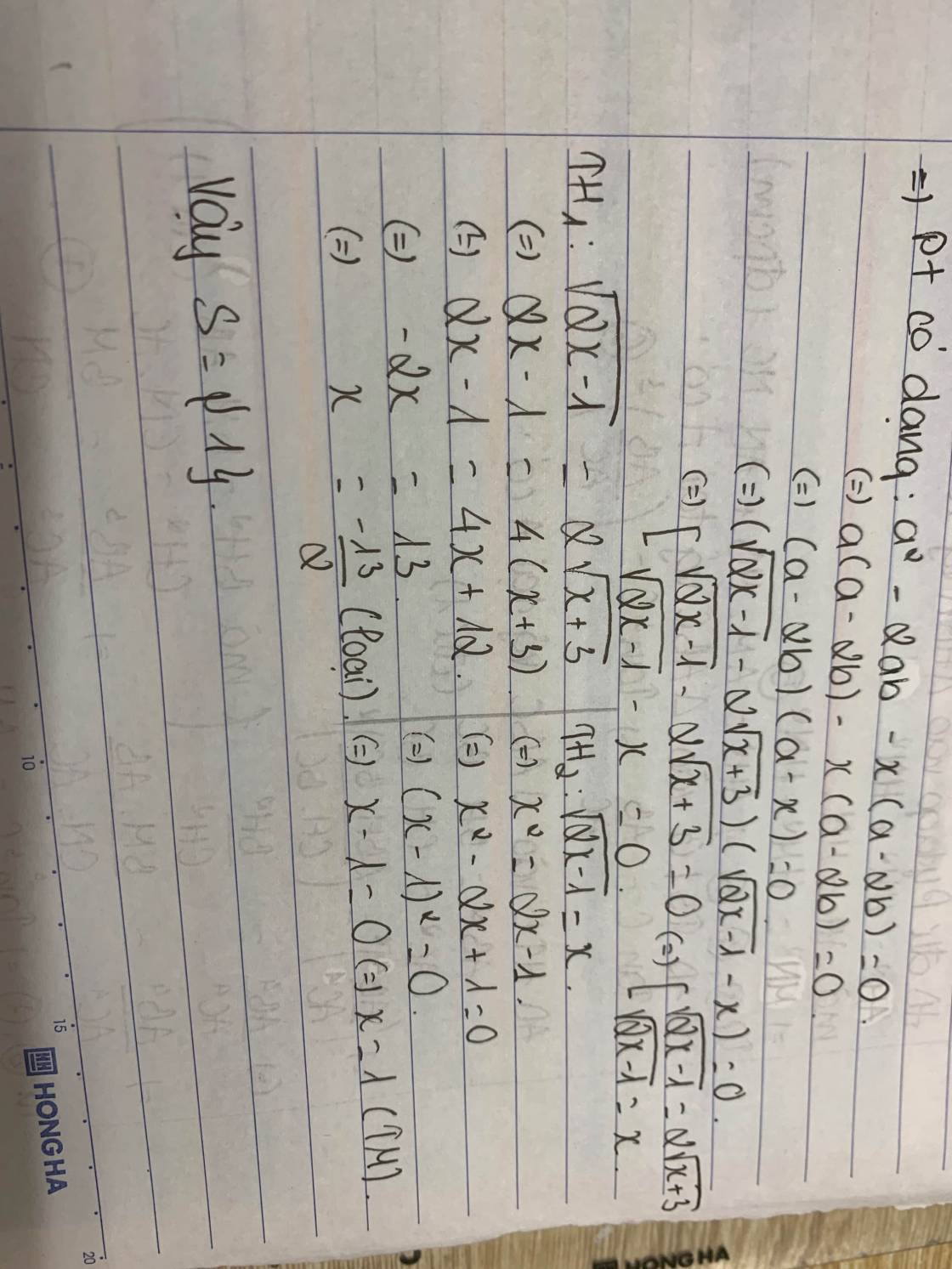






\(x^2+xy+y^2=x^2y^2\)
\(\Leftrightarrow4x^2+4xy+4y^2=4x^2y^2\)
\(\Leftrightarrow4x^2+8xy+4y^2=4x^2y^2-4xy+1-1\)
\(\Leftrightarrow\left(2x+2y\right)^2=\left(2xy-1\right)^2-1\)
\(\Leftrightarrow\left(2xy-1+2x+2y\right)\left(2xy-1-2x-2y\right)=1\)
\(x^2+xy+y^2=x^2y^2\)
\(\Leftrightarrow x^2+2xy+y^2=x^2y^2+xy\)
\(\Leftrightarrow\left(x+y\right)^2=xy\left(xy+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}xy=0\\xy+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\y=0\\xy=-1\end{matrix}\right.\)
(Nếu một số chính phương mà bằng tích của 2 số liên tiếp thì một trong 2 số liên tiếp đó bằng 0)
Nếu \(x=0\) \(\Rightarrow\left(0+y\right)^2=0.y\left(0.y+1\right)\Leftrightarrow y=0\)
Do x và y có vai trò bình đẳng nên khi \(y=0\Rightarrow x=0\)
Nếu \(xy=-1\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\end{matrix}\right.\) (TMĐK)
Vậy pt đã cho có các nghiệm nguyên: \(\left(0;0\right);\left(1;-1\right);\left(-1;1\right)\)