Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$\frac{19}{x+y}+\frac{19}{y+z}+\frac{19}{z+x}=\frac{133}{10}$
$19(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x})=\frac{133}{10}$
$\Rightarrow \frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{133}{10}: 19=\frac{7}{10}(*)$
Lại có:
$\frac{7z}{x+y}+\frac{7x}{y+z}+\frac{7y}{x+z}=\frac{133}{10}$
$\frac{z}{x+y}+\frac{x}{y+z}+\frac{y}{x+z}=\frac{133}{10}:7=\frac{19}{10}$
$\Rightarrow \frac{z}{x+y}+1+\frac{x}{y+z}+1+\frac{y}{x+z}+1=\frac{49}{10}$
$\Rightarrow \frac{x+y+z}{x+y}+\frac{x+y+z}{y+z}+\frac{x+y+z}{x+z}=\frac{49}{10}$
$\Rightarrow (x+y+z)(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{x+z})=\frac{49}{10}$
Sử dụng kq $(*)$ suy ra:
$x+y+z=\frac{49}{10}: \frac{7}{10}=7$


Lời giải:
a.
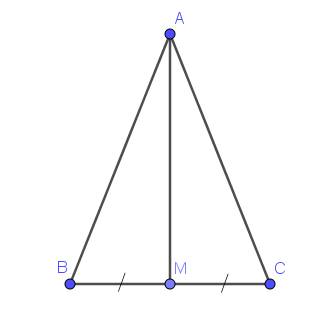
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.

Gọi số bị chia là a, số chia là b, thương là c (a>b>c>0)
Theo bài ra ta có: a:b=c
9a:2b=1098
Từ 9a:2b=1098 suy ra suy ra a:b=1098:9/2=244
Mà a:b=c do đó c=244
Vậy thương của phép chia là 244
Lời giải:
Khi gấp số bị chia lên 9 lần và giảm số chia 2 lần thì thương mới gấp $9\times 2=18$ lần thương cũ.
Thương cũ là:
$1098:18=61$

54,3 x 5,4 + 5,43 : 0,1 x 0,3 + 54,3 x \(\dfrac{43}{10}\)
= 54,3 x 5,4 + 5,43 x 10 x 0,3 + 54,3 x 4,3
= 54,3 x 5,4 + 54,3 x 0,3 + 54,3 x 4,3
= 54,3 x (5,4 + 0,3 + 4,3)
= 54,3 x 10
= 543

124 : x + 24 : x - 48 : x = 25
(124 + 24 - 48) : x = 25
100 : x = 25
x = 100 : 25
x = 4

Để tính phần trăm học sinh con lại so với tổng số học sinh toàn trường, ta sử dụng công thức sau:
Phần trăm = (Số học sinh con lại / Tổng số học sinh toàn trường) x 100%
Trong trường hợp này, số học sinh con lại là 1020 và tổng số học sinh toàn trường là 1700. Áp dụng vào công thức, ta có:
Phần trăm = (1020 / 1700) x 100% = 60%
Vậy, số học sinh con lại chiếm 60% tổng số học sinh toàn trường.
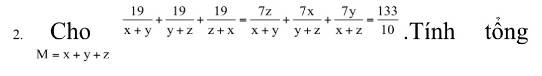
Ta có: \(A=\dfrac{3x-2}{x+2}=\dfrac{3\left(x+2\right)-4}{x+2}=\dfrac{3\left(x+2\right)}{x+2}-\dfrac{4}{x+2}=3-\dfrac{4}{x+2}\)
Để A mang giá trị nguyên khi
\(4⋮x+2\) hay \(x+2\inƯ\left(4\right)\in\left\{\pm1;\pm2;\pm4\right\}\)
Do đó:
\(x+2=-1\Rightarrow x=\left(-1\right)-2\Rightarrow x=-3\)
\(x+2=1\Rightarrow x=1-2\Rightarrow x=-1\)
\(x+2=-2\Rightarrow x=\left(-2\right)-2\Rightarrow x=-4\)
\(x+2=2\Rightarrow x=2-2\Rightarrow x=0\)
\(x+2=-4\Rightarrow x=\left(-4\right)-2\Rightarrow x=-6\)
\(x+2=4\Rightarrow x=4-2\Rightarrow x=2\)
Vậy để A là số nguyên khi \(x\in\left\{-3;-1;-4;0;-6;2\right\}\)