Bác Mai gửi tiết kiệm một số tiền tại một ngân hàng theo thể thức kì hạn 1 năm với lãi suất 5%/năm,tiền lãi sau mỗi năm gửi tiếp kiệm sẽ được nhập vào tiền vốn để tính lãi cho năm tiếp theo. Sau 2 năm gửi bác Mai rút hết tiền về và nhận được cả vốn lẫn lãi là 330 750 000 đồng. Hỏi số tiền ban đầu bác Mai gửi tiết kiệp là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giấcBC nhọn có ba đườngAD BE CF cắt tại H chứng minh Tam giác CDE đồng dạng với tam giác
CAB

Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
\(\widehat{DCA}\) chung
Do đó: ΔCDA~ΔCEB
=>\(\dfrac{CD}{CE}=\dfrac{CA}{CB}\)
=>\(\dfrac{CD}{CA}=\dfrac{CE}{CB}\)
Xét ΔCDE và ΔCAB có
\(\dfrac{CD}{CA}=\dfrac{CE}{CB}\)
\(\widehat{DCE}\) chung
Do đó: ΔCDE~ΔCAB

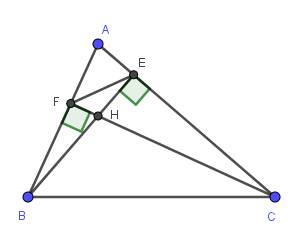
a) Xét hai tam giác vuông: \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (đối đỉnh)
\(\Rightarrow\Delta BHF\) ∽ \(\Delta CHE\) (g-g)
\(\Rightarrow\dfrac{HB}{HC}=\dfrac{HF}{HE}\)
\(\Rightarrow HE.HB=HC.HF\)
b) Xét hai tam giác vuông: \(\Delta AFC\) và \(\Delta AEB\) có:
\(\widehat{A}\) chung
\(\Rightarrow\Delta AFC\) ∽ \(\Delta AEB\) (g-g)
\(\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\)
\(\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
\(\Rightarrow\Delta AEF\) ∽ \(\Delta ABC\) (c-g-c)

Lời giải:
Gọi chiều dài và chiều rộng hcn lớn lần lượt là $a$ cm và $b$ cm
Ta có: $a+b=100:2=50$
Khi chia hcn thành 1 hv và 1 hcn thì ta có 1 hình vuông cạnh $b$ cm và 1 hcn có độ dài 2 chiều là $b$ cm và $a-b$ cm
Chu vi hcn mới: $2(b+a-b)=60$
$\Leftrightarrow a=30$ (cm)
$b=50-a=50-30=20$ (cm)
Vậy độ dài cạnh hcn ban đầu là $20$ cm và $30$ cm

Olm chào em, vấn đề em hỏi Olm xin hỗ trợ như sau:
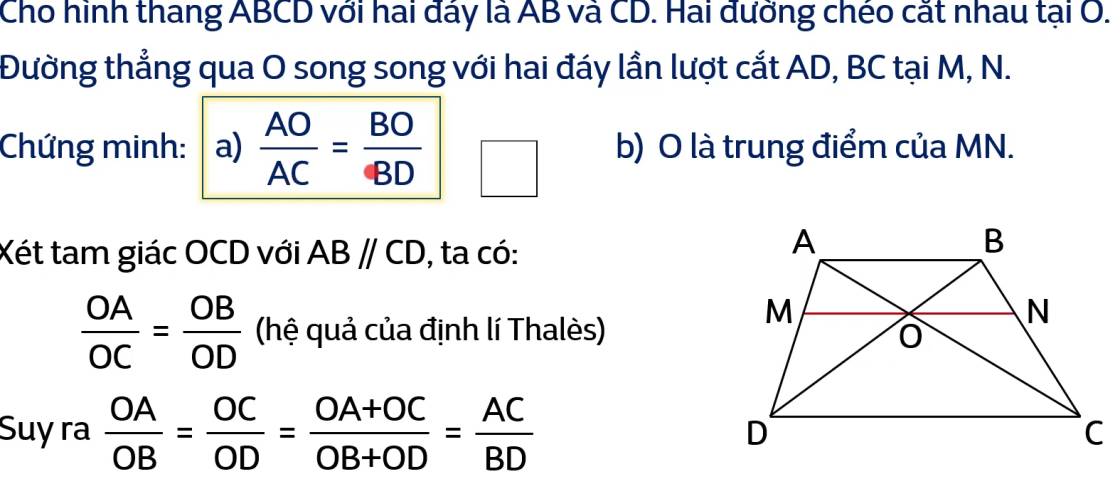
Đoạn \(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả của định lí Thales). Em hiểu rồi đúng chưa.
Từ dòng suy ra \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) = \(\dfrac{AC}{BD}\) là em không hiểu tại sao phải không?
Vậy Olm sẽ giảng cho em như sau:
\(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả định lí Thales) ⇒ \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) (tc tỉ lệ thức)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) (1)
Mặt khác O là giao điểm của AC và BD nên
\(\left\{{}\begin{matrix}OA+OC=AC\\OB+OD=BD\end{matrix}\right.\) (2)
Thay (2) vào (1) ta có: \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{AC}{BD}\)
Giải thích đoạn: \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\)
\(\dfrac{OA}{OB}\) = \(\dfrac{AC}{BD}\) (cmt) ⇒\(\dfrac{AO}{BO}=\dfrac{AC}{BD}\) ⇒ \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\) (tính chất tỉ lệ thức)
Mọi chi tiết bài giảng liên hệ zalo 0385 168 017

\(\dfrac{x+1}{2024}+\dfrac{x+2}{2023}=\dfrac{x+3}{2022}+\dfrac{x+4}{2021}\)
=>\(\left(\dfrac{x+1}{2024}+1\right)+\left(\dfrac{x+2}{2023}+1\right)=\left(\dfrac{x+3}{2022}+1\right)+\left(\dfrac{x+4}{2021}+1\right)\)
=>\(\dfrac{x+2025}{2024}+\dfrac{x+2025}{2023}=\dfrac{x+2025}{2022}+\dfrac{x+2025}{2021}\)
=>\(\left(x+2025\right)\left(\dfrac{1}{2024}+\dfrac{1}{2023}-\dfrac{1}{2022}-\dfrac{1}{2021}\right)=0\)
=>x+2025=0
=>x=-2025

a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔABC~ΔHAC
Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
b: Xét ΔEAB vuông tại A và ΔEFC vuông tại F có
\(\widehat{AEB}=\widehat{FEC}\)(hai góc đối đỉnh)
Do đó: ΔEAB~ΔEFC
=>\(\dfrac{EA}{EF}=\dfrac{EB}{EC}\)
=>\(EA\cdot EC=EB\cdot EF\)

Khoảng cách giữa xe máy và ô tô sau 6 giờ là
45 x 6 = 270 [km]
Hiệu vận tốc là
60 - 45 = 15 [km/giờ]
Thời đi để ô tô đuổi kịp xe máy là
270 : 15 = 18 [giờ]
Đáp số : 18 giờ
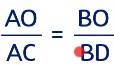
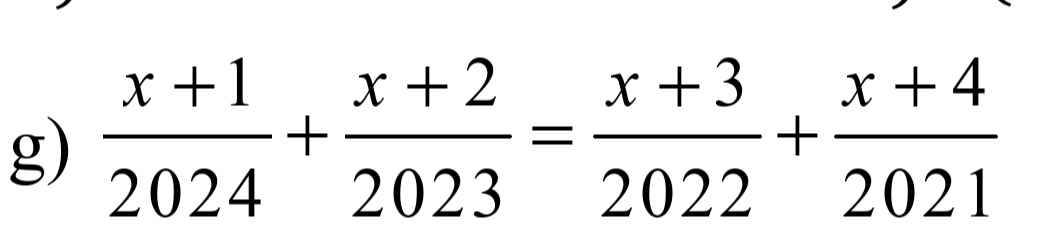
Tỉ số giữa số tiền bác Mai nhận được sau 1 năm so với ban đầu là:
100%+5%=105%
Tỉ số giữa số tiền bác Mai nhận được sau 2 năm so với số tiền gốc là:
105%*105%=1,1025
Số tiền gốc bác Mai gửi tiết kiệm là:
\(\dfrac{330750000}{1,1025}=300000000\left(đồng\right)\)
Gọi số tiền bác gửi ban đầu là x đồng (với x>0)
Số tiền cả vốn lẫn lãi sau 1 năm là:
\(x+5\%.x=1,05x\) (đồng)
Số tiền cả gốc lẫn lãi sau 2 năm là:
\(1,05x+1,05x.5\%=1,1025x\) (đồng)
Do sau 2 năm bác rút được 330 750 000 đồng nên ta có pt:
\(1,1025x=330\text{ }750\text{ }000\)
\(\Rightarrow x=300\text{ }000\text{ }000\) (đồng)