Bài 2. (1,5 điểm) Một ca nô đi xuôi khúc sông từ $A$ đến $B$ hết $1$ giờ $30$ phút và đi ngược từ $B$ về $A$ hết $2$ giờ. Biết vận tốc dòng nước là $3$ km/h. Tính vận tốc riêng của ca nô và chiều dài quãng sông $AB$?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 3x - 4 = 5 + x
3x - 2x = 5 + 4
x = 9
Vậy S = {9}
b) 3(x - 1) - 7 = 5(x + 2)
3x - 3 - 7 = 5x + 10
3x - 10 = 5x + 10
3x - 5x = 10 + 10
-2x = 20
x = 20 : (-2)
x = -10
Vậy S = {-10}

(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c
a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab
ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab
(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab
(a + b + c)x = (a + b + c)²
x = (a + b + c)²/(a + b + c)
x = a + b + c
Vậy S = {a + b + c}
Ta có:
Điều kiện xác định:
Khi đó:
+ Nếu thì phương trình có vô số nghiệm.
+ Nếu thì phương trình có nghiệm duy nhất .

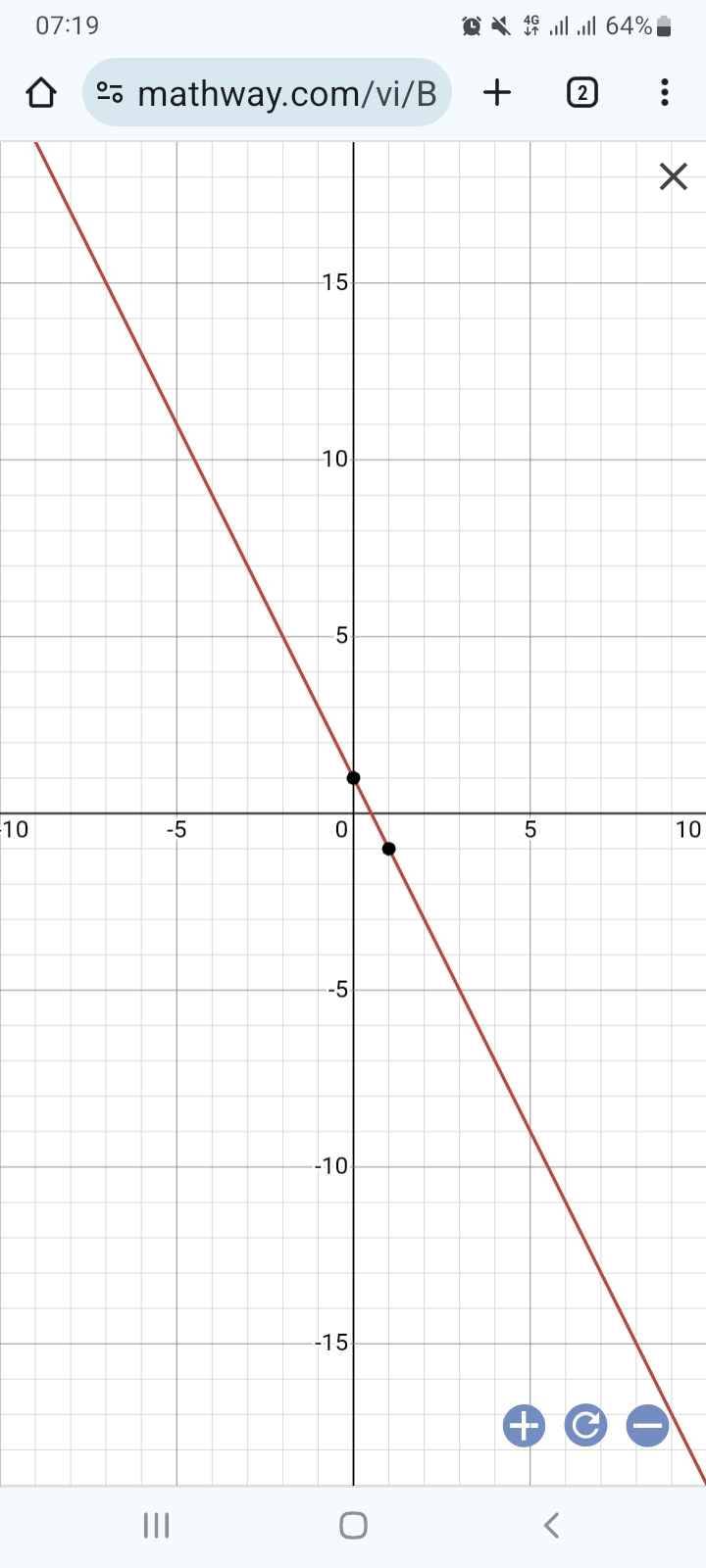
a) Với , hàm số trở thành .
Xét hàm số :
Thay thì .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Thay thì .
Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Vẽ đồ thị:
Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)
20 phút = 1/3 h
Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)
Quãng đường đi từ thành phố về quê: 30x (km)
Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)
Theo đề bài, ta có phương trình:
30x = 25(x + 1/3)
30x = 25x + 25/3
30x - 25x = 25/3
5x = 25/3
x = 25/3 : 5
x = 5/3 (nhận)
Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a) 3x - 5 = 4
3x = 4 + 5
3x = 9
x = 9 : 3
x = 3
Vậy S = {3}
b) 2x/3 + (3x - 1)/6 = x/2
4x + 3x - 1 = 3x
7x - 3x = 1
4x = 1
x = 1/4
Vậy S = {1/4}

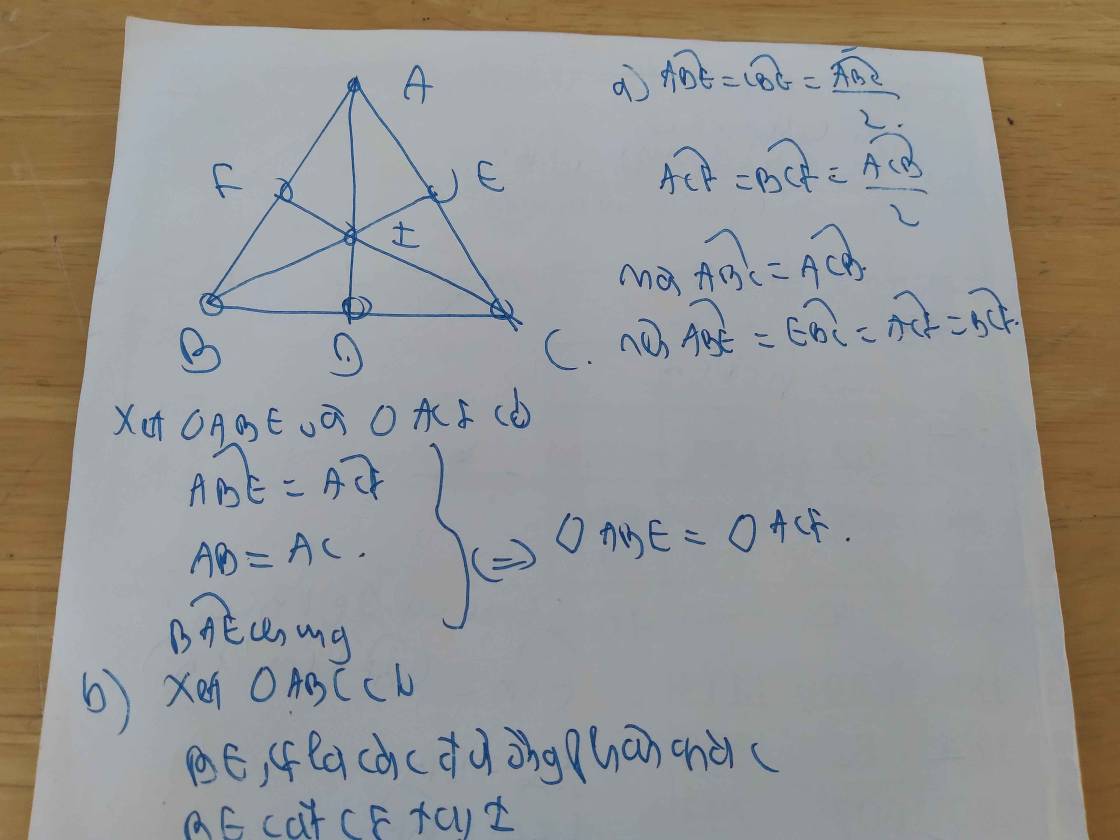
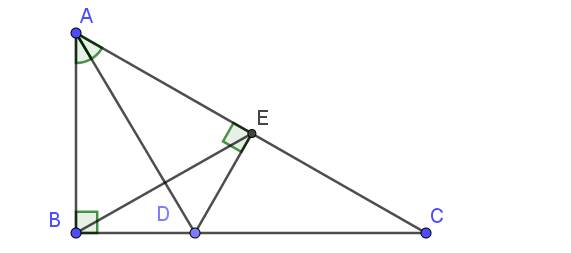
Lời giải:
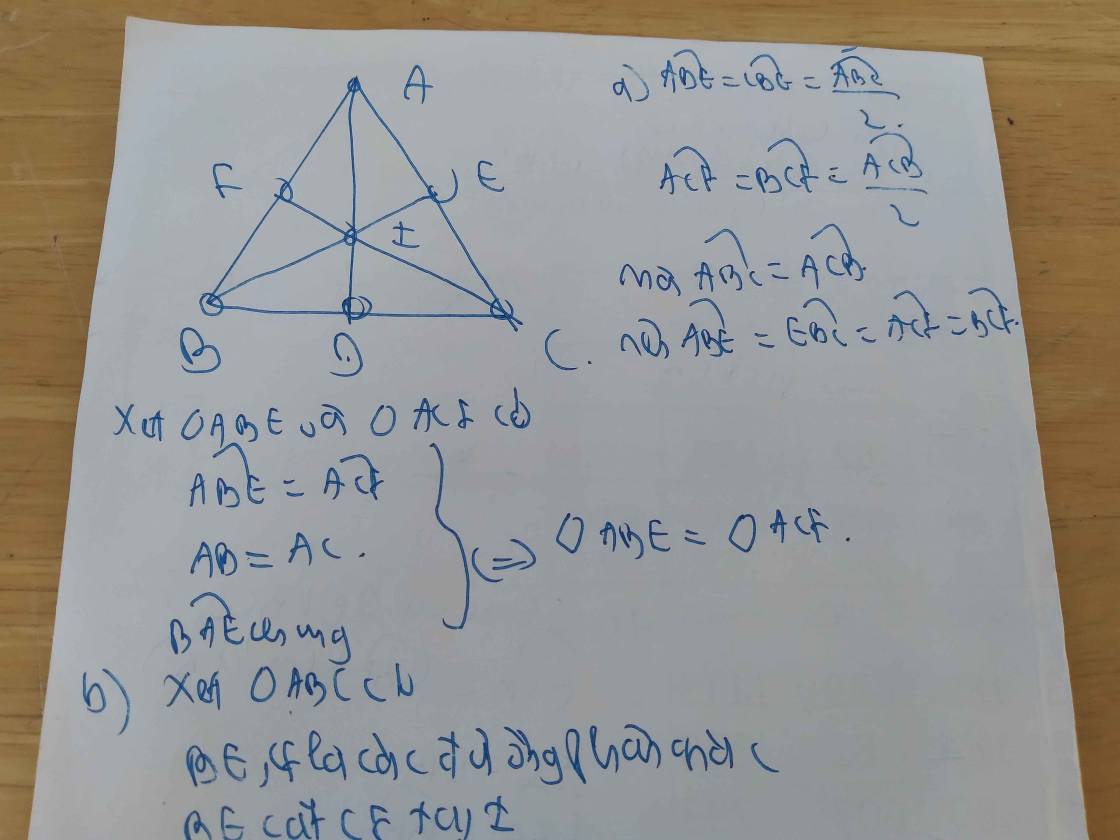
a.
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
b.
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.








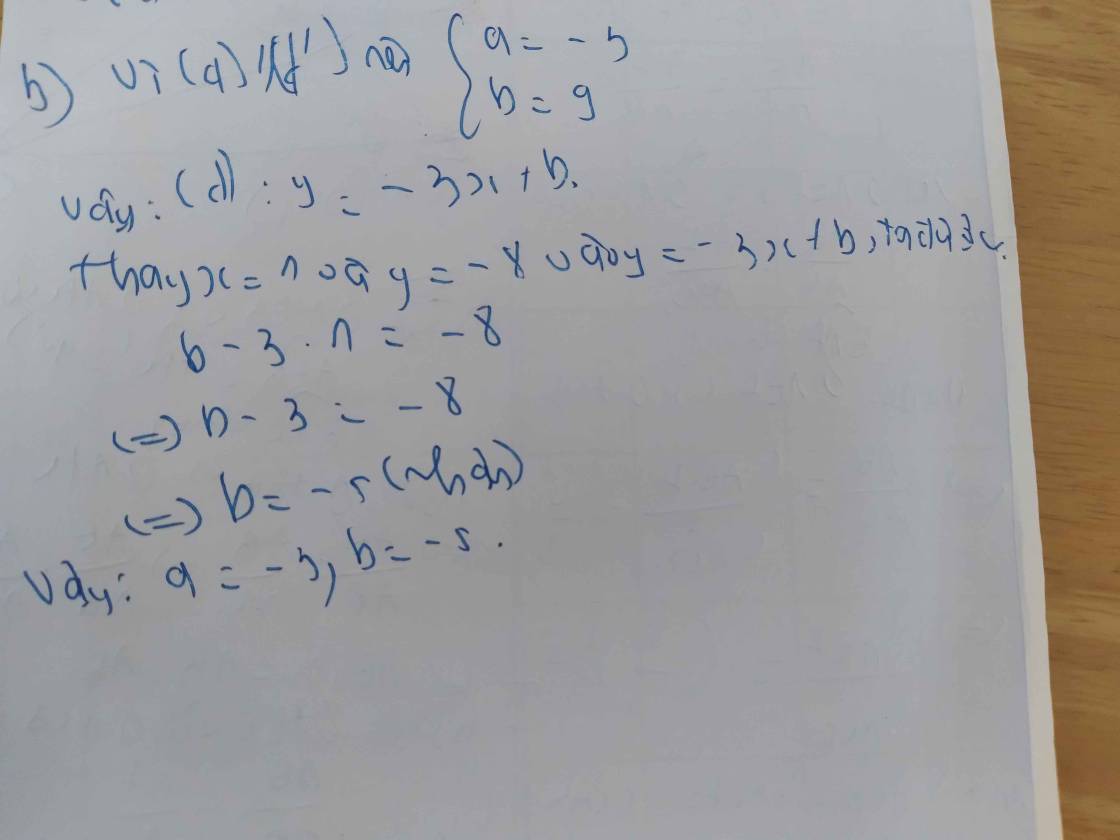

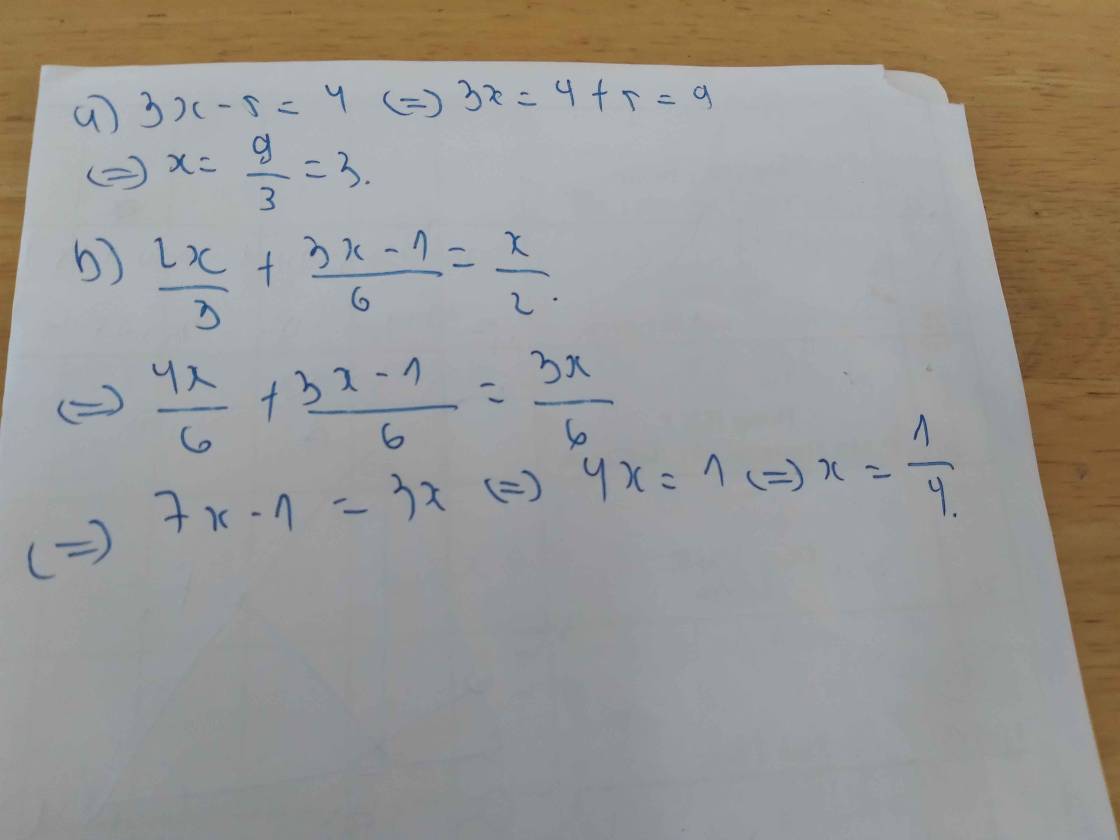





Giải:
Đổi 1 giờ 30 phút = 1,5 giờ
Cứ một giờ ca nô xuôi dòng được: 1 : 1,5 = \(\dfrac{2}{3}\)(quãng sông AB)
Cứ một giờ ca nô ngược dòng được: 1 : 2 = \(\dfrac{1}{2}\) (quãng sông AB)
Cứ một giờ dòng nước chảy được: (\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) : 2 = \(\dfrac{1}{12}\)(quãng sông AB)
Quãng sông AB dài là: 3 : \(\dfrac{1}{12}\) = 36 (km)
Vận tốc ca nô khi ngược dòng là: 36 : 2 = 18 (km/h)
Vận tốc riêng của ca nô là: 18 + 3 = 21 (km/h)
Kết luận: Quãng sông AB dài 36 km
Vận tốc riêng của ca nô là 21 km/h
Gọi x (km/h) là vận tốc riêng của ca nô (x > 3)
Vận tốc đi xuôi dòng từ A đến B: x + 3 (km/h)
1 giờ 30 phút = 1,5 giờ
Quãng đường đi xuôi dòng: (x + 3).1,5 (km)
Vận tốc đi ngược dòng từ B về A: x - 3 (km/h)
Quãng đường đi ngược dòng: (x - 3).2 (km)
Do đi cùng một quãng đường AB nên ta có phương trình:
(x + 3).1,5 = (x - 3).2
1,5x + 4,5 = 2x - 6
2x - 1,5x = 4,5 + 6
0,5x = 10,5
x = 10,5 : 0,5
x = 21 (nhận)
Vậy vận tốc riêng của ca nô là 21 km/h