VD5. Đặt a = x - y , b = y - z , c = z - x

=> a + b + c = 0

nên P = (x  - y)³ + (y - z)³ + (z - x)³ 

= a³ + b³ + c³ 

= (a + b)³ - 3ab(a + b) + c³ 

= (-c)³ - 3ab(-c) + c³ 

= 3abc = 3(x - y)(y - z)(z - x)

VD7 : Đặt x + y - z = a ; x - y + z = b ; -x + y + z = c

ta thấy : a + b + c = x + y + z 

Nên ta được Q = (x + y + z)³ - (x + y - z)³ - (x - y + z)³ - (-x + y + z)³

= (a + b + c)³ - a³ - b³ - c³ 

= (a + b)³ + 3(a + b)²c + 3(a + b)c² + c³ - a³ - b³ - c³

= a³ + b³ + 3ab(a + b) + 3(a + b)c(a + b + c) + c³ - a³ - b³ - c³ 

= 3(a + b)[ab + c.(a + b + c)] 

 = 3(a + b)(b + c)(c + a)

= 24xyz

a) \(\left(x+2y\right)^2-\left(x-y\right)^2=\left(x+2y+x-y\right)\left(x+2y-x+y\right)\)

\(=\left(2x+y\right).3y\)

b) \(\left(x+1\right)^3+\left(x-1\right)^3\)

\(=\left(x+1+x-1\right)\left[\left(x+1\right)^2-\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\right]\)

\(=2x\left[\left(x+1\right)^2-\left(x^2-1\right)+\left(x-1\right)^2\right]\)

c) \(9x^2-3x+2y-4y^2\)

\(=9x^2-4y^2-3x+2y\)

\(=\left(3x-2y\right)\left(3x+2y\right)-\left(3x-2y\right)\)

\(=\left(3x-2y\right)\left[3x+2y-1\right]\)

d) \(4x^2-4xy+2x-y+y^2\)

\(=4x^2-4xy+y^2+2x-y\)

\(=\left(2x-y\right)^2+2x-y\)

\(=\left(2x-y\right)\left(2x-y+1\right)\)

e) \(x^3+3x^2+3x+1-y^3\)

\(=\left(x+1\right)^3-y^3\)

\(=\left(x+1-y\right)\left[\left(x+1\right)^2+y\left(x+1\right)+y^2\right]\)

g) \(x^3-2x^2y+xy^2-4x\)

\(=x\left(x^2-2xy+y^2\right)-4x\)

\(=x\left(x-y\right)^2-4x\)

\(=x\left[\left(x-y\right)^2-4\right]\)

\(=x\left(x-y+2\right)\left(x-y-2\right)\)

a) (x + 2y)² - (x - y)²

= (x + 2y - x + y)(x + 2y + x - y)

= 3y(2x + y)

b) (x + 1)³ + (x - 1)³

= (x + 1 + x - 1)[(x + 1)² - (x + 1)(x - 1) + (x - 1)²]

= 2x(x² + 2x + 1 - x² + 1 + x² - 2x + 1)

= 2x(x² + 3)

c) 9x² - 3x + 2y - 4y²

= (9x² - 4y²) - (3x - 2y)

= (3x - 2y)(3x + 2y) - (3x - 2y)

= (3x - 2y)(3x + 2y - 1)

d) 4x² - 4xy + 2x - y + y²

= (4x² - 4xy + y²) + (2x - y)

= (2x - y)² + (2x - y)

= (2x - y)(2x - y + 1)

e) x³ + 3x² + 3x + 1 - y³

= (x³ + 3x² + 3x + 1) - y³

= (x + 1)³ - y³

= (x + 1 - y)[(x + 1)² + (x + 1)y + y²]

= (x - y + 1)(x² + 2x + 1 + xy + y + y²)

g) x³ - 2x²y + xy² - 4x

= x(x² - 2xy + y² - 4)

= x[(x² - 2xy + y²) - 4]

= x[(x - y)² - 2²]

= x(x - y - 2)(x - y + 2)

2.26:

a. $x^2-6x+9-y^2=(x^2-6x+9)-y^2=(x-3)^2-y^2$
$=(x-3-y)(x-3+y)$

b. $4x^2-y^2+4y-4=4x^2-(y^2-4y+4)$

$=(2x)^2-(y-2)^2=(2x-y+2)(2x+y-2)$
c. $xy+z^2+xz+yz=(xy+xz)+(z^2+yz)=x(y+z)+z(z+y)$
$=(y+z)(x+z)$
c.

$x^2-4xy+4y^2+xz-2yz$
$=(x^2-4xy+4y^2)+(xz-2yz)$
$=(x-2y)^2+z(x-2y)=(x-2y)(x-2y+z)$

2.27:

a. $x^3+y^3+x+y=(x^3+y^3)+(x+y)$
$=(x+y)(x^2-xy+y^2)+(x+y)=(x+y(x^2-xy+y^2+1)$
b. $x^3-y^3+x-y=(x^3-y^3)+(x-y)=(x-y)(x^2+xy+y^2)+(x-y)$

$=(x-y)(x^2+xy+y^2+1)$

c.

$(x-y)^3+(x+y)^3=(x^3-3x^2y+3xy^2-y^3)+(x^3+3x^2y+3xy^2+y^3)$
$=2x^3+6xy^2=2x(x^2+3y^2)$

d.

$x^3-3x^2y+3xy^2-y^3+y^2-x^2$
$=(x^3-3x^2y+3xy^2-y^3)-(x^2-y^2)$
$=(x-y)^3-(x-y)(x+y)=(x-y)[(x-y)^2-(x+y)]$

$=(x-y)(x^2-2xy+y^2-x-y)$

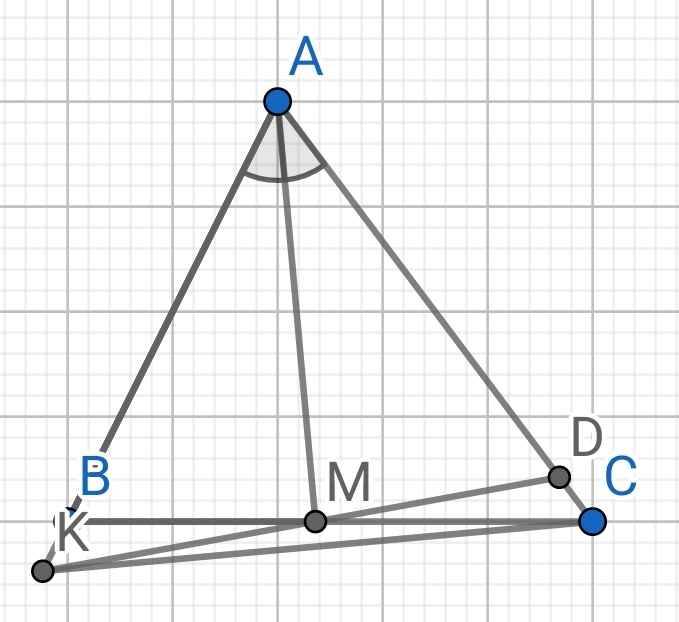 a) Do AM là tia phân giác của ∆BAC (gt)

⇒ ∠BAM = ∠DAM

Xét ∆ABM và ∆ADM có:

AB = AD (gt)

∠BAM = ∠DAM (cmt)

AM là cạnh chung

⇒ ∆ABM = ∆ADM (c-g-c)

⇒ BM = MD (hai cạnh tương ứng)

b) Do ∆ABM = ∆ADM (cmt)

⇒ ∠ABM = ∠ADM (hai góc tương ứng)

⇒ ∠ABC = ∠ADK

Xét ∆DAK và ∆BAC có:

∠ADK = ∠ABC (cmt)

AD = AB (gt)

∠A chung

⇒ ∆DAK = ∆BAC (g-c-g)

c) Do ∆DAK = ∆BAC (cmt)

⇒ AK = AC (hai cạnh tương ứng)

∆AKC có AK = AC (cmt)

⇒ ∆AKC cân tại A

a) \(\dfrac{a}{b}=\dfrac{c}{d}\left(a;b;c;d\ne0\right)\)

 \(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)

\(\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)

\(\Rightarrow dpcm\)

b) \(\dfrac{a}{b}=\dfrac{c}{d}\)

\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)

\(\Rightarrow\dfrac{5a}{5c}=\dfrac{3b}{3d}=\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)

\(\Rightarrow\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\)

\(\Rightarrow dpcm\)

Thanks

a) \(\dfrac{1}{4}x^2y^3\cdot\left(-\dfrac{2}{3}xy\right)\)

\(=\left(\dfrac{1}{4}\cdot-\dfrac{2}{3}\right)\cdot\left(x^2\cdot x\right)\cdot\left(y^3\cdot y\right)\)

\(=-\dfrac{1}{6}x^3y^4\)

b) \(\left(2x^3\right)^3\cdot\left(-5xy^2\right)\)

\(=8x^9\cdot\left(-5xy^2\right)\)

\(=\left(8\cdot-5\right)\cdot\left(x^9\cdot x\right)\cdot y^2\)

\(=-40x^{10}y^2\)

a) \(\dfrac{1}{4}x^2y^3.\left(-\dfrac{2}{3}xy\right)\)

\(=-\dfrac{1}{6}x^3y^4\)

Nên bậc của đơn thức là 7

b) \(\left(2x^3\right)^3.\left(-5xy^2\right)\)

\(=8x^9.\left(-5xy^2\right)\)

\(=-40x^9y^2\)

Nên bậc của đơn thức là 11

a) Ta có:

\(4x^2-6x=\left(2x.2x-3\right)\)

b) Ta có:

\(9x^4y^3+3x^2y^4\)

\(=3x^2y^3\left(3x^2+y\right)\)

c) Ta có:

\(x^3-2x^2+5x\)

\(=x\left(x^2-2x+5\right)\)

a) \(4x^2-6x=2x\left(2x-3\right)\)

b) \(9x^4y^3+3x^2y^4=3x^2y^3\left(3x^2+y\right)\)

c) \(3\left(x-y\right)-5x\left(y-x\right)=3\left(x-y\right)+5x\left(x-y\right)=\left(x-y\right)\left(3+5x\right)\)

d) \(5x\left(x-3y\right)-15x\left(3y-x\right)\)

\(=5x\left(x-3y\right)+15x\left(x-3y\right)\)

\(=\left(x-3y\right)\left(5x+15x\right)\)

\(=16x\left(x-3y\right)\)

A B C M H N I E Q K D

a/

\(BN\perp AC;MH\perp AC\) => MH//BN

Xét tg BNC có

MH//BN

MB=MC

=> HN=HC (trong tg đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)

Ta có

MH//BN. Xét tg AMH

\(\dfrac{ED}{IM}=\dfrac{EN}{IH}\) (talet)

Mà IM=IH => ED=EN

b/

Xét tg vuông ABN có

\(BN^2=AB^2-AN^2=AC^2-AN^2=\)

\(=AC^2-\left(AC-CN\right)^2=AC^2-\left(AC-2HN\right)^2=\)

\(=AC^2-AC^2+4AC.HN-4HN^2=\)

\(=4HN.\left(AC-HN\right)=4HN\left(AC-HC\right)=\)

\(=4HN.HA\)

Xét tg BCN có

MB=MC; HN=HC => MH là đường trung bình => \(MH=\dfrac{BN}{2}\)

Mà MH=2MI\(\Rightarrow2MI=\dfrac{BN}{2}\Rightarrow BN=4MI\)

Ta có

\(BN^2=4HN.HA\Rightarrow\left(4MI\right)^2=4HN.HA\)

\(\Rightarrow16MI^2=4.HN.HA\Rightarrow MI^2=HN.HA\)

Ta có : \(B\text{=}4x^2-12x+9\)

\(B\text{=}\left(2x-3\right)^2\)

Với \(x\text{=}\dfrac{1}{2}\)

\(\Rightarrow B\text{=}\left(2.\dfrac{1}{2}-3\right)^2\)

\(B\text{=}\left(-2\right)^2\text{=}4\)

Ta có : \(A\text{=}5\left(x+3\right)\left(x-3\right)+\left(2x+3\right)^2+\left(x-6\right)^2\)

\(A\text{=}5\left(x^2-9\right)+\left(2x+3\right)^2+\left(x-6\right)^2\)

\(A\text{=}5x^2-45+4x^2+12x+9+x^2-12x+36\)

\(A\text{=}10x^2\)

Với \(x\text{=}-\dfrac{1}{5}\)

\(\Rightarrow A\text{=}10.\left(-\dfrac{1}{5}\right)^2\text{=}\dfrac{2}{5}\)

B = 4x² - 12x + 9

= (2x - 3)²

Tại x = 1/2 ta có:

B = (2.1/2 - 3)²

= (-2)²

= 4

-------------------

A = 5(x + 3)(x - 3) + (2x + 3)² + (x - 6)²

= 5x² - 45 + 4x² + 12x + 9 + x² - 12x + 36

= 10x²

Tại x = 1/5 ta có:

A = 10.(1/5)²

= 2/5