Ta có: \(xy-2x+3y=-5\)

\(\Rightarrow\left(xy-2x\right)+3y-6=-5-6\)

\(\Rightarrow x\left(y-2\right)+3\left(y-2\right)=-11\)

\(\Rightarrow\left(x+3\right)\left(y-2\right)=-11\)

Vì \(x,y\) nguyên nên \(x+3;y-2\) có giá trị nguyên

\(\Rightarrow x+3;y-2\) là các ước của \(-11\)

Ta có bảng sau:

Vì \(x,y\) nguyên nên ta được các cặp giá trị \(\left(x;y\right)\) là:

\(\left(-2;-9\right);\left(8;1\right);\left(-4;13\right);\left(14;3\right)\)

\(Toru\)

trả lời được tao cho thêm tiền

39.85133474812912

2\(\sqrt{3}\) - \(\sqrt{4+x^2}\) = 0    vì 4 + \(x^2\) ≥ 0 ∀ \(x\) vậy \(\sqrt{4+x^2}\) có nghĩa với ∀\(x\)

2\(\sqrt{3}\) - \(\sqrt{4+x^2}\) = 0

          \(\sqrt{4+x^2}\)  = 2\(\sqrt{3}\)

           4 + \(x^2\)   = 12

                \(x^2\)      = 12 - 4

                \(x^2\)      = 8

               \(\left[{}\begin{matrix}x=-\sqrt{8}\\x=\sqrt{8}\end{matrix}\right.\)

               \(\left[{}\begin{matrix}x=-2\sqrt{2}\\x=2\sqrt{2}\end{matrix}\right.\)

                \(\left[{}\begin{matrix}x=-2\sqrt{2}\\x=2\sqrt{2}\end{matrix}\right.\)

(-8).82+(-8).38+8.20

= (-8).82+(-8).38+(-8).(-20)

= (-8).(82+38-20)

= (-8).100 = -800

Chữ không có tâm đối xứng là của S.

Chọn C.

chu nao do nha moi nguoi

Ta có:\(81=9.9\)

\(\Rightarrow\)Cạnh hình vuông là \(9dm\)

Chu vi hình vuông là:

 \(9.4=36\left(dm\right)\)

Vì chu vi hình vuông bằng \(36dm\) nên chu vi hình chữ nhật bằng \(36dm\)

Chiều dài hình chữ nhật là:

 \(36:2-4=14\left(dm\right)\)

Diện tích hình chữ nhật là:

\(14.4=56\left(dm^2\right)\)

   Đ/S:...

Lời giải:

Vì $81=9\times 9$ nên độ dài cạnh hình vuông là $9$ dm 

Chu vi hình chữ nhật là: $9\times 4=36$ (dm) 

Nửa chu vi hình chữ nhật: $36:2=18$ (dm)

Chiều dài hình chữ nhật: $18-4=14$ (dm)

Diện tích hình chữ nhật: $14\times 4=56$ (dm²)

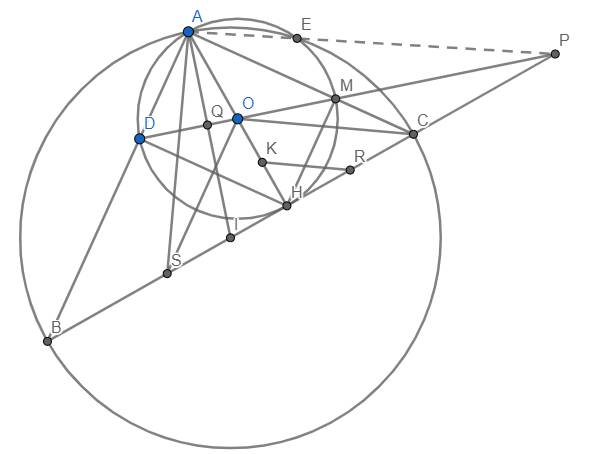
a) Chứng minh tam giác ABH vuông tại H và \(DH\perp AB\) rồi dùng hệ thức lượng \(\Rightarrow AD.AB=AH^2\). Tương tự, ta có \(AM.AC=AH^2\). Do đó \(AD.AB=AM.AC\) và theo bổ đề quen thuộc thì tứ giác BCMD nội tiếp. (đpcm)

b) Gọi Q là giao điểm của DM và AI. Khi đó tam giác ABC vuông tại A có trung tuyến AI nên \(IA=IB=IC=\dfrac{BC}{2}\) hay tam giác IBA cân tại I, suy ra \(\widehat{B}=\widehat{DAQ}\).

 Lại có \(\widehat{B}+\widehat{ACB}=90^o\) suy ra \(\widehat{DAQ}+\widehat{ADQ}=90^o\) (do \(\widehat{ADQ}=\widehat{ACB}\) (cmt)). Do đó \(PQ\perp AI\) tại Q. Từ đó dễ dàng chứng minh O là trực tâm tam giác AIP.

 c) Do tứ giác BCMD nội tiếp nên \(PM.PD=PC.PB\) \(\Rightarrow P_{P/\left(O\right)}=P_{P/\left(I\right)}\) \(\Rightarrow\) P nằm trên trục đẳng phương của (O) và (I). Lại có AE chính là trục đẳng phương của (O) và (I) nên A, E, P thẳng hàng. (đpcm)

 d) Ta thấy SO//AB \(\perp AC\) và \(AH\perp BC\) nên O là trực tâm tam giác ASC \(\Rightarrow OC\perp AS\)

 Lại có OC//KR nên \(RK\perp SA\) (đpcm)

 Ở bài này chứng minh được \(A\in\left(I\right)\) vì BC là đường kính của (I) và \(\widehat{BAC}=90^o\)

2,5 x 6 + 3 x 2,5 + 2,5

= 2,5 x 6 + 3 x 2,5 + 2,5 x 1

= 2,5 x ( 6 + 3 + 1 )

= 2,5 x        10

=              25

cho mih 1 tick nha

   -36 - 12

= -(36 + 12)

= - 48

Chọn D. - 48 

 -36 - 12

= -(36 + 12)

= - 48