7\(x\).2 hay 7\(x^2\) vậy em?

7x^2 ạ

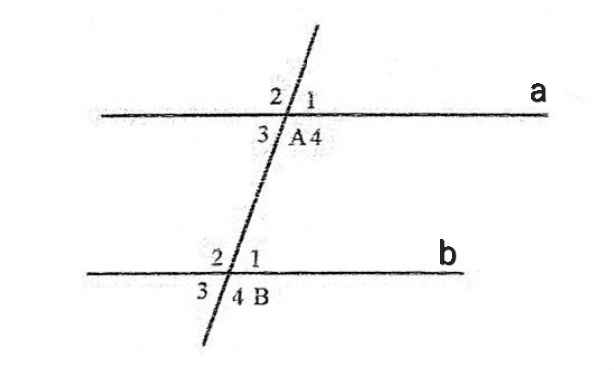
Ta có:

∠A₃ = ∠B₁ (gt)

Mà ∠A₃ và ∠B₁ là hai góc so le trong

⇒ a // b

⇒ ∠A₂ = ∠B₂ (đồng vị)

Do ∠A₃ + ∠A₄ = 180⁰ (kề bù)

Mà ∠A₃ = ∠B₁ (gt)

⇒ ∠B₁ + ∠A₄ = 180⁰

\(M=\dfrac{202}{7\cdot1010}+\dfrac{202}{10\cdot1313}+\dfrac{202}{13\cdot1616}+...+\dfrac{202}{91\cdot9494}\\ =\dfrac{202}{7\cdot10\cdot101}+\dfrac{202}{10\cdot13\cdot101}+\dfrac{202}{13\cdot16\cdot101}+...+\dfrac{202}{91\cdot94\cdot101}\\ =\dfrac{202}{101}\cdot\left(\dfrac{1}{7\cdot10}+\dfrac{1}{10\cdot13}+\dfrac{1}{13\cdot16}+...+\dfrac{1}{91\cdot94}\right)\\ =\dfrac{2}{3}\cdot\left(\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+...+\dfrac{3}{91\cdot94}\right)\\ =\dfrac{2}{3}\cdot\left(\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{91}-\dfrac{1}{94}\right)\\ =\dfrac{2}{3}\cdot\left(\dfrac{1}{7}-\dfrac{1}{94}\right)\\ =\dfrac{2}{3}\cdot\dfrac{87}{658}\\ =\dfrac{29}{329}\)

Ta có:

\(\left|x-\dfrac{1}{3}\right|+\left|x-\dfrac{1}{15}\right|+...+\left|x-\dfrac{1}{399}\right|\ge0\forall x\)

\(\Rightarrow-11x\ge0\forall x\Rightarrow x\le0\)

\(\Rightarrow x-\dfrac{1}{3};x-\dfrac{1}{15};...;x-\dfrac{1}{399}< 0\)

\(\Rightarrow x-\dfrac{1}{3}+x-\dfrac{1}{15}+...+x-\dfrac{1}{399}=11x\)

\(\Rightarrow x+x+...+x-\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{19.21}\right)=11x\)

Vì số lượng \(x\) ở vế trái bằng số lượng số hạng là phân số

\(\Rightarrow\) Số lượng \(x\) ở vế trái là:\(\left(19-1\right):2+1=10\left(số\right)\)

\(\Rightarrow10x-\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)=11x\)

\(\Rightarrow-x=1-\dfrac{1}{21}\)

\(\Rightarrow x=-\dfrac{20}{21}\)

\(a.\dfrac{-3}{7}\cdot\dfrac{15}{13}-\dfrac{3}{7}\cdot\dfrac{11}{13}-\dfrac{3}{7}\\ =-\dfrac{3}{7}\cdot\left(\dfrac{15}{13}+\dfrac{11}{13}+1\right)\\ =-\dfrac{3}{7}\cdot\left(\dfrac{26}{13}+1\right)\\ =\dfrac{-3}{7}\cdot3\\ =\dfrac{-9}{7}\\ b.\dfrac{-1}{9}\cdot\dfrac{-3}{5}+\dfrac{5}{-6}\cdot\dfrac{-3}{5}-\dfrac{7}{2}\cdot\dfrac{3}{5}\\ =-\dfrac{3}{5}\cdot\left(\dfrac{-1}{9}+\dfrac{-5}{6}+\dfrac{7}{2}\right)\\ =-\dfrac{3}{5}\cdot\dfrac{23}{9}\\ =-\dfrac{23}{15}\)

\(Ư\left(240\right)=\left\{\text{1;2,3,4,5,6,8,10,24,30,40,48,60,80,120,240}\right\}\)

240 = 2⁴.3.5 

Ư(240) ={1;2;3;4;5;6;8;10;12;15;16;20;24;30;40;48;60;80;120;240}

\(\overline{ab}+\overline{cd}+\overline{eg}⋮9\)

\(\overline{ab}+\overline{cd}+\overline{eg}=10a+b+10c+d+10e+g=\)

\(=9\left(a+c+e\right)+\left(a+b+c+d+e+g\right)⋮9\)

Ta có \(9\left(a+c+e\right)⋮9\)

\(\Rightarrow a+b+c+d+e+g⋮9\)

\(\Rightarrow\overline{abcdeg}⋮9\)

\(\dfrac{2}{1\cdot6}+\dfrac{2}{11\cdot16}+...+\dfrac{2}{x\left(x+5\right)}=\dfrac{41}{103}\\ =>\dfrac{2}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{x\left(x+5\right)}\right)=\dfrac{41}{103}\\ =>1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{x}-\dfrac{1}{x+5}=\dfrac{41}{103}:\dfrac{2}{5}=\dfrac{205}{206}\\ =>1-\dfrac{1}{x+5}=\dfrac{205}{206}\\ =>1-\dfrac{1}{x+5}=1-\dfrac{1}{206}\\ =>\dfrac{1}{x+5}=\dfrac{1}{206}\\ =>x+5=206\\ =>x=206-5=201\)

\(3^{x+1}=27\)

\(3^{x+1}=3^3\)

\(\Rightarrow x+1=3\)

\(x=3-1\)

\(x=2\)

Vậy x = 2.

\(#Paciupibijd\)

\(3^{x+1}=27\)

\(\Rightarrow3^{x+1}=3^3\)

\(\Rightarrow x+1=3\)

\(\Rightarrow x=3-1\)

\(\Rightarrow x=2\)

TH1: `2<=x<=3` 

\(\left(2x-4\right)+\left(3-x\right)=2x\\ =>2x-4+3-x=2x\\ =>x-1=2x\\ =>2x-x=-1\\ =>x=-1\left(ktm\right)\)

TH2: `x>3` 

\(\left(2x-4\right)-\left(3-x\right)=2x\\ =>2x-4-3+x=2x\\ =>3x-7=2x\\ =>3x-2x=7\\ =>x=7\left(tm\right)\)

TH3: `x<2` 

\(-\left(2x-4\right)+\left(3-x\right)=2x\\ =>-2x+4+3-x=2x\\ =>-3x+7=2x\\ =>2x+3x=7\\ =>5x=7\\ =>x=\dfrac{7}{5}\left(tm\right)\)

Vậy: ...

\(\left|2x-4\right|+\left|3-x\right|=2x\)

Ta có : \(\left|2x-4\right|+\left|3-x\right|\ge\left|2x-4+3-x\right|=\left|x-1\right|\)

\(\Rightarrow\left|x-1\right|=2x\)

\(\)\(\Rightarrow\left\{{}\begin{matrix}2x\ge0\\x-1=2x\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}2x\ge0\\x-1=-2x\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x\ge0\\x=-1\end{matrix}\right.\) (loại) hay \(\left\{{}\begin{matrix}x\ge0\\x=\dfrac{1}{3}\end{matrix}\right.\)

\(\Rightarrow x=\dfrac{1}{3}\)