1+3+5+...+x=36
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



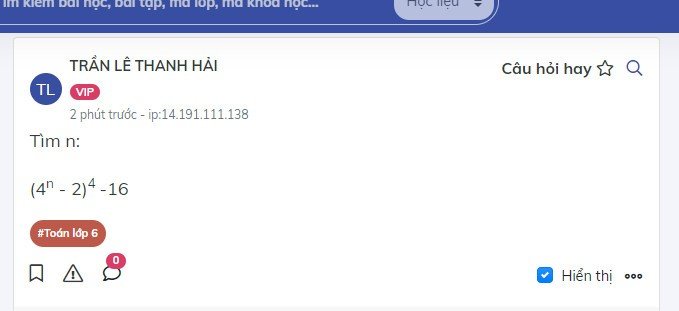
\(A=2^2+2^4+2^6+...+2^{200}\\ 2^2A=2^4+2^6+...+2^{202}\\ 4A-A=\left(2^4+2^6+2^8+...+2^{202}\right)-\left(2^2+2^4+2^6+...+2^{200}\right)\\ 3A=2^{202}-2^2\)
\(=>3A+4=2^{202}-2^2+4=2^{202}-4+4=2^{202}\)
\(=>2^{202}=4^n\\ =>2^{202}=\left(2^2\right)^n\\ =>2^{202}=2^{2n}\\ =>2n=202\\ =>n=101\)

Tỉ số giữa Số học sinh khá và cả lớp là:
\(\dfrac{1}{2}\left(1-\dfrac{1}{4}\right)=\dfrac{1}{2}\cdot\dfrac{3}{4}=\dfrac{3}{8}\)
Số học sinh trung bình chiếm: \(1-\dfrac{3}{8}-\dfrac{1}{4}=\dfrac{5}{8}-\dfrac{2}{8}=\dfrac{3}{8}\)(số học sinh cả lớp)
Số học sinh cả lớp là \(24:\dfrac{3}{8}=24\cdot\dfrac{8}{3}=64\left(bạn\right)\)

1: Sửa đề: Vẽ \(\widehat{x'Ay'}\) là góc đối đỉnh của góc xAy
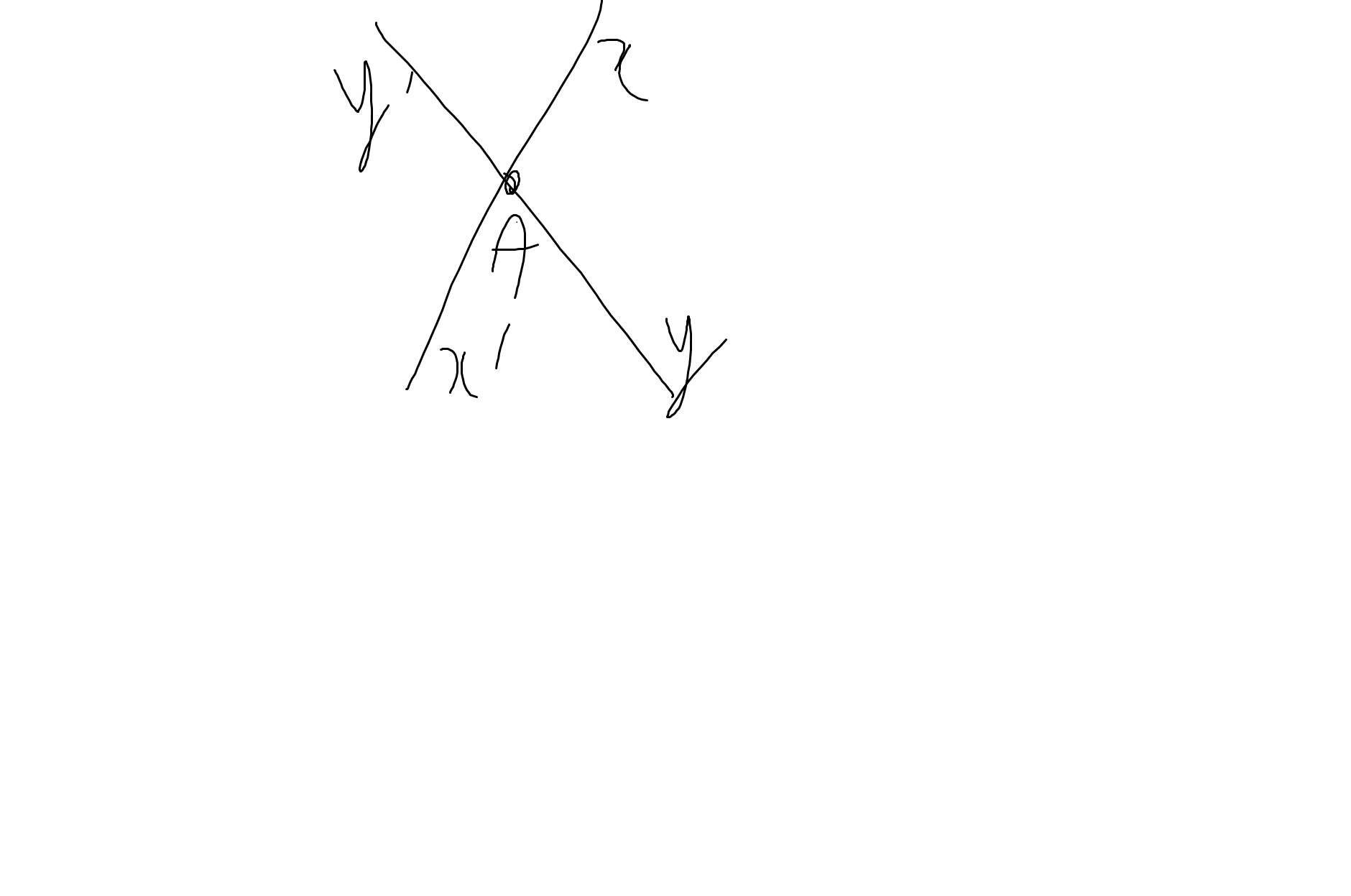
2: Ta có: \(\widehat{xAy}+\widehat{xAy'}=180^0\)(hai góc kề bù)
=>\(\widehat{xAy'}+100^0=180^0\)
=>\(\widehat{xAy'}=80^0\)
Ta có: \(\widehat{xAy}=\widehat{x'Ay'}\)(hai góc đối đỉnh)
mà \(\widehat{xAy}=100^0\)
nên \(\widehat{x'A'y}=100^0\)
Ta có: \(\widehat{xAy'}=\widehat{x'Ay}\)(hai góc đối đỉnh)
mà \(\widehat{xAy'}=80^0\)
nên \(\widehat{x'Ay}=80^0\)
S = \(\dfrac{3}{2}\)+ \(\dfrac{7}{6}\)+\(\dfrac{13}{12}\)+...+\(\dfrac{9901}{9900}\)
Xin giúp với!!!

\(S=\dfrac{3}{2}+\dfrac{7}{6}+\dfrac{13}{12}+...+\dfrac{9901}{9900}\)
\(=1+\dfrac{1}{2}+1+\dfrac{1}{6}+...+1+\dfrac{1}{9900}\)
\(=\left(1+1+1+...+1\right)+\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\right)\)
\(=99+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=99+\left(1-\dfrac{1}{100}\right)=100-\dfrac{1}{100}=\dfrac{10000-1}{100}=\dfrac{9999}{100}\)
S = ( 1+\(\dfrac{1}{2}\) ) + ( 1 + \(\dfrac{1}{6}\) ) + .... + ( 1 + \(\dfrac{1}{9900}\) )
= 9900 + ( \(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + ..... + \(\dfrac{1}{99.100}\) )
= 9900 + ( 1 - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + ..... + \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\) )
= 9900 + 1 - \(\dfrac{1}{100}\)
= 9901 - \(\dfrac{1}{100}\)

a) n + 7 chia hết cho n + 3
=> n + 3 + 4 chia hết cho n + 3
=> 4 chia hết cho n + 3
=> n + 3 ∈ Ư(4) = {1; -1;2; -2; 4; -4}
Mà: n là STN nên n + 3 ≥ 3
=> n + 3 = 4
=> n = 1
b) 2n + 9 chia hết cho n + 1
=> 2n + 2 + 7 chia hết cho n + 1
=> 2(n + 1) + 7 chia hết cho n + 1
=> 7 chia hết cho n + 1
=> n + 1 ∈ Ư(7) = {1; -1; 7; -7}
Mà : n là STN nên n + 1 ≥ 1
=> n + 1 = 1 hoặc n + 1 = 7
=> n = 0 hoặc n = 6
a) Sửa đề: (n+7) chia hết cho (n+3)
\(\left(n+7\right)⋮\left(n+3\right)\\ \Rightarrow\left(n+3+4\right)⋮\left(n+3\right)\)
\(\Rightarrow\)\(4⋮\left(n+3\right)\)
Mà \(n\) là số tự nhiên nên \(n+3\) cũng là số tự nhiên suy ra:
\(\left(n+3\right)\inƯ\left(4\right)=\left\{1,2,4\right\}\)
\(\Rightarrow n\in\left\{-2,-1,1\right\}\)
\(\Rightarrow n=1\) (thỏa mãn điều kiện)
Vậy...
b)
\(\left(2n+9\right)⋮\left(n+1\right)\\\Rightarrow \left(2n+2+7\right)⋮\left(n+1\right)\\ \left[2\left(n+1\right)+7\right]⋮\left(n+1\right)\\ 7⋮\left(n+1\right)\)
Mà \(n\) là số tự nhiên nên \(n+1\) cũng là số tự nhiên suy ra:
\(\left(n+1\right)\inƯ\left(7\right)=\left\{1,7\right\}\)
\(\Rightarrow n\in\left\{0,6\right\}\) (thỏa mãn điều kiện)
Vậy...

\(25< 5^{2x-1}< 5^5\)
\(5^2< 5^{2x-1}< 5^5\)
\(2< 2x-1< 5\)
\(2+1< 2x< 5+1\)
\(3< 2x< 6\)
\(\dfrac{3}{2}< x< 3\)
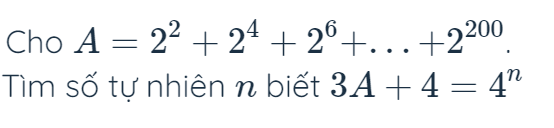
\(1+3+5+...+x=36\\\left[ \left(x-1\right):2+1\right]\cdot\left(x+1\right):2=36\\ \dfrac{x-1+2}{2}\cdot\dfrac{x+1}{2}=36\\ \dfrac{x+1}{2}\cdot\dfrac{x+1}{2}=36\\ \dfrac{\left(x+1\right)^2}{4}=36\\ \left(x+1\right)^2=36\cdot4=144\)
TH1: x + 1 = 12 => x = 11
TH2: x + 1 = -12 => x = -13
Vì: x phải lớn hơn 0 => x = 11
1+3+5+...+x =36
1+3+5+7+9+11 =36