a) Ta có: \(\dfrac{-22}{10}=-\dfrac{22:2}{10:2}=-\dfrac{11}{5}\)

\(\dfrac{11}{-5}=-\dfrac{11}{5}\)

\(\Rightarrow\dfrac{-22}{10}=\dfrac{11}{-5}\)

b) Ta có: \(\dfrac{20}{-52}=-\dfrac{20:4}{52:4}=-\dfrac{5}{13}\)

Mà: \(-\dfrac{5}{13}\ne\dfrac{5}{-14}\)

\(\Rightarrow\dfrac{20}{-52}\ne\dfrac{5}{-14}\)

Ta có: St4 = 14 = 3 + 4 + 7 = st1 + st2 + st3

         ST5 = 25 = 4 + 7 + 14 = st2 + st3 + st4 

Quy luật của dãy số là kể từ số hạng thứ tư trở đi của dãy số, mỗi số hạng trong dãy số bằng tổng của ba số hạng liền kề trước nó.

St6 = st3+ st4 + st5  = 7 + 14 + 25 = 46

ST7 = st4 + st5 + st6 = 14 + 25 + 46 = 85

St8 = st5 + st6 + st7 = 25 + 46 + 85 = 156

Vậy ba số tiếp theo cần điền vào chỗ... của dãy số có quy luật đã cho lần lượt là:

46; 85; 156

3+4

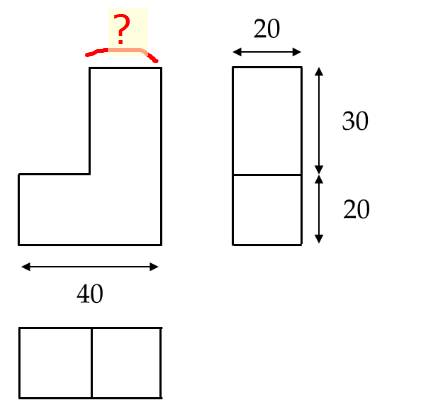
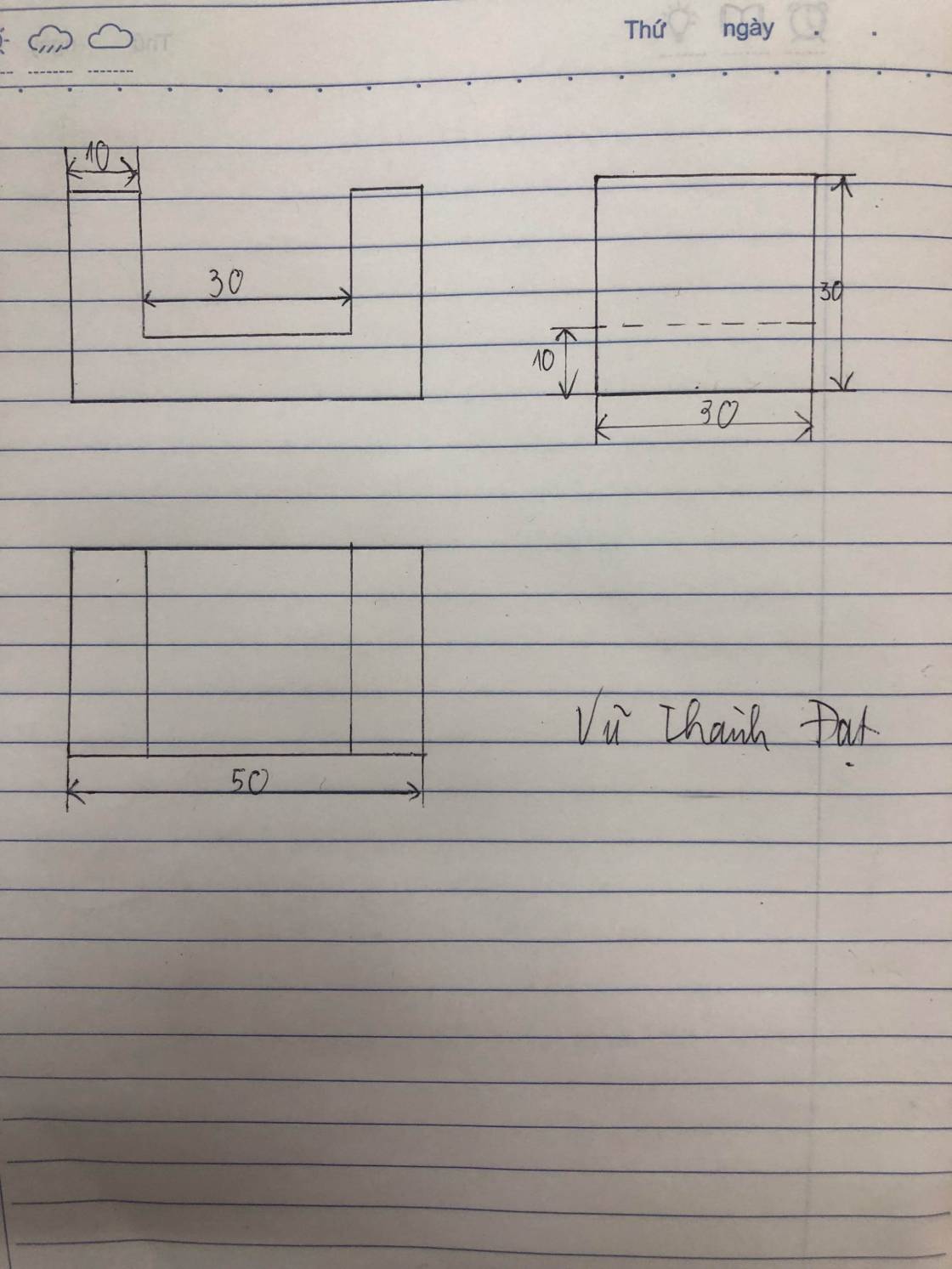
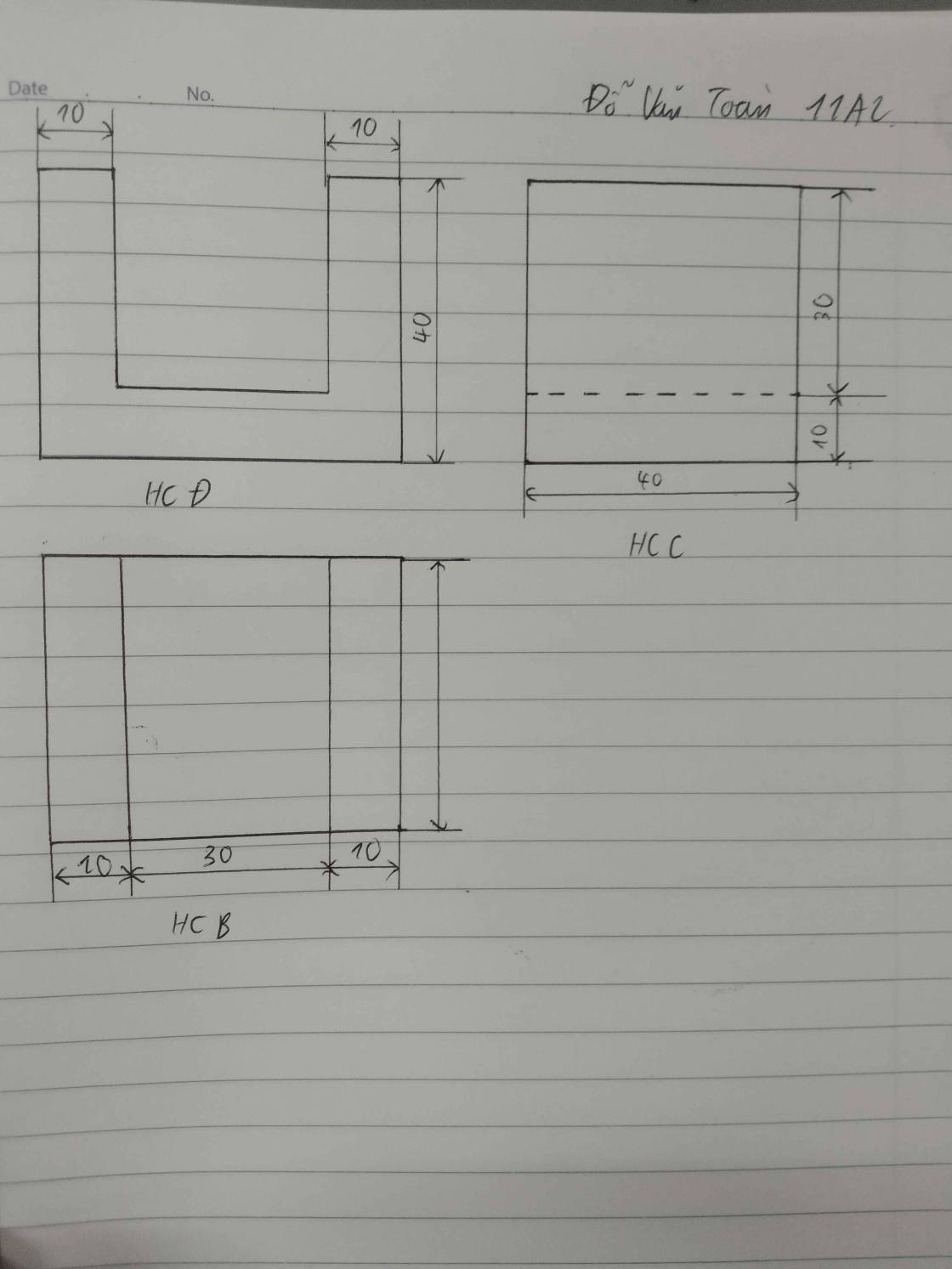
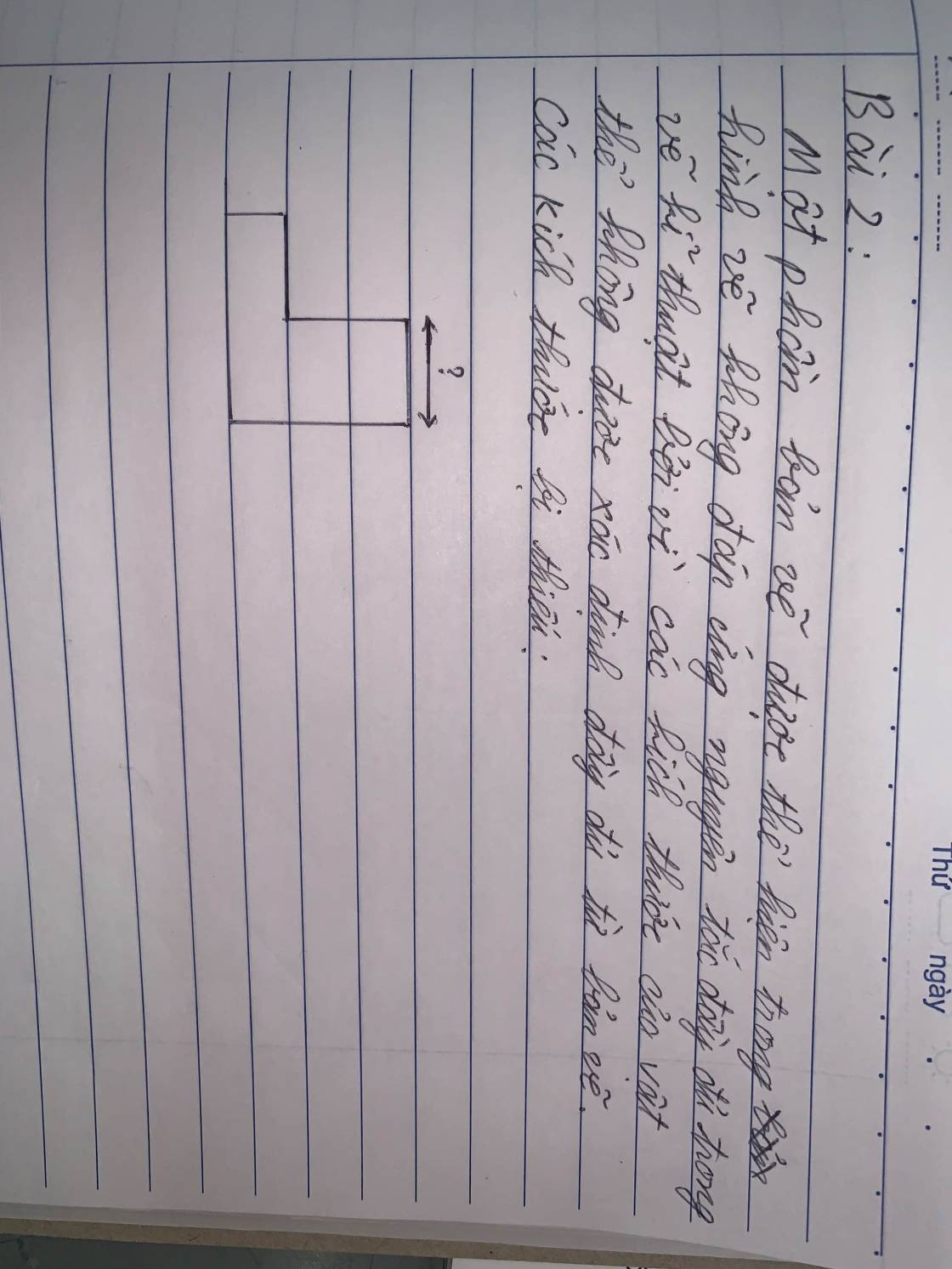
Bản vẽ được thể hiện trong hình vẽ không đáp ứng được nguyên tắc đầy đủ về kĩ thuật là vì bản vẽ thiếu một kích thước nên không thể xác định cụ thể hình ảnh của vật và bản vẽ không có hình khối (3D) mô phỏng hình ảnh của vật 

Kích thước bị thiếu là:

C=(1-5-9+13)+(17-21-25+29)+...+(2013-2017-2021+2025)-2029

C=0+0+0+...+0-2029

C=-2029

C = 1 - 5 - 9 + 13 + 17 - 21 - 25 + 29 + ... + 2013 - 2017 - 2021 + 2025 - 2029

= (1 - 5 - 9 + 13) + (17 - 21 - 25 + 29) + ... + (2001 - 2005 - 2009 + 2013) - 2017 - 2021 + 2025 - 2029

= 0 + 0 + ... + 0 - 4042

= -4042

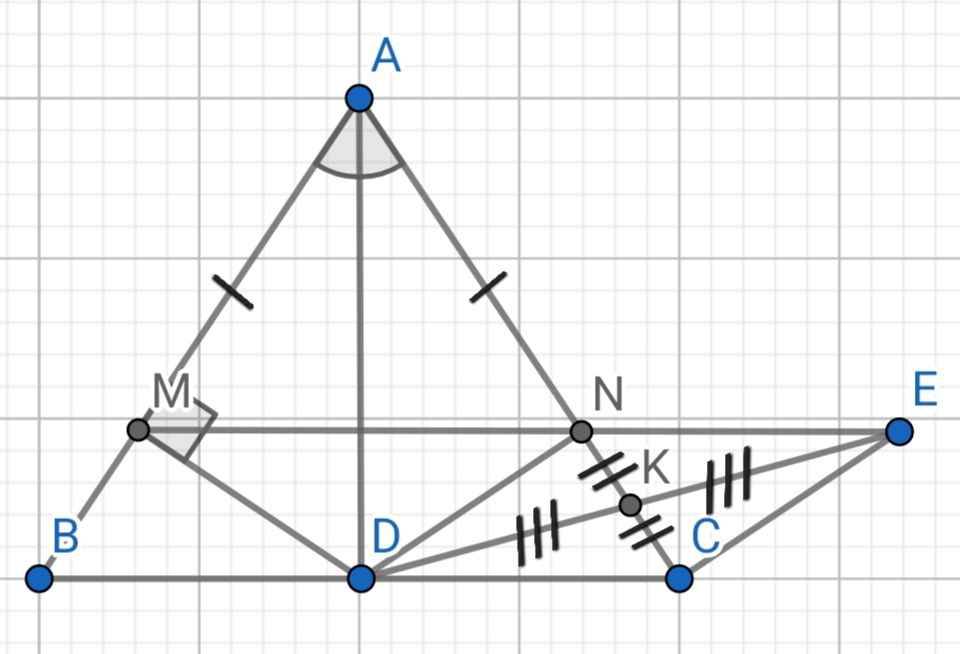 a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

⇒ BD = CD

⇒ D là trung điểm của BC (1)

Do ∆ABD = ∆ACD (cmt)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC (2)

Từ (1) và (2) ⇒ AD là đường trung trực của BC

b) Sửa đề: Chứng minh ∆ADM = ∆ADN

Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

AM = AN (gt)

⇒ ∆ADM = ∆ADN (c-g-c)

⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)

⇒ DN ⊥ AN

⇒ DN ⊥ AC

d) Do K là trung điểm của CN (gt)

⇒ CK = KN

Xét ∆DKC và ∆EKN có:

CK = KN (cmt)

∠DKC = ∠EKN (đối đỉnh)

KD = KE (gt)

⇒ ∆DKC = ∆EKN (c-g-c)

⇒ ∠KDC = ∠KEN (hai góc tương ứng)

Mà ∠KDC và ∠KEN là hai góc so le trong

⇒ EN // CD

⇒ EN // BC (3)

∆AMN có:

AM = AN (gt)

⇒ ∆AMN cân tại A

⇒ ∠AMN = (180⁰ - ∠MAN) : 2

= (180⁰ - ∠BAC) : 2 (4)

∆ABC cân tại A (gt)

⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)

Từ (4) và (5) ⇒ ∠AMN = ∠ABC

Mà ∠AMN và ∠ABC là hai góc đồng vị

⇒ MN // BC (6)

Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

Boy sigma boi 

Lời giải:
a. Diện tích mảnh vườn: 

$(50+70)\times 40:2=2400$ (m²)

Diện tích trồng đu đủ: $2400\times 30:100=720$ (m²)

Có thể trồng được số cây đu đủ là: $720:1,5=480$ (cây) 

b. Diện trích trồng chuối: $2400\times 25:100=600$ (m²)

Số cây chuối trồng được: $600:1=600$ (cây) 

Số cây chuối trồng được nhiều hơn số cây đu đủ là:
$600-480=120$ (cây)

(-5)³.\(x^2\) = - 1125

        \(x^2\) = (-1125) : (-5³)

        \(x^2\) = 9

         \(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)

Vậy \(x\) \(\in\) {-3; 3}

\(\left(-5\right)^3.x^2=-1125\)

\(x^2=-1125:\left(-5\right)^3\)

\(x^2=-1125:\left(-125\right)\)

\(x^2=9\)

\(x^2=3^2\)

\(\Rightarrow\left\{{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

⇒ Vậy \(x\in\left\{{}\begin{matrix}3\\-3\end{matrix}\right.\)

Ta có:

(x + 13) \(⋮\) (x+8)

\(\Rightarrow\) (x + 8 + 5) \(⋮\) (x+8)

\(\Rightarrow\) 5 \(⋮\) (x+8) vì (x+8) \(⋮\) (x+8)

\(\Rightarrow\) x + 8 \(\in\) {1; -1; 5; -5}

\(\Rightarrow\) x \(\in\) {-7; -9; -3; -13}

Vậy: x \(\in\) {-7; -9; -3; -13}

\(\left|2\dfrac{1}{5}-x\right|\)\(+\left|x-\dfrac{1}{5}\right|\)\(+8\dfrac{1}{5}\)\(=1,2\)

\(\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=\dfrac{6}{5}-\dfrac{41}{5}\)

\(\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=\dfrac{-36}{5}\) (vô lý vì \(\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|\ge0\))

Vậy: Không tìm được giá trị x thoả mãn.