Bài 1: Bài thơ "Những cánh buồm" đã gieo vào lòng thế hệ trẻ những ước mơ bay bổng để vươn tới chiếm lĩnh chinh phục vũ trụ. Nó động viên chúng ta phấn đấu không ngừng để vươn tới tầm cao của thời đại.. Vậy ước mơ của con là gì? Con sẽ làm phấn đấu như thế nào để chinh phục ước mơ ấy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
17 tháng 4 2024
a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có
PN chung
\(\widehat{KNP}=\widehat{HPN}\)
Do đó: ΔKNP=ΔHPN
b: Ta có: ΔKNP=ΔHPN
=>\(\widehat{KPN}=\widehat{HNP}\)
=>\(\widehat{ENP}=\widehat{EPN}\)
=>ΔENP cân tại E
c: Xét ΔMEN và ΔMEP có
ME chung
EN=EP(ΔENP cân tại E)
MN=MP
Do đó: ΔMEN=ΔMEP
=>\(\widehat{NME}=\widehat{PME}\)
=>ME là phân giác của góc NMP
17 tháng 4 2024
a: 45p=0,75h
Độ dài quãng đường từ Long An về TPHCM là:
\(0,75\times72=54\left(km\right)\)
b: Vận tốc của xe máy là: \(72\times\dfrac{3}{8}=27\left(\dfrac{km}{h}\right)\)
Thời gian xe máy đi hết quãng đường là:
54:27=2(giờ)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 4 2024
Giải:
a; 45 phút = \(\dfrac{3}{4}\) giờ
Quãng đường từ Long An về Thành Phố Hồ Chí Minh là:
72 x \(\dfrac{3}{4}\) = 54 (km)
b; Cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian nên thời gian ô tô đi từ A đến B là:
\(\dfrac{3}{4}\) : \(\dfrac{3}{8}\) = 2 (giờ)
Đáp số: a; 54 km
b; 2 giờ
TD
1
17 tháng 4 2024
Thời gian ô tô đã đi là:
14h-10h45p-25p
=14h-10h70p
=14h-11h10p
=2h50p
A
1
17 tháng 4 2024
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
\(\left|P\right|+P=0\)
=>|P|=-P
=>P<=0
=>\(\dfrac{3\sqrt{x}}{\sqrt{x}-3}< =0\)
=>\(\dfrac{\sqrt{x}}{\sqrt{x}-3}< =0\)
=>\(0< =\sqrt{x}< 3\)
=>\(0< =x< 9\)
17 tháng 4 2024
Xe máy đi được 45km trong 1 giờ
=>Vận tốc của xe máy là 45:1=45(km/h)
17 tháng 4 2024
Bài 5:
a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m-9=2\\2\ne4\left(đúng\right)\end{matrix}\right.\)
=>m-9=2
=>m=11
b: (d3) có hệ số góc bằng 5 thì m+3=5
=>m=2
=>(d3): y=5x+2n-5
Để (d3) cắt (d) tại một điểm nằm trên trục hoành thì:
\(\left\{{}\begin{matrix}5\ne2\\\dfrac{-2n+5}{5}=\dfrac{-4}{2}=-2\end{matrix}\right.\)
=>\(-2n+5=-10\)
=>-2n=-15
=>\(n=7,5\)
c: Để (d) cắt (d3) tại một điểm trên trục tung thì:
\(\left\{{}\begin{matrix}3m+2\ne2\\4=-6m+7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne0\\m=\dfrac{1}{2}\end{matrix}\right.\)
=>m=1/2
Bài 4:
a: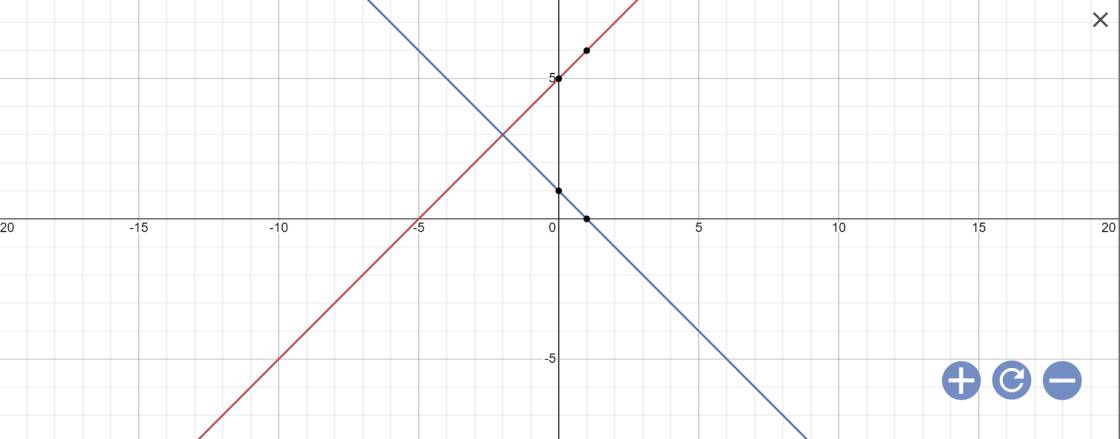 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}x+5=-x+1\\y=x+5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=-4\\y=x+5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=-2+5=3\end{matrix}\right.\)
Vậy: A(-2;3)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\x+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-5\\y=0\end{matrix}\right.\)
Vậy: B(-5;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
=>C(1;0)
A(-2;3); B(-5;0); C(1;0)
\(AB=\sqrt{\left(-5+2\right)^2+\left(0-3\right)^2}=3\sqrt{2}\)
\(AC=\sqrt{\left(1+2\right)^2+\left(0-3\right)^2}=3\sqrt{2}\)
\(BC=\sqrt{\left(1+5\right)^2+\left(0-0\right)^2}=6\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\sqrt{2}\cdot3\sqrt{2}=9\)