Quy đồng mẫu các phân thức sau:(có thể tính luôn càng tốt ạ)
a) \(\dfrac{a+x}{a^2x}\);\(\dfrac{x+b}{x^2b}\);\(\dfrac{b+a}{b^2a}\)
b) \(\dfrac{a-x}{6x^2-ax-2a^2}\);\(\dfrac{a+x}{3x^2+4ax-4a^2}\)
c) \(\dfrac{1-2x}{2x}\) + \(\dfrac{2x}{2x-1}\) + \(\dfrac{1}{2x-4x^2}\)
Mn giúp mik vs nhaaa! Tầm trc cmai nhoaaa!
Thanks mn trc ạ!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



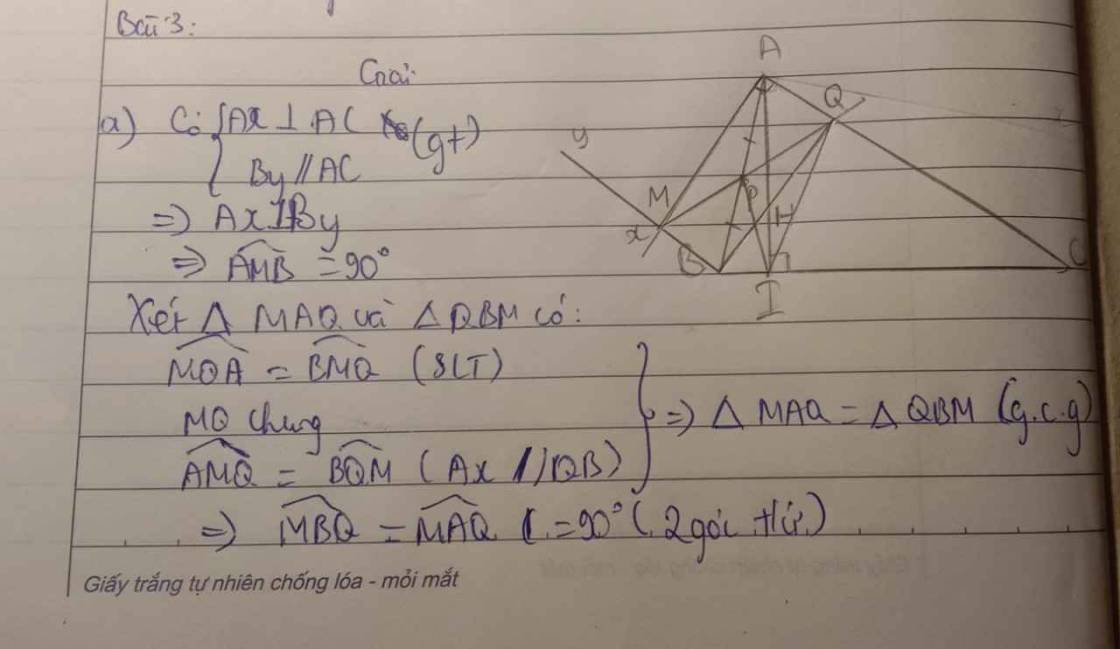
a) Ta có: ��⊥��Ax⊥AC và ��By // ��AC
=> ��⊥��Ax⊥By ⇒���^=90∘
⇒Góc AMB = 90 độ
Xét Δ���ΔMAQ và Δ���ΔQBM có
���^=���^Góc MQA = góc BQM (so le trong);
��MQ là cạnh chung;
���^=���^Góc AMQ = góc BQM(Ax//QB)
Suy ra Δ���= Δ���ΔMAQ= ΔQBM (g-c-g)
Suy ra góc MBQ = góc MAQ= 90 độ (2 góc tương ứng)
Xét tứ giác AMBQ có
Góc QAM = góc AMB = góc MBQ = 90 độ
=> tứ giác ����AMBQ là hình chữ nhật.
b) Do tứ giác ����AMBQ là hình chữ nhật
Mà P là trung điểm AB
=>P là trung điểm của MQ; AB = MQ
=> PQ = 1/2 AB (1)
Xét tam giác AIB vuông tại I và có IP là đường trung tuyến
=> IP = 1/2 AB(2)
Từ (1) và (2)
=> QP =IP
=> Tam giác PQI cân tại P

Diện tích xung quanh của kho chứa:
\(S_{xq}=p\cdot d=\dfrac{12+12+12}{2}\cdot8=144\left(m^2\right)\)
Diện tích cần sơn thực tế:
\(S_s=S_{xq}-S_c=144-5=139\left(m^2\right)\)
Số tiền cần dùng để hoàn thành việc sơn là:
\(T=S_s\cdot30000=4170000\left(đ\right)\)

Áp dụng BĐT Cô-si cho 3 số dương \(x^2,y^2,z^2\) , ta có:\(x^2+y^2+z^2\ge3\sqrt[3]{\left(xyz\right)^2}\)
\(\Leftrightarrow\left(xyz\right)^2\le\dfrac{\left(x^2+y^2+z^2\right)^3}{27}\) \(=\dfrac{1}{27}\)
\(\Leftrightarrow-\dfrac{1}{3\sqrt{3}}\le xyz\le\dfrac{1}{3\sqrt{3}}\)
Vậy \(max_{xyz}=\dfrac{1}{3\sqrt{3}}\). Dấu "=" xảy ra khi \(x^2=y^2=z^2\)
\(\Rightarrow\left(x,y,z\right)=\left(\dfrac{1}{\sqrt{3}},\dfrac{1}{\sqrt{3}},\dfrac{1}{\sqrt{3}}\right)\) hoặc \(\left(\dfrac{1}{\sqrt{3}},-\dfrac{1}{\sqrt{3}},-\dfrac{1}{\sqrt{3}}\right)\) và các hoán vị.

\(a)\left(x^2+2x\right)\left(x^2+2x+4\right)+3\)
Để đơn giản hơn cũng như là dễ nhìn hơn thì ta :
Đặt : \(x^2+2x=a\)
Do đó ta có đa thức :
\(a.\left(a+4\right)+3=a^2+4a+3\)
\(=a^2+a+3a+3\)
\(=a\left(a+1\right)+3\left(a+1\right)\)
\(=\left(a+1\right)\left(a+3\right)\)
\(=\left(x^2+2x+1\right)\left(x^2+2x+3\right)\)
\(=\left(x+1\right)^2.\left(x^2+2x+3\right)\)
Hoặc bạn có thể đặt \(x^2+2x+2=t\)
Thì \(P=\left(x^2+2x\right)\left(x^2+2x+4\right)+3\)
\(P=\left(t-2\right)\left(t+2\right)+3\)
\(P=t^2-4+3\)
\(P=t^2-1\)
\(P=\left(t-1\right)\left(t+1\right)\)
\(P=\left(x^2+2x+1\right)\left(x^2+2x+3\right)\)
\(P=\left(x+1\right)^2\left(x^2+2x+3\right)\)
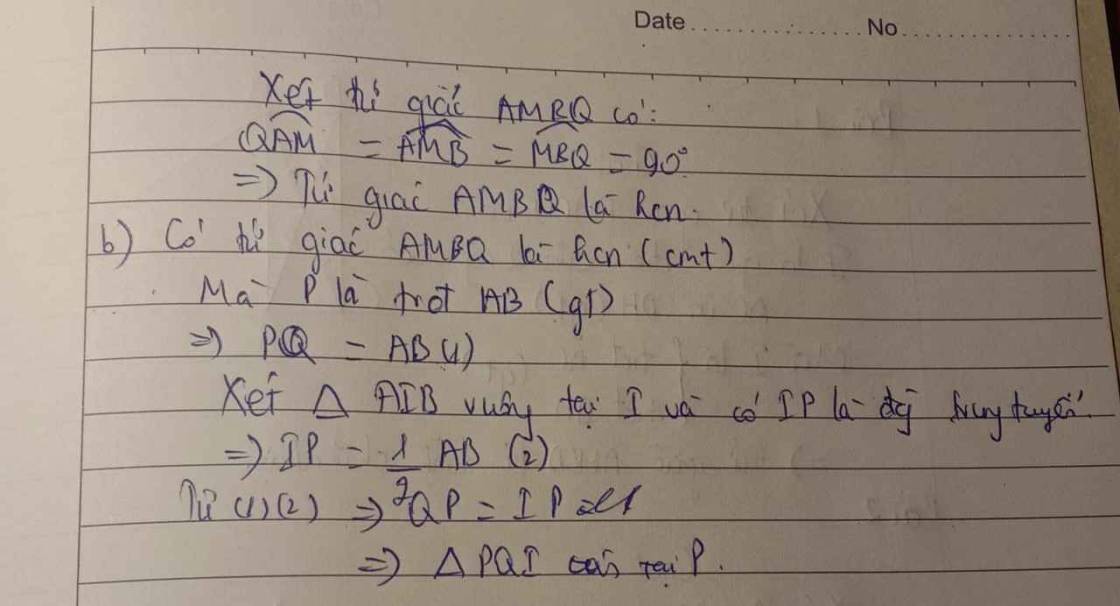

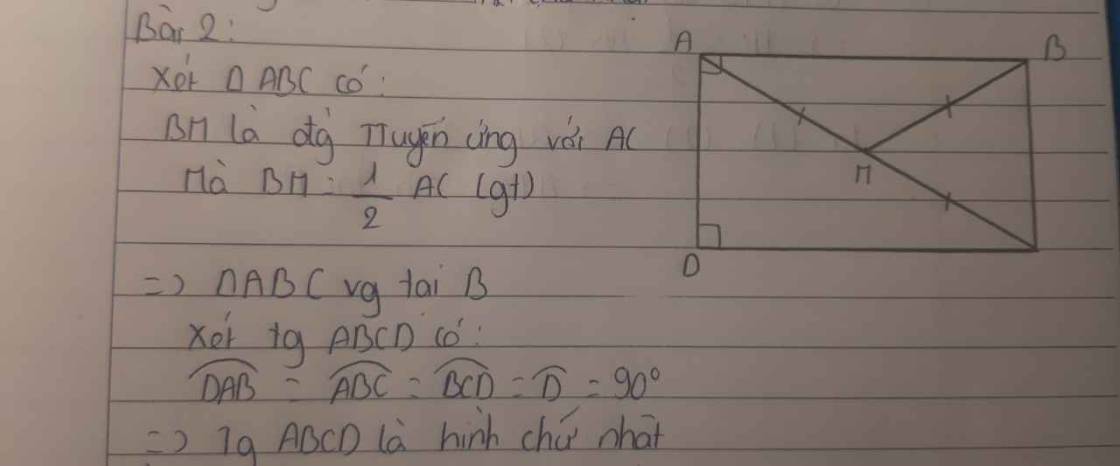


Mn giúp mik vs ạ