
cứu là hộ câu 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>PA\(\perp\)BD tại A
Xét (O) có
ΔCIB nội tiếp
CB là đường kính
Do đó: ΔCIB vuông tại I
Xét tứ giác ADHC có \(\widehat{DAC}+\widehat{DHC}=90^0+90^0=180^0\)
nên ADHC là tứ giác nội tiếp
b: Xét ΔDBP có
PA,BH là các đường cao
PA cắt BH tại C
Do đó: C là trực tâm của ΔDBP
=>DC\(\perp\)BP
mà CI\(\perp\)BP
mà DC,CI có điểm chung là C
nên D,C,I thẳng hàng
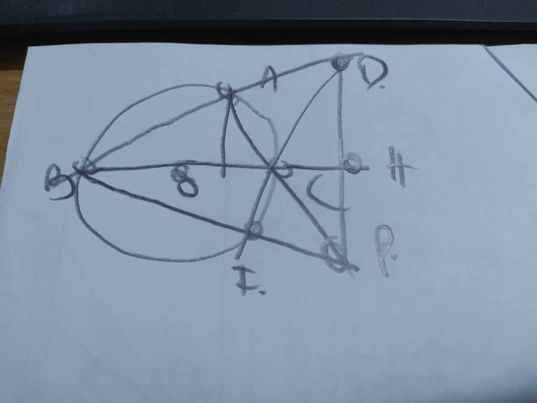
| GT | (O) có đường kính BC \(A\in\left(O\right);AP>AC;P\in AC\) PB\(\cap\)(O)={I} PH\(\perp\)BC tại H, PH cắt BA tại D |
| KL | a: ACHD nội tiếp b: D,C,I thẳng hàng |

Câu 1
∆' = [-(m + 1)]² - m(m + 2)
= m² + 2m + 1 - m² - 2m
= 1 > 0
Phương trình luôn có hai nghiệm phân biệt
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = 2(m + 1)/m
x₁x₂ = (m + 2)/m
Câu 3:
∆' = 4 - (2 - √3)(2 + √2)
= 4 - 4 - 2√2 + 2√3 + √6
= √6 + 2√3 - 2√2 > 0
Phương trình luôn có hai nghiệm phân biệt
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = -4/(2 - √3)= -8 - 2√3
x₁x₂ = (2 + √2)/(2 - √3) = (2 + √2)(2 + √3)

D và E cùng nhìn BC dưới 1 góc vuông \(\Rightarrow BCDE\) nội tiếp
\(\Rightarrow\widehat{BDE}=\widehat{BCE}\) (cùng chắn BE)
Lại có \(\widehat{BCE}=\widehat{BD'E'}\) (cùng chắn BE' của (O))
\(\Rightarrow\widehat{BDE}=\widehat{BD'E'}\)
\(\Rightarrow DE||D'E'\) (hai góc đồng vị bằng nhau)

Pt hoành độ giao điểm: \(x^2=2x-m+3\) (1)
\(\Leftrightarrow x^2-2x+m-3=0\)
\(\Delta'=1-\left(m-3\right)>0\Rightarrow m< 4\)
Theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Do \(x_1\) là nghiệm của (1) nên: \(x_1^2=2x_1-m+3\)
Thế vào:
\(x_1^2+12=2x_2-x_1x_2\)
\(\Leftrightarrow2x_1-m+3+12=2x_1-\left(m-3\right)\)
\(\Leftrightarrow x_1-x_2=6\)
\(\Rightarrow x_2=x_1-6\)
Thế vào \(x_1+x_2=2\Rightarrow x_1+x_1-6=2\)
\(\Rightarrow x_1=4\Rightarrow x_2=-2\)
Thay vào \(x_1x_2=m-3\Rightarrow m-3=-8\)
\(\Rightarrow m=-5\) (thỏa mãn)

Hai đường tròn cắt nhau tại tối đa 2 điểm, do đó 4 đường tròn cắt nhau tại tối đa là:
\(2.3+2.2+2.1=12\) điểm

a: Thay x=16 vào B, ta được:
\(B=\dfrac{16+3}{3+4}=\dfrac{19}{7}\)
b: \(A=\left(\dfrac{x+3\sqrt{x}-2}{x-9}-\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\left(\dfrac{x+3\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{1}{\sqrt{x}+3}\right)\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{x+3\sqrt{x}-2-\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
c: \(M=B:A=\dfrac{x+3}{\sqrt{x}+3}:\dfrac{\sqrt{x}+1}{\sqrt{x}+3}=\dfrac{x+3}{\sqrt{x}+1}\)
\(=\dfrac{x-1+4}{\sqrt{x}+1}=\sqrt{x}-1+\dfrac{4}{\sqrt{x}+1}\)
\(=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}-2\)
=>\(M>=2\cdot\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}-2=2\cdot2-2=2\)
Dấu '=' xảy ra khi \(\left(\sqrt{x}+1\right)^2=4\)
=>\(\sqrt{x}+1=2\)
=>x=1(nhận)

a: Xét tứ giác BCEF có \(\widehat{BEC}=\widehat{BFC}=90^0\)
nên BCEF là tứ giác nội tiếp đường tròn đường kính BC
tâm I là trung điểm của BC

Lời giải:
Lấy PT(1) + 3PT(2) ta được:
$-3x+2y+3(x-3y)=-11+3.6$
$\Leftrightarrow -7y=7$
$\Leftrightarrow y=-1$
Khi đó:
$x=6+3y=6+3(-1)=6-3=3$
Vậy HPT có nghiệm $(x,y)=(3,-1)$
bài 1:
a: \(\left\{{}\begin{matrix}3x+2y=5\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+2y=5\\4x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=1\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=2-2x=2-2\cdot\left(-1\right)=4\end{matrix}\right.\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=5\\x_1x_2=\dfrac{c}{a}=2\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=5^2-2\cdot2=25-4=21\)