
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\dfrac{2}{3}+\dfrac{1}{3}:x=\dfrac{4}{3}\\ =>\dfrac{1}{3}:x=\dfrac{4}{3}-\dfrac{2}{3}\\ =>\dfrac{1}{3}:x=\dfrac{2}{3}\\ =>x=\dfrac{1}{3}:\dfrac{2}{3}=\dfrac{1}{2}\\ 2,\dfrac{4}{5}+\dfrac{1}{3}:x=\dfrac{2}{3}\\ =>\dfrac{1}{3}:x=\dfrac{2}{3}-\dfrac{4}{5}=-\dfrac{2}{15}\\ =>x=\dfrac{1}{3}:\dfrac{-2}{15}=\dfrac{-5}{2}\\ 3,\dfrac{2}{3}+\dfrac{5}{2}:x=\dfrac{3}{4}\\ =>\dfrac{5}{2}:x=\dfrac{3}{4}-\dfrac{2}{3}\\ =>\dfrac{5}{2}:x=\dfrac{1}{12}\\ =>x=\dfrac{5}{2}:\dfrac{1}{12}=30\)

a: Ta có: \(BF=FC=\dfrac{BC}{2}\)
\(AE=ED=\dfrac{AD}{2}\)
mà BC=AD
nên BF=FC=AE=ED
Xét tứ giác BFDE có
BF//DE
BF=DE
Do đó: BFDE là hình bình hành
=>EB=DF(3)
b: Ta có: BFDE là hình bình hành
=>BD cắt FE tại trung điểm của mỗi đường
mà O là trung điểm của FE
nên O là trung điểm của BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của AC
=>AC,BD,EF đồng quy tại O
c: Xét ΔABD có
BE,AO là các đường trung tuyến
BE cắt AO tại I
Do đó: I là trọng tâm của ΔABD
=>\(BI=\dfrac{2}{3}BE\left(1\right)\)
Xét ΔDBC có
DF,CO là các đường trung tuyến
DF cắt CO tại K
Do đó: K là trọng tâm của ΔDBC
=>\(DK=\dfrac{2}{3}DF\left(2\right)\)
Từ (1),(2),(3) suy ra BI=DK
Xét tứ giác BIDK có
BI//DK
BI=DK
Do đó: BIDK là hình bình hành
=>BK=DI
Xét ΔBCI có
F là trung điểm của CB
FK//BI
Do đó: K là trung điểm của CI
=>CK=KI
Xét ΔAKD có
E là trung điểm của AD
EI//KD
Do đó: I là trung điểm của AK
=>AI=IK
Do đó: AI=IK=KC

2) Đổi: 14,4 m = 144dm, 7,2m = 72dm, 20cm = 2dm
Diện tích căn phòng là:
144 x 72 = 10368 `(dm^2)`
Diện tích mỗi viên gạch là:
2 x 2 = 4 `(dm^2)`
Số viên gạch cần dùng là:
10368 : 4 = 2592 (viên)
ĐS: ...
Bài 1: Thời gian người đó đi từ A đến B là:
10h-6h15p-15p=10h-6h30p=3h30p=3,5(giờ)
Độ dài quãng đường từ tỉnh A đến tỉnh B là:
3,5x55=192,5(km)

Sửa lại Gia đình bà Vân gồm 4 người lớn và 3 trẻ em thanh toán \(110000\) đồng thành \(1100000\) đồng
Gọi giá buffet của người lớn và trẻ em lần lượt là \(x;y\left(x;y>0\right)\)
Tổng số tiền ông Khanh : \(5x+5y=1500000\)
\(\Rightarrow x+y=300000\left(2\right)\)
Tổng số tiền nhà bà Vân : \(4x+3y=1100000\left(2\right)\)
\(\left(1\right);\left(2\right)\) ta có HPT :
\(\left\{{}\begin{matrix}x+y=300000\\4x+3y=1100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+4y=1200000\\4x+3y=1100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=300000\\y=100000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=200000\\y=100000\end{matrix}\right.\)
Vậy giá buffet của người lớn và trẻ em lần lượt là \(200000\left(đồng\right);100000\left(đồng\right)\)
Em kiểm tra lại đề, rất có thể ở dữ liệu nhà bà Vân em ghi thiếu 1 số 0 ở con số 110 000, lẽ ra phải là 1 100 000 mới hợp lý



\(499^2+499+500\)
\(=499^2+499+\left(499+1\right)\)
\(=499^2+2.499+1\)
\(=\left(499+1\right)^2\)
\(=500^2\)
\(=2500\)

\(499^2+499+500\)
\(=\left(500-1\right)^2+\left(500-1\right)+500\)
\(=500^2-2.100+1+500-1+500\)
\(=500^2=2500\)

a. Đọc là: hai tư phẩy ba trăm bốn mươi lăm
b.
Chữ số 3 có giá trị \(30000\)
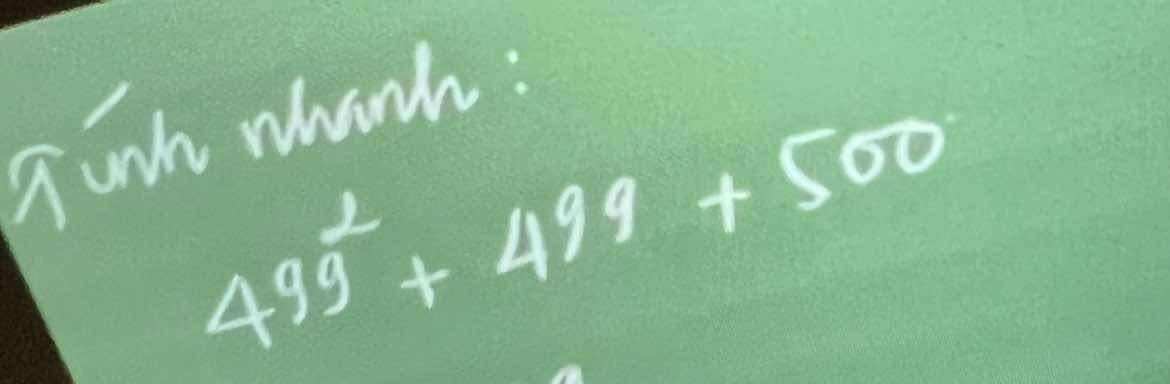


a: Trên tia Oa, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+3=5
=>MN=2(cm)
b: Trên tia Oa, ta có: ON<OP
nên N nằm giữa O và P
=>ON+NP=OP
=>NP+5=7
=>NP=2(cm)
Trên tia Oa, ta có: OM<OP
nên M nằm giữa O và P
=>OM+MP=OP
=>MP+3=7
=>MP=4(cm)
Vì MN+NP=MP
nên N nằm giữa M và P
Ta có: N nằm giữa M và P
mà NM=NP(=2cm)
nên N là trung điểm của MP
c: Vì O là trung điểm của MQ
nên \(MQ=2\cdot MO=2\cdot3=6\left(cm\right)\)
MQ=6cm
ON=5cm
Do đó: MQ>ON