
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét ΔNBC và ΔNEA có
NB=NE
\(\widehat{BNC}=\widehat{ENA}\)(hai góc đối đỉnh)
NC=NE
Do đó: ΔNBC=ΔNEA
=>\(\widehat{NBC}=\widehat{NEA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BC//AE
Ta có: ΔNBC=ΔNEA
=>BC=EA
Xét ΔPAF và ΔPBC có
PA=PB
\(\widehat{APF}=\widehat{BPC}\)(hai góc đối đỉnh)
PF=PC
Do đó: ΔPAF=ΔPBC
=>\(\widehat{PAF}=\widehat{PBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
ta có: ΔPAF=ΔPBC
=>AF=BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF(=BC)
nên A là trung điểm của EF

a: Xét ΔCHO vuông tại H và ΔCFO vuông tại F có
CO chung
\(\widehat{HCO}=\widehat{FCO}\)
Do đó: ΔCHO=ΔCFO
=>CH=CF
=>ΔCHF cân tại C

a: Ta có: ΔBAD vuông tại A
=>BD là cạnh huyền
=>BD>BA
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC tại E
Ta có: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
Do đó: ΔDAF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của FC(1)
Ta có: NF=NC
=>N nằm trên đường trung trực của CF(2)
ta có: BA+AF=BF
BE+EC=BC
mà BA=BE và AF=EC
nên BF=BC
=>B nằm trên đường trung trực của CF(3)
Từ (1),(2),(3) suy ra B,D,N thẳng hàng

Gọi tuổi hiện nay của em là x(tuổi)
(ĐIều kiện: x>0)
Tuổi anh hiện nay là x+8(tuổi)
Tuổi anh cách đây 5 năm là x+8-5=x+3(tuổi)
Tuổi em sau đây 8 năm là x+8(tuổi)
Theo đề, ta có: \(x+3=\dfrac{3}{4}\left(x+8\right)\)
=>\(x+3=\dfrac{3}{4}x+6\)
=>\(\dfrac{1}{4}x=3\)
=>x=12(nhận)
Vậy: Tuổi em hiện nay là 12 tuổi, tuổi anh hiện nay là 12+8=20 tuổi

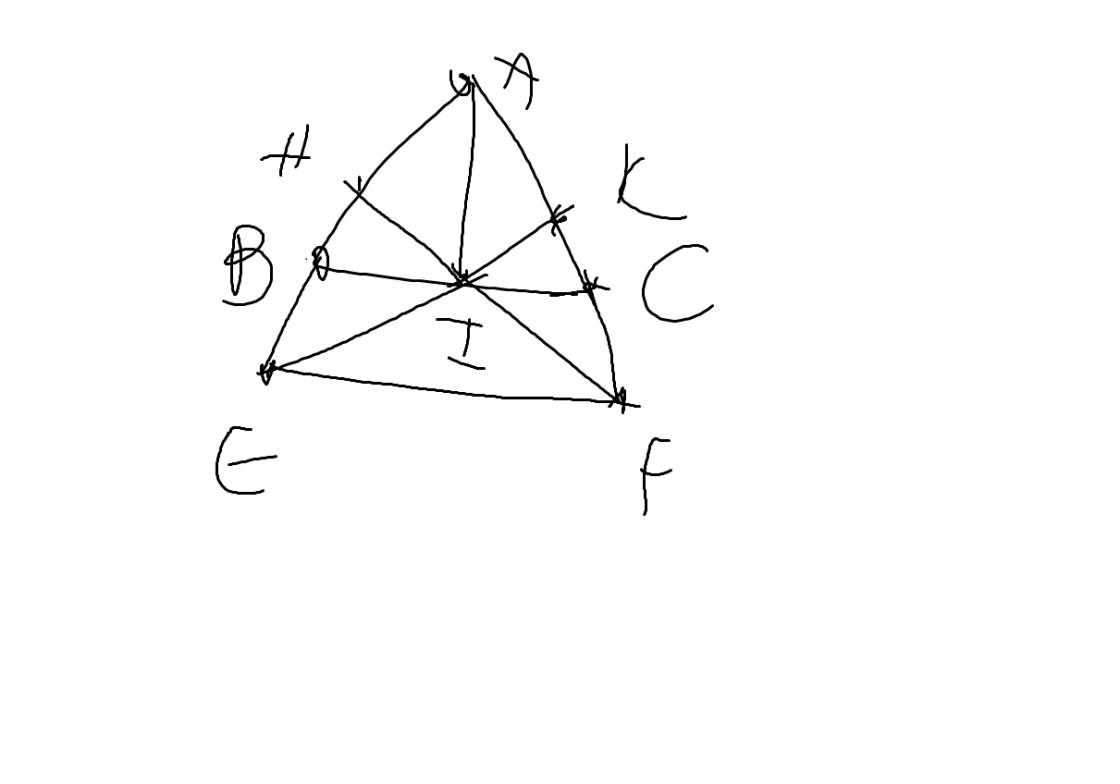
a: Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔIHB=ΔIKC
b: Ta có: ΔIHB=ΔIKC
=>IB=IC
mà IC>IK(ΔIKC vuông tại K)
nên IB>IK
c:
Ta có: ΔIHB=ΔIKC
=>IH=IK
Xét ΔHIE vuông tại H và ΔKIF vuông tại K có
IH=IK
\(\widehat{HIE}=\widehat{KIF}\)(hai góc đối đỉnh)
Do đó; ΔHIE=ΔKIF
=>HE=KF
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Ta có: AH+HE=AE
AK+KF=AF
mà AH=AK và HE=KF
nên AE=AF
=>ΔAEF cân tại A
d: Xét ΔAEF có \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\)
nên HK//EF
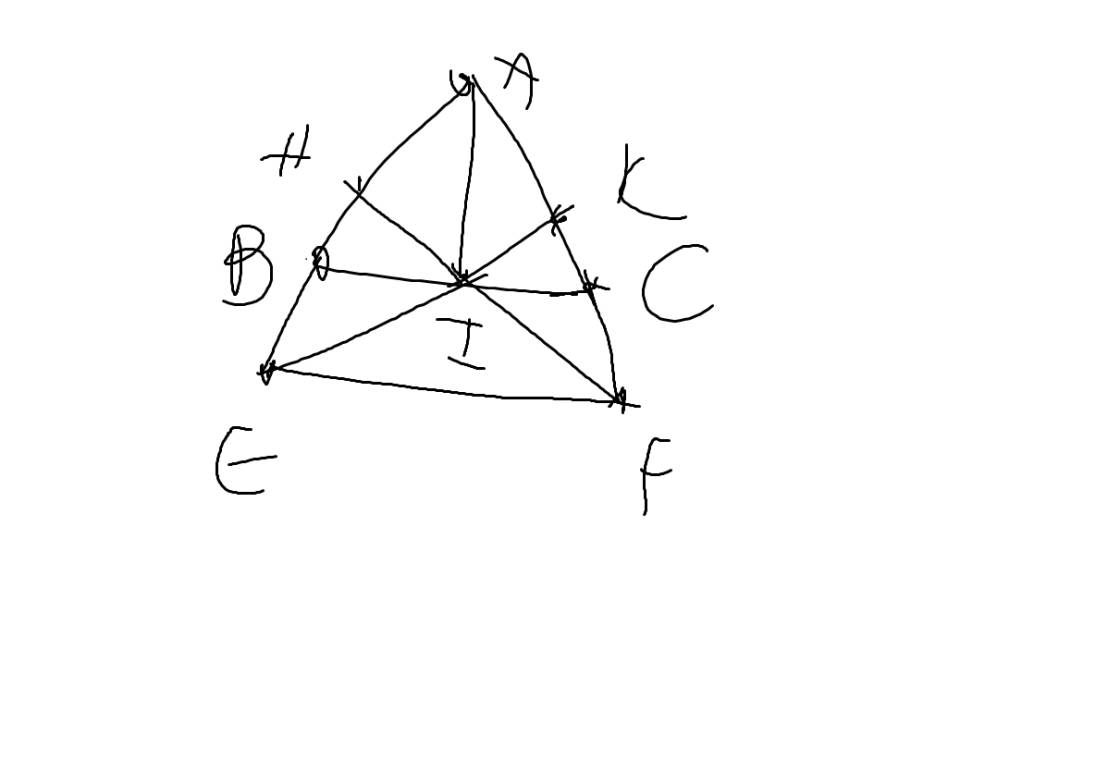

a: Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔIHB=ΔIKC
b: Ta có: ΔIHB=ΔIKC
=>IB=IC
mà IC>IK(ΔIKC vuông tại K)
nên IB>IK
c:
Ta có: ΔIHB=ΔIKC
=>IH=IK
Xét ΔHIE vuông tại H và ΔKIF vuông tại K có
IH=IK
\(\widehat{HIE}=\widehat{KIF}\)(hai góc đối đỉnh)
Do đó; ΔHIE=ΔKIF
=>HE=KF
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Ta có: AH+HE=AE
AK+KF=AF
mà AH=AK và HE=KF
nên AE=AF
=>ΔAEF cân tại A
d: Xét ΔAEF có \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\)
nên HK//EF

\(\dfrac{-25}{5-x}=\dfrac{5-x}{-16}\)
\(\Rightarrow\dfrac{-25}{-\left(x-5\right)}=\dfrac{-\left(x-5\right)}{-16}\)
\(\Rightarrow\dfrac{25}{x-5}=\dfrac{x-5}{16}\)
\(\Rightarrow\left(x-5\right)^2=25\cdot16\)
\(\Rightarrow\left(x-5\right)^2=400\)
\(\Rightarrow\left(x-5\right)^2=20^2\)
TH1: \(x-5=20\)
\(\Rightarrow x=25\)
TH2: \(x-5=-20\)
\(\Rightarrow x=-15\)
Vậy: ...

c: Ta có: ΔAEM vuông tại A
=>\(\widehat{AEM}< 90^0\)
mà \(\widehat{CEM}+\widehat{AEM}=180^0\)(hai góc kề bù)
nên \(\widehat{CEM}>90^0\)
Xét ΔCEM có \(\widehat{CEM}>90^0\)
nên CM là cạnh lớn nhất trong ΔCEM
=>CM>ME
e: Xét ΔCAB có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{1}{2}\)
=>CD=2BD

a) B(x) = 3x² - x³ + 2x² + 4x - 5 + 2x³
= (3x² + 2x²) + (-x³ + 2x³) + 4x - 5
= 5x² + x³ + 4x - 5
=> Vậy, đa thức B(x) sau khi thu gọn là B(x) = x³ + 5x² + 4x - 5.
b) Bậc của đa thức B(x) là 3 và hệ số cao nhất của đa thức B(x) là 1.
Lời giải:
a. $B(x)=(-x^3+2x^3)+(3x^2+2x^2)+4x-5$
$=x^3+5x^2+4x-5$
b.
Bậc của đa thức: $3$
Hệ số cao nhất: $1$ (chính là hệ số gắn với $x^3$)


