\(\dfrac{2xX-4,36}{0,125}=0,25x42,9-11,7x0,25+0,25x0,8\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


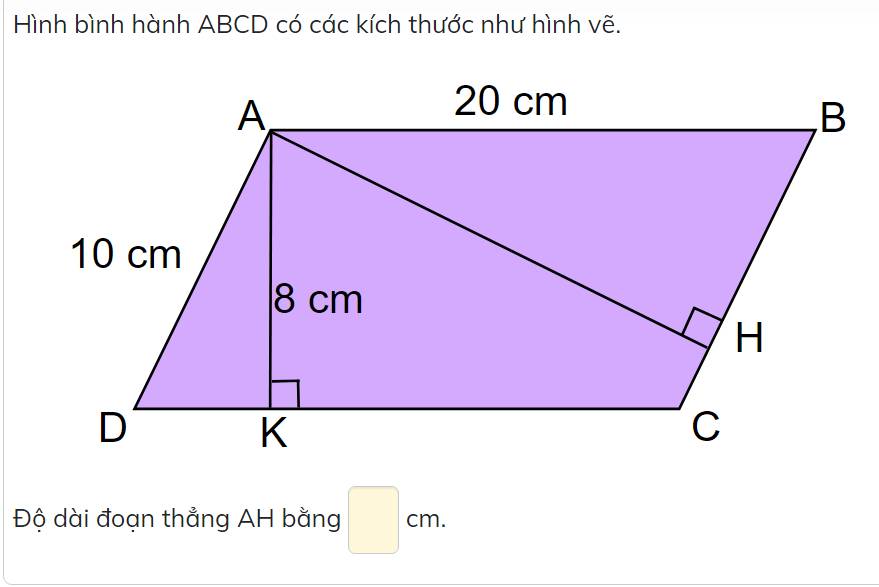
\(S_{ABCD}=\dfrac{\left(AB+CD\right).AK}{2}=\dfrac{\left(20+20\right).8}{2}=160cm^2\)
Mặt khác
\(S_{ABCD}=\dfrac{\left(AD+BC\right).AH}{2}=\dfrac{\left(10+10\right).AH}{2}=160cm^2\)
\(\Rightarrow AH=16cm\)

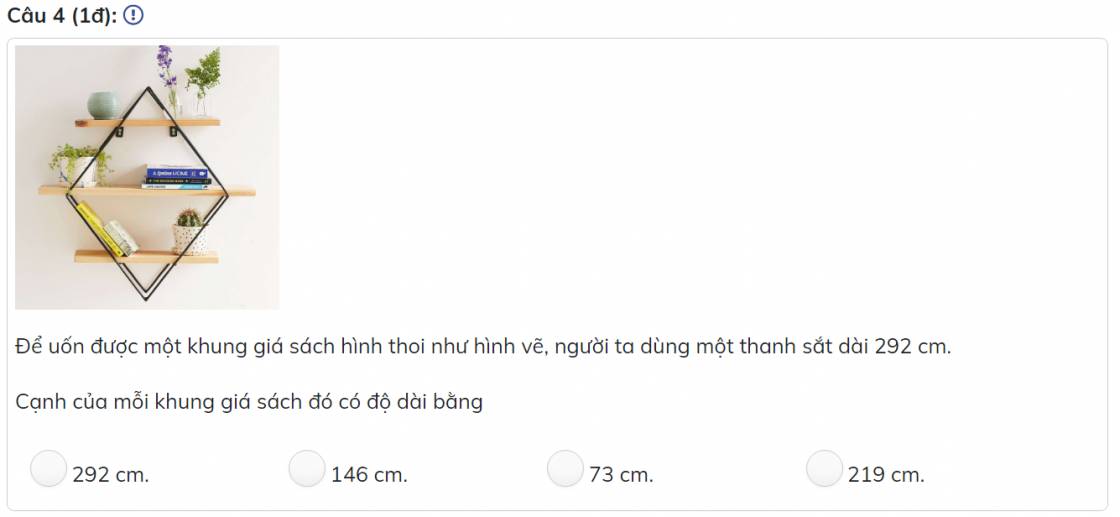
4 cạnh hình thoi bằng nhau nên;
Cạnh khung giá sách là:
\(292:4=73\left(cm\right)\)
Vậy chọn đáp án số 3

2021.2023
= (2020+1).(2022+1)
=2020.2022 +(2020+2022+1)
mà (2020+2022+1) >1
⇒ 2021.2023 > 2022.2020

Vì tấm bìa được cắt hết => cạnh của hình vuông là ước chung của chiều dài và chiều rộng hình chữ nhật.
Khi đó độ dài cạnh hình vuông lớn nhất chính là ƯCLN của chiều dài và chiều rộng hình chữ nhật.
Ta có: 60 = 22.3.5
96 = 25.3
ƯCLN(60;96) = 22.3 = 12
Cạnh hình vuông là 12 cm
Diện tích tấm bìa hình chữ nhật là 96 x 60 = \(5760\left(cm^2\right)\)
Để cắt tấm bìa thành a mảnh nhỏ hình vuông bằng nhau sao cho tấm bìa được cắt hết và cạnh hình vuông có độ dài lớn nhất là b (cm) thì a phải là số nhỏ nhất sao cho \(5760:a=b^2\)
Mà \(5760=2^7.3^2.5=\left(2^6.3^2\right).\left(2.5\right)\)
\(=\left(8^2.3^2\right).10=24^2.10\)
Nên khi số mảnh lớn nhất là a = 10 thì cạnh hình vuông có độ dài lớn nhất là 24 cm
\(5760=24^2.10\)
\(5760=24^2.10\)

BCNN(2;3;4;5;6)=60
B(60)={0;60;120;180;240;300;360;420...}
Vì số học sinh không quá 400 và thừa 1 khi xếp hàng
Nên số học sinh là {61;121;181;241;301;361}
Bội chung nhỏ nhất các số là:
\(2^2\cdot3\cdot5=60\)
Số học sinh là:
\(60+1=61\left(hs\right)\)
Đáp số: 61 học sinh

`@` `\text {Ans}`
`\downarrow`
\(\left(2\cdot x+2\right)^2=64\)
`\Rightarrow`\(\left(2x+2\right)^2=\left(\pm8\right)^2\)
`\Rightarrow`\(\left[{}\begin{matrix}2x+2=8\\2x+2=-8\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}2x=8+2\\2x=-8+2\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}2x=10\\2x=-6\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}x=10\div2\\x=-6\div2\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)
Vậy, `x \in {5; -3}`
`@` `\text {Kaizuu lv uuu}`

\(\dfrac{2\times x-4,36}{0,125}=0,25\times42,9-11,7\times0,25+0,25\times0,8\)
\(\dfrac{2\times x-4,36}{0,125}=0,25\times\left(42,9-11,7+0,8\right)\)
\(\dfrac{2\times x-4,36}{0,125}=0,25\times32=8\)
\(2\times x-4,36=8\times0,125=1\)
\(2\times x=1+4,36=5,36\)
\(x=5,36\div2\)
\(x=2,68\)