giúp e vvs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2 tháng 5 2024
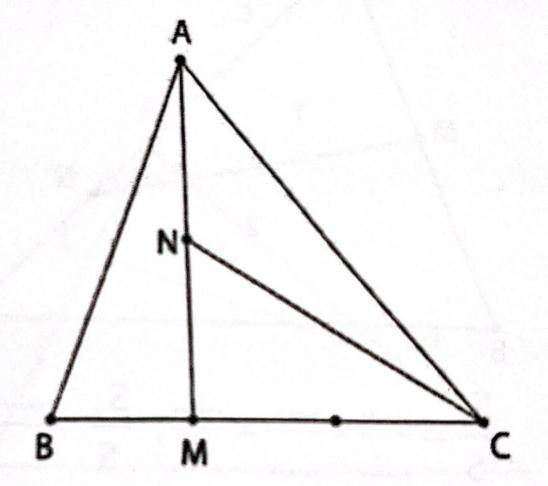
\(BM=\dfrac{1}{2}MC\)
=>\(\dfrac{CM}{CB}=\dfrac{2}{3}\)
=>\(S_{AMC}=\dfrac{2}{3}\times S_{ABC}=\dfrac{2}{3}\times48=32\left(cm^2\right)\)
Vì NA=NM
nên N là trung điểm của AM
=>\(AN=\dfrac{1}{2}MA\)
=>\(S_{ACN}=\dfrac{1}{2}\times S_{AMC}=\dfrac{1}{2}\times32=16\left(cm^2\right)\)
2 tháng 5 2024
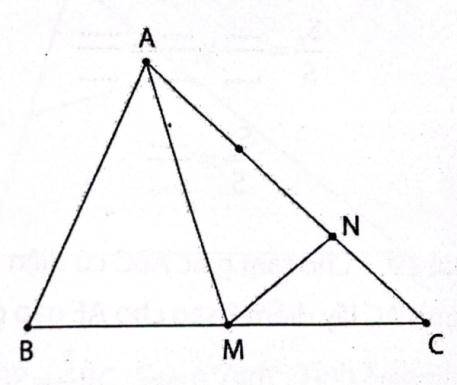
CN=1/3CA
=>\(S_{CMN}=\dfrac{1}{3}\times S_{AMC}\)
=>\(S_{AMC}=3\times4=12\left(cm^2\right)\)
Vì BM=MC
nên \(CM=\dfrac{1}{2}CB\)
=>\(S_{AMC}=\dfrac{1}{2}\times S_{ABC}\)
=>\(S_{ABC}=S_{AMC}\times2=12\times2=24\left(cm^2\right)\)
PC
1 tháng 5 2024
giúp mình bài này với mai cô kiểm tra rồi mà không biết cách làm. đoạn trung bình kia là sao mình chưa hiểu lắm
1 tháng 5 2024
Bạn tính chiều rộng thửa ruộng rồi tính dt thửa ruộng chia cho 100m2 là bằng kết quả
VG
1
2 tháng 5 2024
\(\dfrac{25-x}{56}=\dfrac{6}{16}\)
=>\(\dfrac{25-x}{56}=\dfrac{3}{8}\)
=>\(25-x=\dfrac{3}{8}\times56=21\)
=>x=25-21=4
2 tháng 5 2024
Khi x=-1;y=-1;z=-1 thì \(N=\left(-1\right)^1\cdot\left(-1\right)^2\cdot\left(-1\right)^3+\left(-1\right)^2\cdot\left(-1\right)^3\cdot\left(-1\right)^4+...+\left(-1\right)^{2014}\cdot\left(-1\right)^{2015}\cdot\left(-1\right)^{2016}\)
=1-1+1-1+...+1-1
=0