A = \(\dfrac{1}{10}\) + \(\dfrac{1}{15}\) + \(\dfrac{1}{21}\) + ... + \(\dfrac{1}{120}\)

A = \(\dfrac{2}{2}\).(\(\dfrac{1}{10}\) + \(\dfrac{1}{15}\) + \(\dfrac{1}{21}\) + ... + \(\dfrac{1}{120}\))

A = \(2\).(\(\dfrac{1}{20}\) + \(\dfrac{1}{30}\) + \(\dfrac{1}{42}\)... + \(\dfrac{1}{240}\))

A = 2.(\(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + ... + \(\dfrac{1}{15.16}\))

A = 2.(\(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\) + ... + \(\dfrac{1}{15}\) - \(\dfrac{1}{16}\))

A = 2.(\(\dfrac{1}{4}\) - \(\dfrac{1}{16}\))

A = 2.\(\dfrac{3}{16}\)

A = \(\dfrac{3}{8}\) 

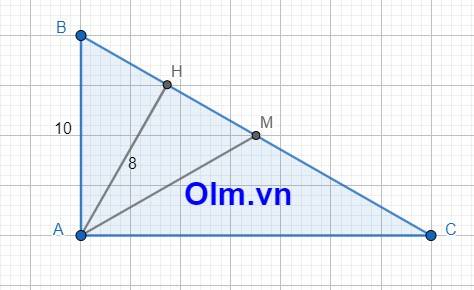
        Bài 1:

Theo pytago ta có: HB² + AH² = AB² 

          ⇒ HB² = AB² - AH² 

              HB² = 10² -  8² = 36 

              HB = \(\sqrt{36}\) = 6 (cm)

Xét tam giác ABC  và tam giác HBA có:

            \(\widehat{BAC}\) = \(\widehat{BHA}\) = 90⁰

            \(\widehat{ABC}\) = \(\widehat{HBA}\)

⇒ \(\Delta\) ABC \(\sim\) \(\Delta\) HBA (g - g)

⇒ \(\dfrac{AB}{HB}\) = \(\dfrac{BC}{BA}\)

      BC = \(\dfrac{AB}{HB}\) \(\times\) AB 

      BC = \(\dfrac{10.10}{6}\) = \(\dfrac{50}{3}\) (cm)

      S_ABC = \(\dfrac{1}{2}\)BC \(\times\)  AH  = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{50}{3}\) \(\times\) 8 = \(\dfrac{200}{3}\) (cm²)

Vì M là trung điểm của tam giác ABC nên 

   S_ABM  = \(\dfrac{1}{2}\) S_ABC (hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BM = \(\dfrac{1}{2}\) BC)

   S_ABM = \(\dfrac{200}{3}\).\(\dfrac{1}{2}\) = \(\dfrac{100}{3}\) (cm²)

  S_AHB = \(\dfrac{1}{2}\)AH.HB = \(\dfrac{8.6}{2}\) = 24 (cm²)

S_AHB + S_AHM = S_ABM

 ⇒ S_AHM = S_ABM - S_AHB 

    S_AHM = \(\dfrac{100}{3}\) - 24 = \(\dfrac{28}{3}\) (cm²)

Kết luận: BC dài \(\dfrac{50}{3}\) cm; Diện tích tam giác AHM là \(\dfrac{28}{3}\) cm²

P = (1 - 1/2024) × (1 - 1/2023) × (1 - 1/2022) × (1 - 1/2021)

= 2023/2024 × 2022/2023 × 2021/2022 × 2020/2021

= 2020/2024

= 505/506

               Bài 1:

Theo pytago ta có: HB² + AH² = AB² 

          ⇒ HB² = AB² - AH² 

              HB² = 10² -  8² = 36 

              HB = \(\sqrt{36}\) = 6 (cm)

Xét tam giác ABC  và tam giác HBA có:

            \(\widehat{BAC}\) = \(\widehat{BHA}\) = 90⁰

            \(\widehat{ABC}\) = \(\widehat{HBA}\)

⇒ \(\Delta\) ABC \(\sim\) \(\Delta\) HBA (g - g)

⇒ \(\dfrac{AB}{HB}\) = \(\dfrac{BC}{BA}\)

      BC = \(\dfrac{AB}{HB}\) \(\times\) AB 

      BC = \(\dfrac{10.10}{6}\) = \(\dfrac{50}{3}\) (cm)

      S_ABC = \(\dfrac{1}{2}\)BC \(\times\)  AH  = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{50}{3}\) \(\times\) 8 = \(\dfrac{200}{3}\) (cm²)

Vì M là trung điểm của tam giác ABC nên 

   S_ABM  = \(\dfrac{1}{2}\) S_ABC (hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BM = \(\dfrac{1}{2}\) BC)

   S_ABM = \(\dfrac{200}{3}\).\(\dfrac{1}{2}\) = \(\dfrac{100}{3}\) (cm²)

  S_AHB = \(\dfrac{1}{2}\)AH.HB = \(\dfrac{8.6}{2}\) = 24 (cm²)

S_AHB + S_AHM = S_ABM

 ⇒ S_AHM = S_ABM - S_AHB 

    S_AHM = \(\dfrac{100}{3}\) - 24 = \(\dfrac{28}{3}\) (cm²)

Kết luận: BC dài \(\dfrac{50}{3}\) cm; Diện tích tam giác AHM là \(\dfrac{28}{3}\) cm²

\(\dfrac{-3}{8}\cdot16\cdot\dfrac{8}{17}-0,375\cdot7\cdot\dfrac{9}{17}\)

\(=-\dfrac{3}{8}\cdot\dfrac{128}{17}-\dfrac{3}{8}\cdot\dfrac{63}{17}\)

\(=-\dfrac{3}{8}\left(\dfrac{128}{17}+\dfrac{63}{17}\right)=-\dfrac{3}{8}\cdot\dfrac{191}{17}=\dfrac{-573}{136}\)

- \(\dfrac{3}{8}\).16.\(\dfrac{8}{17}\) - 0,375.7\(\dfrac{9}{17}\)

Đề như này phải không em?

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có

BC chung

\(\widehat{EBC}=\widehat{DCB}\)(ΔABC cân tại A)

Do đó: ΔEBC=ΔDCB

b: ΔEBC=ΔDCB

=>\(\widehat{ECB}=\widehat{DBC}\)

=>\(\widehat{HBC}=\widehat{HCB}\)

=>ΔHBC cân tại H

ta có: HB=HC

=>H nằm trên đường trung trực của BC(1)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra AH là đường trung trực của BC

vẽ hình ra hộ cái

a: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-52^0}{2}=\dfrac{128^0}{2}=64^0\)

Xét ΔABC có \(\widehat{ACB}>\widehat{BAC}\)

mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC

nên AB>BC

b: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

Bài 8:

\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}\)

\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)

\(=\dfrac{1}{3}-\dfrac{1}{99}=\dfrac{33}{99}-\dfrac{1}{99}=\dfrac{32}{99}\)

Bài 6:

a: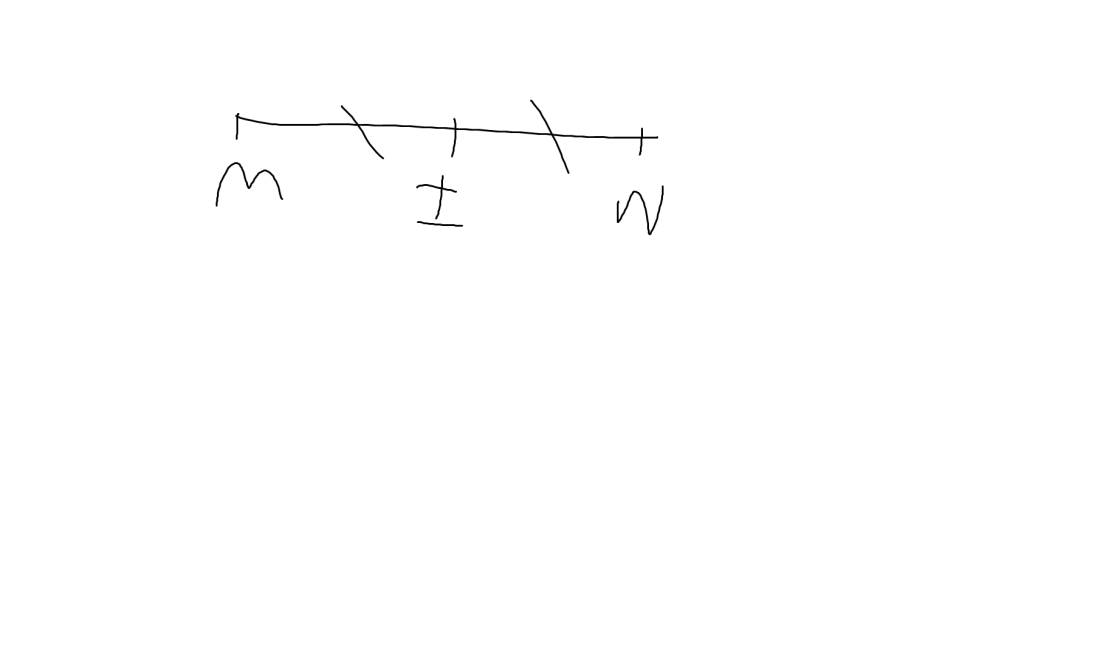 

b: I là trung điểm của MN

=>\(MI=\dfrac{MN}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)