\(F=\left|x+1\right|+\left|x-5\right|+\left|x+3\right|\)

\(=\left|x+1\right|+\left|5-x\right|+\left|x+3\right|\)

\(\ge\left|x+1\right|+\left|5-x+x+3\right|\)

\(=\left|x+1\right|+8\ge8\)

Dấu \(=\)khi \(\hept{\begin{cases}\left(5-x\right)\left(x+3\right)\ge0\\x+1=0\end{cases}}\Leftrightarrow x=-1\).

Biết làm rồi :>>>>>>

Ta có : D = 3 . | 2x - 1 | + | 6x - 4 |

=> D = | 3 | . | 2x - 1 | + | 6x - 4 |

=> D = | 6x - 3 | + | 6x - 4 |

Vì \(\hept{\begin{cases}\left|6x-3\right|\ge6x-3\forall x\\\left|6x-4\right|\ge-6x+4\forall x\end{cases}}\)

=> | 6x - 3 | + | 6x - 4 | ≥ ( 6x - 3 ) + ( -6x + 4 )

=> D ≥ 1

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}6x-3\ge0\\6x-4\le0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}6x\ge3\\6x\le4\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge\frac{1}{2}\\x\le\frac{2}{3}\end{cases}}\Leftrightarrow\frac{1}{2}\le x\le\frac{2}{3}\)

Tặng Hoàng Sơn một k

ớp 5 làm đc 

Gọi số cây trồng được của lớp 7A, 7B lần lượt là x (cây); y (cây).

Tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 nghĩa là x : y =0,8 hay

 .

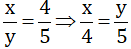
Lớp 7B trồng nhiều hơn lớp 7A là 20 cây nghĩa là y – x = 20.

Theo tính chất dãy tỉ số bằng nhau

Vậy Lớp 7A trồng được 80 cây

Lớp 7B trồng được 100 cây

7A: ██ cây

7B: ██ cây

        [Lưu ý: Nếu không nhìn thấy đáp số thì là do mạng nha]

đây nhé chúc bạn học tốt

Ta có: 

a3+3a2+5=5ba3+3a2+5=5b

⇔a2(a+3)+5=5b⇔a2(a+3)+5=5b

⇔a2.5c+5=5b⇔a2.5c+5=5b

⇔a2.5c−1+1=5b−1⇔a2.5c−1+1=5b−1

b-1=0 hoặc c-1=0
nếu b-1=0 thì thay vào không thỏa mãn
Nếu c-1=0 thì c=1 a=2 và b=2

Đáp án là:-1.6384x10^20

Tổng trên có 10 số hạng nhóm 2 số vào một nhóm ta được:

A = (2+2²)+(2³+2⁴)+...+(2⁹+2¹⁰)

A = 2(1+2) + 2³(1+2)+...+2⁹(1+2)

A = 2.3+2³.3+...+2⁹.3

A = 3(2+2³+...+2⁹) chia hết cho 3

Vậy tổng A chia hét cho 3

I don't know

Bài 1 góc còn lại = 100 độ

Bài 2 góc đối đỉnh xMz= 80 độ

         Các góc còn lại =100 độ

Câu 6: Hai đường thẳng xx’, yy’ cắt nhau và trong các góc tạo thành có một góc bằng 900, thì

A. xx' là đường trung trực của yy'.

B. xx' // уу'.

C. yy' là đường trung trực của xx'.

D. xx' vuông góc yy".

◥ὦɧ◤ᕼᗩᖇᖇƳ亗

zô rep tin nhắn tui với 

Làm ơn

:>

Từ x2=y5x2=y5

=>2x4=y5=>2x4=y5

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x4=y5=2x−y4−5=3−1=−32x4=y5=2x−y4−5=3−1=−3 ( vì 2x - y = 3 )

Do đó: x2=3=>x=−3⋅2=−6x2=3=>x=−3⋅2=−6

y5=3=>y=−3⋅5=−15y5=3=>y=−3⋅5=−15

Vậy (x;y)∈{(−6;−15)}

Ta có : \(\frac{x}{y}=\frac{2}{5}\)

\(\Rightarrow\)\(\frac{x}{2}=\frac{y}{5}\)

Đặt \(\frac{x}{2}=\frac{y}{5}=k\)

\(\Rightarrow\hept{\begin{cases}x=2k\\y=5k\end{cases}}\)

Thay vào \(2x-y=3\)ta có :

\(2.2k-5k=3\)

\(4k-5k=3\)

\(-1k=3\)

\(k=-3\)

Thay vào ta có :

\(\Rightarrow\hept{\begin{cases}x=2.\left(-3\right)=-6\\y=5.\left(-3\right)=-15\end{cases}}\)