\(\dfrac{2}{5}=\dfrac{4}{10}>\dfrac{3}{10}\) 

Ta xếp: \(\dfrac{2}{5};\dfrac{3}{10}\) 

\(\dfrac{2}{5}=\dfrac{6}{15}>\dfrac{7}{15}\)

Ta xếp: \(\dfrac{7}{15};\dfrac{2}{5};\dfrac{3}{10}\) 

Mà: \(\dfrac{3}{10}>0>-\dfrac{3}{4}\)  

Ta xếp: \(\dfrac{7}{15};\dfrac{2}{5};\dfrac{3}{10};0\)

\(-\dfrac{3}{4}=\dfrac{-9}{12}\) 

\(-\dfrac{5}{6}=\dfrac{-10}{12}\)

\(\Rightarrow-\dfrac{3}{4}>\dfrac{-5}{6}\) (vì \(-\dfrac{9}{12}>\dfrac{-10}{12}\))

Ta xếp: \(\dfrac{7}{15};\dfrac{2}{5};\dfrac{3}{19};0;-\dfrac{3}{4};-\dfrac{5}{6}\)

\(\dfrac{-3}{4}=\dfrac{-9}{12}\); \(\dfrac{-5}{6}\) = \(\dfrac{-10}{12}\); \(\dfrac{3}{10}\) = \(\dfrac{9}{30}\); \(\dfrac{7}{15}\) = \(\dfrac{14}{30}\); \(\dfrac{2}{5}\) = \(\dfrac{12}{30}\)

\(\dfrac{-10}{12}\) < \(\dfrac{-9}{12}\) < 0 < \(\dfrac{9}{30}\)< \(\dfrac{12}{30}\)< \(\dfrac{14}{30}\)

Vậy các phân số đã cho được sắp xếp theo thứ tự giảm dần là:

\(\dfrac{7}{15}\); \(\dfrac{2}{5}\); \(\dfrac{3}{10}\); 0; \(\dfrac{-3}{4}\); \(\dfrac{-5}{6}\)

2569 35 73 119 14

54673 35 1562 196 217 73 3

\(A=\dfrac{10^{2012}+1}{10^{2011}+1}\)

Mà ta có: \(10^{2012}+1>10^{2011}+1\)

\(\Rightarrow A=\dfrac{10^{2022}+1}{10^{2011}+1}>1\) (1) 

\(B=\dfrac{10^{2011}+1}{20^{2010}+1}\)

Mà ta có: \(20^{2010}+1>10^{2011}+1\)

\(\Rightarrow B=\dfrac{10^{2011}+1}{20^{2010}+1}< 1\) (2)

Từ (1) và (2) \(\Rightarrow A>B\)

Bài 5

1) x ∈ Ư(18) = {1; 2; 3; 6; 9; 18}

x ∈ B(4) = {0; 4; 8; 12; 16; 20; ...}

Vậy không tìm được x thỏa mãn đề bài

2) x ∈ Ư(20) = {1; 2; 4; 5; 10; 20}

x ∈ B(2) = {0; 2; 4; 6; 8; 10; 12; 14; 16; 18; 20; ...}

⇒ x ∈ {2; 4; 10; 20}

3) x ∈ B(12) = {0; 12; 24; 36; 48; ...; 96; 108; ...}

Mà 30 ≤ x ≤ 100

⇒ x ∈ {36; 48; ...; 96}

4) x ∈ Ư(150) = {1; 2; 3; 5; 6; 10; 15; 25; 30; 50; 75; 150}

Mà x ≤ 50

⇒ x ∈ {1; 2; 3; 5; 6; 10; 15; 25; 30; 50}

5) 70 ⋮ x và 168 ⋮ x

⇒ x ∈ ƯC(70; 168)

Ta có:

70 = 2.5.7

168 = 2³.3.7

⇒ ƯCLN(70; 168) = 2.7 = 14

⇒ x ∈ ƯC(70; 168) = Ư(14) = {1; 2; 7; 14}

Mà x > 10

⇒ x = 14

6) Ta có:

(1995 + 2005 + x) ⋮ 5

1995 ⋮ 5

2005 ⋮ 5

⇒ x ⋮ 5

⇒ x ∈ B(5) = {0; 5; 10; 15; 20; 25; 30; 35; 40; ...}

Mà 23 < x ≤ 35

⇒ x ∈ {25; 30; 35}

Bài 6

1) Do 17x2y chia hết cho 2 và 5 nên y = 0

⇒ Số đã cho có dạng: 17x20

Để 17x20 chia hết cho 3 thì (1 + 7 + x + 2 + 0) ⋮ 3

⇒ (10 + x) ⋮  3

⇒ x ∈ {2; 5; 8}

Vậy x ∈ {2; 5; 8}; y = 0

2) Do 234xy chia hết cho 2 và 5 nên y = 0

⇒ Số đã cho có dạng: 234x0

Để 234x0 chia hết cho 9 thì (2 + 3 + 4 + x + 0) ⋮ 9

⇒ (9 + x) ⋮ 9

⇒ x ∈ {0; 9}

Vậy x ∈ {0; 9}; y = 0

3) Do 4x6y chia hết cho 2 và 5 nên y = 0

Mà x - y = 4

⇒ x = 4 + y

⇒ x = 4

Vậy x = 4; y = 0

4) Do 57x2y chia hết cho 5 nhưng không chia hết cho 2 nên y = 5

⇒ Số đã cho có dạng 57x25

Để 57x25 chia hết cho 9 thì (5 + 7 + x + 2 + 5) ⋮ 9

⇒ (19 + x) ⋮ 9

⇒ x = 8

Vậy x = 8; y = 5

Đúng rồi em nhé.

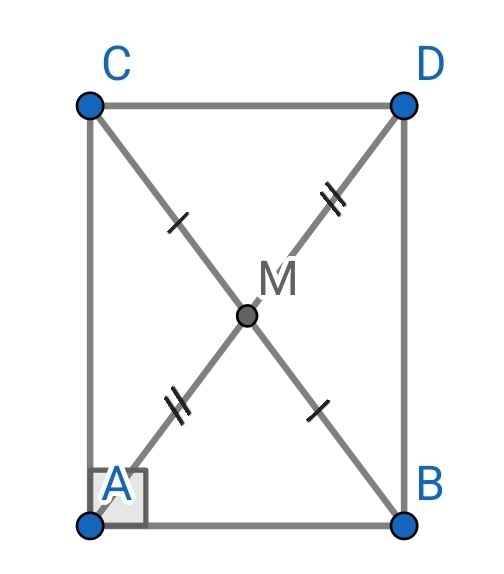 a) Do M là trung điểm của BC (gt)

⇒ MB = MC

Xét ∆MAB và ∆MDC có:

MA = MD (gt)

∠AMB = ∠DMC (đối đỉnh)

MB = MC (cmt)

⇒ ∆MAB = ∆MDC (c-g-c)

b) Do ∆MAB = ∆MDC (cmt)

⇒ ∠MAB = ∠MDC (hai góc tương ứng)

Mà ∠MAB và ∠MDC là hai góc so le trong

⇒ AB // CD

c) Do MA = MD (gt)

⇒ AD = 2AM

Do ∆ABC vuông tại A (gt)

⇒ AB ⊥ AC

Mà AB // CD (cmt)

⇒ CD ⊥ AC

⇒ ∆CDA vuông tại C

Do ∆MAB = ∆MDC (cmt)

⇒ AB = CD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆ABC và ∆CDA có:

AC là cạnh chung

AB = CD (cmt)

⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)

⇒ BC = AD (hai cạnh tương ứng)

Mà AD = 2AM (cmt)

⇒ BC = 2AM

d) Xét ∆MAC và ∆MDB có:

MA = MD (gt)

∠AMC = ∠DMB (đối đỉnh)

MC = MB (cmt)

⇒ ∆MAC = ∆MDB (c-g-c)

⇒ ∠MAC = ∠MDB (hai góc tương ứng)

Mà ∠MAC và ∠MDB là hai góc so le trong

⇒ AC // BD

Mà AC ⊥ AB (cmt)

⇒ AB ⊥ BD

5x+5x+1+5x+2=31

5x + 5x + 5x = 31 - 2 - 1 

15x = 28

x= 28/15

Bài 1:

Xét 3 điểm không thẳng hàng ta có:

Cứ 1 điểm tạo với 3 -  1 điểm còn lại  3 - 1 đường thẳng.

Với 3 điểm sẽ tạo được số đường thẳng là: (3- 1) x 3 đường thẳng

Theo cách tính trên mỗi đường thẳng được tính hai lần

Vậy thực tế số đường thẳng là: (3 - 1) x 3 : 2  = 3 (đường thẳng)

Số điểm thẳng hàng là: 20 - 3  = 17 (điểm)

Vì 17 điểm này thẳng hàng với nhau nên qua 17 điểm này ta chỉ kẻ được một đường thẳng duy nhất là đường thẳng d

Xét 3 điểm nằm ngoài đường thẳng d với 17 điểm nằm trên đường thẳng d ta có:

Cứ 1 điểm nằm ngoài đường thẳng d ta có thể kẻ được với 17 điểm nằm trên đường thẳng d số đường thẳng là 17 đường thẳng.

Với 3 điểm nằm ngoài đường thẳng d ta có thể kẻ được với 17 điểm trên đường thẳng d số đường thẳng là: 

 17 x 3  = 51 (đường thẳng)

Từ các lập luận trên ta có Tất cả số đường thẳng tạo được là:

       3 + 1 + 51 = 55 (đường thẳng)

Đs..

Bài 2:

+ Xét số điểm không thẳng hàng

Số điểm không thẳng hàng là: 

      20 -  5  = 15 (điểm)

Cứ 1 điểm sẽ tạo với 15 - 1 điểm còn lại 15 - 1 đường thẳng

Với 15 điểm ta sẽ tạo được số đường thẳng là: (15 - 1) x 15 đường thẳng.

Theo cách tính trên mỗi đường thẳng sẽ được tính hai lần. Vậy thực tế số đường thẳng là:

             (15  - 1) x 15 : 2  =  105 (đường thẳng)

Xét 5 điểm thẳng hàng, vì 5 điểm này thẳng hàng với nhau nên qua 5 điểm đó ta chỉ kẻ được duy nhất một đường thẳng là đường thẳng d.

Xét  15 điểm nằm ngoài đường thẳng d với 5 điểm nằm trên đường thẳng d ta có:

Cú 1 điểm nằm ngoài đường thẳng d tạo với 5 điểm nằm trên đường thẳng d số đường thẳng là 5 đường thẳng.

Với 15 điểm nằm ngoài đường thẳng d sẽ tạo được với 5 điểm trên đường thẳng d số đường thẳng là: 

5 x 15  =  75 (đường thẳng)

Từ những lập luận trên ta có số đường thẳng được tạo sẽ là:

  105 + 1 + 75 = 181  (đường thẳng)

đs...

Gọi chữ số cần lập có dạng �����‾abcde

- Nếu các chữ số không yêu cầu đôi một khác nhau:

$e$ có 4 cách chọn, $a$ có 6 cách chọn; 3 vị trí còn lại đều có 7 cách chọn

$\Rightarrow$ có $\mathrm{4.6.7.7.7}=8232$ số

- Nếu các chữ số đôi một khác nhau:

+ Nếu $e=0$: $a$ có 6 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn $\Rightarrow$ có $\mathrm{6.5.4.3}=360$ số

+ Nếu $e\ne 0\Rightarrow e$ có 3 cách chọn, a có 5 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn $\Rightarrow 900$ số

$\Rightarrow$ có $900+360=1260$ số

Lời giải:

Gọi số tự nhiên có 5 chữ số khác nhau là $\overline{abcde}$

Số cách lập số tự nhiên có 5 chữ số khác nhau từ 2,3,4,5,6 là: $5!=120$ số

Số cách lập số tự nhiên có 5 chữ số khác nhau từ 2,3,4,5,6 mà chia hết cho 5 là:

$4!.1=24$ số (do e chỉ có 1 cách chọn là số 5, 4 số còn lại hoán vị là 4!)

Số cách lập số tự nhiên có 5 chữ số khác nhau mà không chia hết cho 5:

$120-24=96$ (số)