Cho \(S=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}...\dfrac{4046}{4047}\). Chứng minh rằng \(S^2< \dfrac{1}{2024}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
b: M nằm giữa O và N
=>MO+MN=ON
=>MN+2=4
=>NM=2(cm)
ta có: M nằm giữa O và N
mà MO=MN(=2cm)
nên M là trung điểm của ON

\(300=2^2\cdot5^2\cdot3;276=2^2\cdot3\cdot24;252=2^2\cdot3^2\cdot7\)
=>\(ƯCLN\left(300;276;252\right)=2^2\cdot3=12\)
=>Có thể xếp được tối đa là 12 hàng dọc để không ai bị lẻ hàng
Khối 6 sẽ có 300:12=25 hàng ngang
Khối 7 sẽ có 276:12=23 hàng ngang
Khối 8 sẽ có 252:12=21 hàng ngang

Gọi d=ƯCLN(7n+4;5n+3)
=>\(\left\{{}\begin{matrix}7n+4⋮d\\5n+3⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}35n+20⋮d\\35n+21⋮d\end{matrix}\right.\)
=>\(35n+21-35n-20⋮d\)
=>\(1⋮d\)
=>d=1
=>ƯCLN(7n+4;5n+3)=1
=>\(\dfrac{7n+4}{5n+3}\) là phân số tối giản


a: Các tia đối nhau gốc O là:
Ox;Oy
OA;Oy
OB;Ox
OA;OB
b: Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>OA+OB=BA
=>OB+3=6
=>OB=3(cm)
Ta có: O nằm giữa A và B
mà OA=OB(=3cm)
nên O là trung điểm của AB
c: 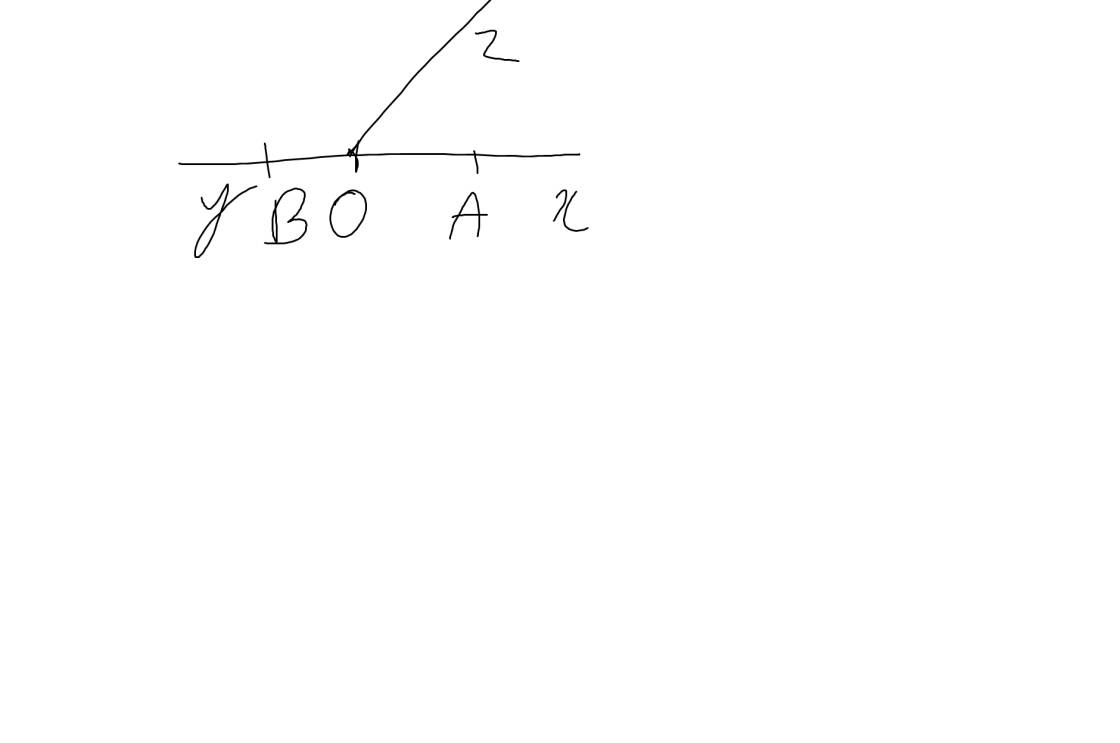

\(\dfrac{-5}{8}\times\dfrac{-12}{29}\times\dfrac{8}{-10}\times5,8\)
\(=-\dfrac{5}{8}\times\dfrac{8}{10}\times5,8\times\dfrac{12}{29}\)
\(=-\dfrac{5}{10}\times\dfrac{29}{5}\times\dfrac{12}{29}\)
\(=-\dfrac{5}{10}\times\dfrac{12}{5}=-\dfrac{12}{10}=-\dfrac{6}{5}\)

a: Các tia đối nhau gốc O là:
Ox;Oy
OA;Oy
OB;Ox
OA;OB
b: Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>OA+OB=BA
=>OB+3=6
=>OB=3(cm)
Ta có: O nằm giữa A và B
mà OA=OB(=3cm)
nên O là trung điểm của AB
c: 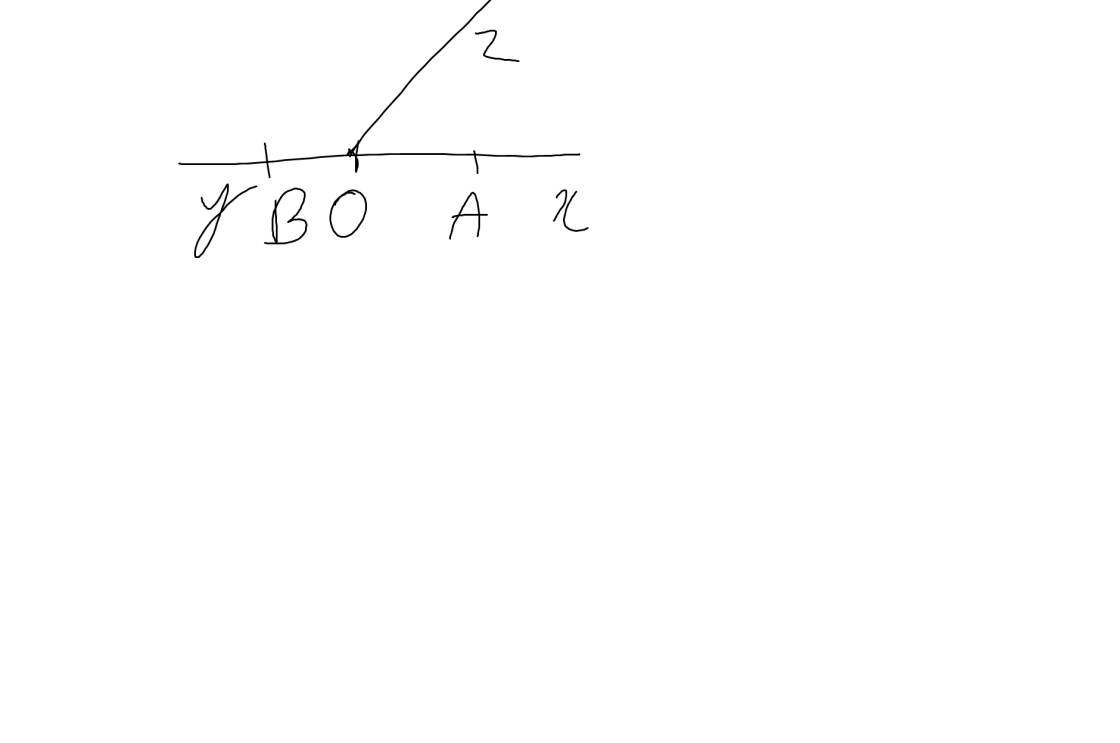

Lời giải:
$S^2=\frac{(2.4.6...4046)^2}{(3.5.7...4047)^2}$
$=\frac{2.4}{3^2}.\frac{4.6}{5^2}.\frac{6.8}{7^2}.....\frac{4044.4046}{4045^2}.\frac{2.4046}{4047^2}$
Xét thừa số tổng quát $\frac{n(n+2)}{(n+1)^2}=\frac{n^2+2n}{n^2+2n+1}< 1$
$\Rightarrow \frac{2.4}{3^2}< 1; \frac{4.6}{5^2}<1,...., \frac{4044.4046}{4045^2}<1$
$\Rightarrow S^2< 1.\frac{2.4046}{4047^2}$
Giờ chỉ cần cm: $\frac{2.4046}{4047^2}< \frac{1}{2024}$
Thật vậy:
$\frac{2.4046}{4047^2}-\frac{1}{2024}=\frac{4048.4046-4047^2}{2024.4047^2}=\frac{(4047+1)(4047-1)-4047^2}{2024.4047^2}=\frac{4047^2-1-4047^2}{2024.4047^2}=\frac{-1}{2024.4047^2}< 0$
$\Rightarrow \frac{2.4046}{4047^2}< \frac{1}{2024}$
$\Rightarrow S^2< \frac{1}{2024}$