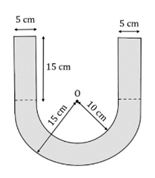
1) (0,5 điểm) Vẽ đồ thị hàm số $y=-\dfrac14x^2$.
2) (1,5 điểm) Cho phương trình $x^2-2mx+m^2-1=0$ (m là tham số) (1)
a) Giải phương trình (1) khi $m=-3$.
b) Tìm $m$ để phương trình (1) có hai nghiệm phân biệt $x_1; \, x_2$ thỏa mãn hệ thức: $(1+x_1)(2-x_2)+(1+x_2)(2-x_1)=x_{1}^{2}+x_{2}^{2}-x_1x_2-2$.

bài 2: a) thay m = -3 vào (1) ta được:
\(x^2-2\cdot\left(-3\right)x+\left(-3\right)^2-1=0\\ x^2+6x+9-1=0\\ x^2+6x+8=0\\ =>\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\)
b. từ (1) theo vi-et ta có; \(x_1+x_2=2m;x_1x_2=m^2-1\)
\(\left(1+x_1\right)\left(2-x_2\right)+\left(1+x_2\right)\left(2-x_1\right)=x_1^2+x_2^2-x_1x_2-2\\ \left(2-x_2+2x_1-x_1x_2\right)+\left(2-x_1+2x_2-x_1x_2\right)=x_1^2+x_2^2-x_1x_2-2\\ 2-x_2+2x_1-x_1x_2+2-x_1+2x_2-x_1x_2=x_1^2+x_2^2-x_1x_2-2\\ 4+x_1+x_2-2x_1x_2=x_1^2+x_2^2-x_1x_2-2\\ 6+2m-2m^2=m^2+1\\ 6+2m-2m^2-m^2-1=0\\ -3m^2+2m+5=0\\ 3m^2-2x-5=0\\ =>\left[{}\begin{matrix}m=\dfrac{5}{3}\\m=-1\end{matrix}\right.\)
vậy m = 5/3 hoặc m = -1