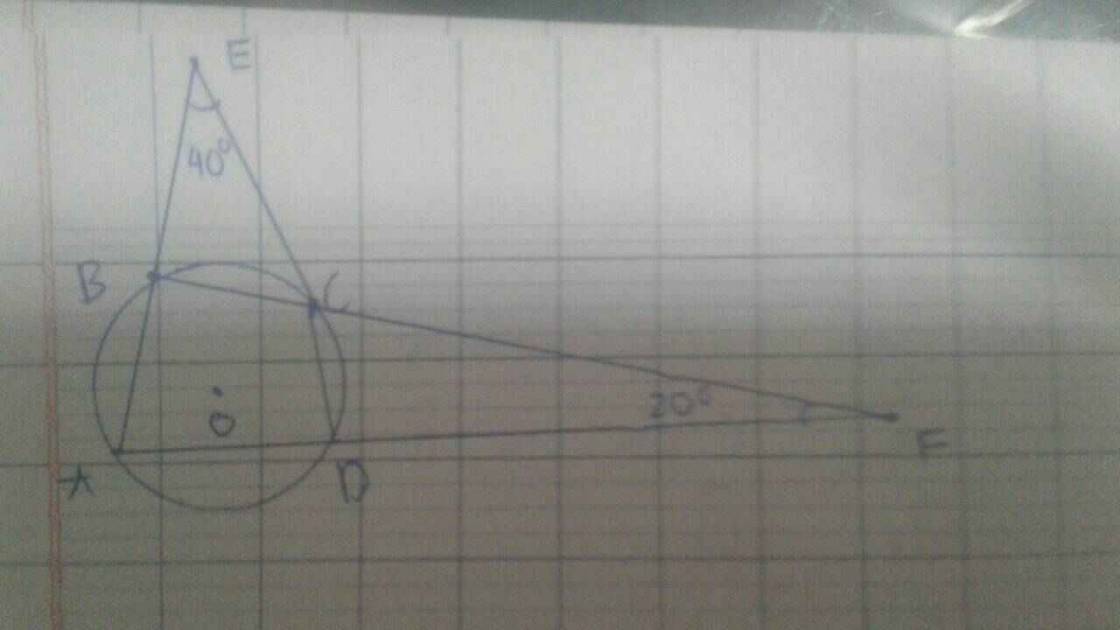
Tìm góc A,B,C,D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Gọi độ dài cạnh góc vuông thứ nhất và hai lần lượt là $a,b$ (m)
Theo bài ra ta có:
$ab=20.2=40$
$\sqrt{(a+2)^2+(b+5)^2}=\sqrt{a^2+b^2}+100$
$\Rightarrow (a+2)^2+(b+5)^2=a^2+b^2+10000+200\sqrt{a^2+b^2}$
$\Rightarrow 4a+10b=10^4-29+200\sqrt{a^2+b^2}$ (điều này là vô lý)
Đề có vẻ không đúng. Bạn xem lại

ĐKXĐ: \(xy\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+\dfrac{1}{y}\right)^2+x+\dfrac{1}{y}-\dfrac{2x}{y}=4\\\left(x+\dfrac{1}{y}\right)^2+\dfrac{x}{y}\left(x+\dfrac{1}{y}\right)-\dfrac{2x}{y}=4\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x+\dfrac{1}{y}=u\\\dfrac{x}{y}=v\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u^2+u-2v=4\\u^2+uv-2v=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u^2+u-2v=4\\u\left(v-1\right)=0\end{matrix}\right.\)
TH1: \(u=0\) thế vào \(u^2+u-2v=4\Rightarrow v=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x+\dfrac{1}{y}=0\\\dfrac{x}{y}=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\pm\sqrt{2}\\y=\mp\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
TH2: \(v=1\) thế vào \(u^2+u-2v=4\Rightarrow u^2+u-6=0\Rightarrow\left[{}\begin{matrix}u=2\\u=-3\end{matrix}\right.\)
TH2.1: \(\left\{{}\begin{matrix}x+\dfrac{1}{y}=2\\\dfrac{x}{y}=1\end{matrix}\right.\) tự giải
TH2.2: \(\left\{{}\begin{matrix}x+\dfrac{1}{y}=-3\\\dfrac{x}{y}=1\end{matrix}\right.\) tự giải

Đề bài sai, ví dụ \(a=1;b=-\dfrac{5}{2};c=2\) thỏa mãn \(\dfrac{a}{6}+\dfrac{b}{5}+\dfrac{c}{6}=0\) nhưng phương trình \(x^2-\dfrac{5}{2}x+2=0\) vô nghiệm


\(\sqrt[3]{x}-20+\sqrt{x}+15=7\)
\(\sqrt[3]{x}-20+15+\sqrt{x}=7\)
\(\sqrt[3]{x}-5+\sqrt{x}=7\)
\(\sqrt[3]{x}+\sqrt{x}=7+5\)
\(\sqrt[3]{x}+\sqrt{x}=12\)
còn lại mình chịu
\(\sqrt[3]{x}+\sqrt{x}=12=8+4\)
\(\sqrt[3]{x}=8\) và \(\sqrt{x}=4\)
Vậy x = 2


a, Gọi I là trung điểm của BC
Tam giác BEC vuông tại E trung tuyến EI nên IE = IB = IC
Tam giác BFC vuông tại F trung tuyến FI nên IF = IB = IC
Vậy tứ giác BEFC cùng thuộc đường tròn tâm I bán kính IB
b, Ta có :
\(\widehat{ACK}=90^0\) ( góc nội tiếp chắn nửa đường tròn )
= > BH // CK ( cùng vuông góc với AC )
Tương tự ta cũng có CH // BK
= > BHCK là hình bình hành
= > 2 đường chéo cắt nhau tại trung điểm của mỗi đường
Mà I là trung điểm của BC
= > H,I,K thẳng hàng ( đpcm )
c, Dễ thấy các tứ giác AFHE và BFHD nội tiếp nên :
\(\widehat{DFE}=\widehat{DFH}+\widehat{HFE}=\widehat{HBD}+\widehat{HAF}=2\widehat{HBD}=2.\left(90^0-\widehat{C}\right)=180^0-2\widehat{C}\)
( Do góc HBD và HAF cùng phụ với góc C )
Lại có :
Tam giác EIC cân tại I nên :
\(\widehat{EIC}=180^0-\widehat{IEC}-\widehat{ECI}=180^0-2\widehat{C}\)
\(=>\widehat{EIC}=\widehat{DFE}\)
= > Tứ giác DFEI là tứ giác nội tiếp
= > D,F,E,I cùng thuộc 1 đường tròn

Gọi chiều dài hcn là x ( x > 0 )
Chiều rộng hcn là y ( y > 0)
Nửa chu vi hcn là: x + y = 200 : 2 = 100 cm
Chiều dài gấp 3 lần chiều rộng => x = 3y => x - 3y = 0
Ta có hệ phương trình
\(\left\{{}\begin{matrix}x-3y=0\\x+y=100\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=75\\y=25\end{matrix}\right.\)
Diện tích hcn là: 75 x 25 = 1875 cm vuông
Gọi chiều dài , chiều rộng của hình chữ nhật lần lượt là a,b ( a,b > 0 ) ( cm )
Theo đề bài ta có :
chiều dài gấp 3 lần chiều rộng hay a = 3b
Ta lại có : 2 ( a + b ) = 200
<=> a + b = 100
Thay a = 3b vào phương trình ta được
3b + b = 100
<=> 4b = 100 <=> b = 25 ( cm )
a = 25 . 3 = 75 ( cm )
Vậy chiều dài hình chữ nhật là 75 cm , chiều rộng là 25 cm

Hình bạn tự vẽ nhé
Ta có KB , KC là tiếp tuyến của (O)
= > \(KB\perp OB,OK\perp BC\)
Ta có \(KH\perp AO\) \(\Rightarrow\widehat{KHO}=\widehat{AMO}=90^0\left(KO\perp BC\right)\)
\(\Rightarrow\Delta OMA\sim\Delta OHK\left(g.g\right)\)
\(\Rightarrow\dfrac{OM}{OH}=\dfrac{OA}{OK}=>OM.OK=OH.OA\)
Mà \(KO\perp BC,OB\perp KB=>OB^2=OM.OK=> OH.OA=OB^2\)
\(=OE^2\left(OE=OB\right)\)
\(\Rightarrow\dfrac{OE}{OH}=\dfrac{OA}{OE}=>\Delta OEH\sim\Delta OAE\left(c.g.c\right)\)
\(=>\widehat{OEA}=\widehat{OHE}=90^0\) hay AE là tiếp tuyến của ( O )
Áp dụng định lý về tổng 3 góc trong tam giác và định lý tứ giác nội tiếp, ta có:
\(\left\{{}\begin{matrix}A+B=180^0-20^0\\A+D=180^0-40^0\\B+D=180^0\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A+B=160^0\\A+D=140^0\\B+D=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2A+B+D=300^0\\B+D=180^0\end{matrix}\right.\)
\(\Rightarrow2A+180^0=300^0\)
\(\Rightarrow A=60^0\)
\(\Rightarrow B=160^0-A=100^0\)
\(C=180^0-A=120^0\)
\(D=180^0-B=80^0\)