Bổ sung đề; MB\(\perp\)OB tại B

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có

OM chung

\(\widehat{AOM}=\widehat{BOM}\)(OM là phân giác của góc AOB)

Do đó: ΔOAM=ΔOBM

=>MA=MB

b: Ta có: ΔOAM=ΔOBM

=>OA=OB

=>ΔOAB cân tại O

c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có

MA=MB

\(\widehat{AMD}=\widehat{BME}\)(hai góc đối đỉnh)

Do đó: ΔMAD=ΔMBE

=>MD=ME

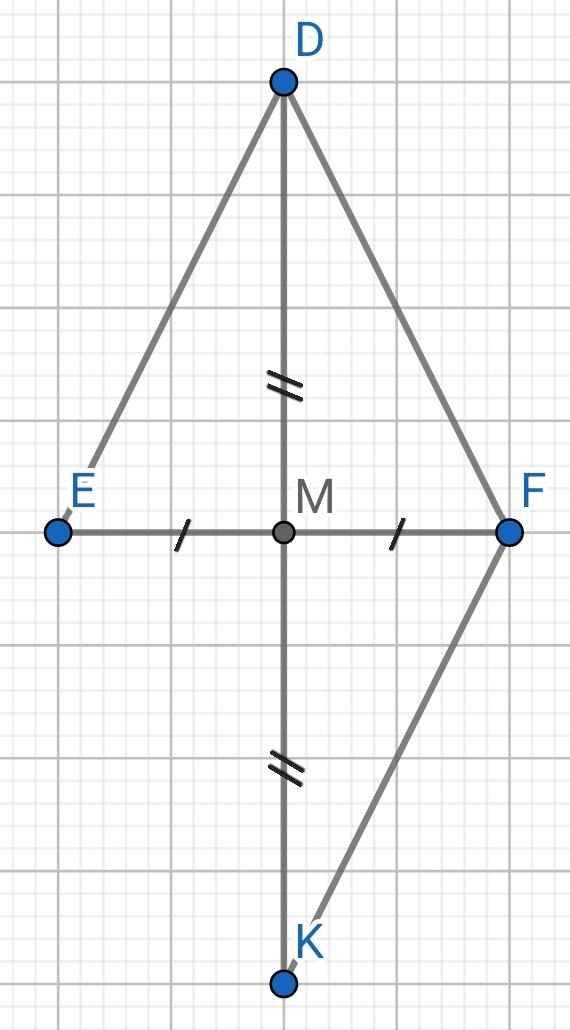
a) Do ∆DEF cân tại D (gt)

⇒ DE = DF

Do M là trung điểm của EF (gt)

⇒ ME = MF

Xét ∆DEM và ∆DFM có:

DE = DF (cmt)

DM là cạnh chung)

ME = MF (cmt)

⇒ ∆DEM = ∆DFM (c-c-c)

b) Sửa đề: Chứng minh DM ⊥ EF

Do ∆DEM = ∆DFM (cmt)

⇒ ∠DME = ∠DMF (hai góc tương ứng)

Mà ∠DME + ∠DMF = 180⁰ (kề bù)

⇒ ∠DME = ∠DMF = 180⁰ : 2 = 90⁰

⇒ DM ⊥ EF

c) Xét ∆DEM và ∆KFM có:

DM = KM (gt)

∠DME = ∠KMF (đối đỉnh)

ME = MF (cmt)

⇒ ∆DEM = ∆KFM (c-g-c)

⇒ DE = KF (hai cạnh tương ứng)

Mà DE = DF (cmt)

⇒ KF = DF

⇒ ∆FDK cân tại F

a) Ta có :

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)

\(\Rightarrow k^3=\dfrac{x}{3}.\dfrac{y}{4}.\dfrac{z}{5}=\dfrac{480}{3.4.5}=8\)

\(\Rightarrow k=2\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=2\\\dfrac{y}{4}=2\\\dfrac{z}{5}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=8\\z=10\end{matrix}\right.\)

Vậy \(\left\{{}\begin{matrix}x=6\\y=8\\z=10\end{matrix}\right.\)

b) Ta có :

\(\dfrac{a}{4}=\dfrac{b}{8}=\dfrac{c}{16}\)

\(\Rightarrow\left(\dfrac{a}{4}\right)^2=\left(\dfrac{b}{8}\right)^2=\left(\dfrac{c}{16}\right)^2\)

\(\Rightarrow\dfrac{a^2}{16}=\dfrac{b^2}{64}=\dfrac{c^2}{256}\)

Áp dụng TCDTSBN, ta có :

\(\dfrac{a^2}{16}=\dfrac{b^2}{64}=\dfrac{c^2}{256}=\dfrac{a^2-b^2}{16-64}=\dfrac{-60}{-48}=\dfrac{5}{4}\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a^2}{16}=\dfrac{5}{4}\\\dfrac{b^2}{64}=\dfrac{5}{4}\\\dfrac{c^2}{256}=\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2=4.5\\b^2=16.5\\c^2=256.5\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=\pm2\sqrt[]{5}\\b=\pm4\sqrt[]{5}\\c=\pm16\sqrt[]{5}\end{matrix}\right.\)

Vậy \(\left\{{}\begin{matrix}a=\pm2\sqrt[]{5}\\b=\pm4\sqrt[]{5}\\c=\pm16\sqrt[]{5}\end{matrix}\right.\)

a) Áp dụng TCDTSBN, ta có :

\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{4}=\dfrac{2x-4y+z}{1.2-4.2+4}=\dfrac{-6}{-2}=3\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{1}=3\\\dfrac{y}{2}=3\\\dfrac{z}{4}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=6\\z=12\end{matrix}\right.\)

Vậy \(\left\{{}\begin{matrix}x=3\\y=6\\z=12\end{matrix}\right.\)

b) Áp dụng TCDTSBN, ta có :

\(\dfrac{a}{2}=\dfrac{b}{-4}=\dfrac{c}{6}=\dfrac{a-5b+4c}{2-5.\left(-4\right)+4.6}=\dfrac{23}{46}=\dfrac{1}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=\dfrac{1}{2}\\\dfrac{b}{-4}=\dfrac{1}{2}\\\dfrac{c}{4}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=2\end{matrix}\right.\)

Vậy \(\left\{{}\begin{matrix}a=1\\b=-2\\c=2\end{matrix}\right.\)

A B C H K I M

a/

Xét tg vuông AHB và tg vuông AHC có

AB = AC (cạnh bên tg cân)

HB = HC (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)

=> tg AHB = tg AHC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)

b/

Xét tg ABC có

HB = HC (cmt); HK//AB (gt) => KA=KC (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)

Xét tg vuông AHC có

KA=KC (cmt)

\(\Rightarrow HK=KA=KC=\dfrac{AC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)

=> tg AHK cân tại K

c/

Xét tg vuông ABC có

HB=HC (cmt); KA=KC (cmt) => I là trọng tâm của tg ABC 

=> CI là trung uyến của tg ABC (trong tg 3 đường trung tuyến đồng quy) \(\Rightarrow M\in CI\) => C, I, M thẳng hàng

A B C M A'

Kéo dài AM cắt BC tại A'.

Xét ΔABA' ta có BĐT: AB + BA' > AA' = MA + MA'

                            hay AB + BA' > MA + MA'  (1)

Xét ΔCMA' ta có BĐT:    CA' > MC - MA' (2)  Cộng theo vế (1) và (2) ta được:

(AB + BA' ) + CA'  > ( MA + MA' ) + ( MC - MA' )  <===> AB + (BA' + CA') > MA + MC

Hay:  AB + CB > MA + MC  (I)  Chứng minh tương tự ta có:

         AB + AC > MB + MC  (II)

         CB + AC > MA + MB  (III) Cộng theo vế (I),(II) và (III) ta được:

2(AB+AC+CB) > 2(MA + MB + MC) 

Hay: MA+MB+MC < AB+AC+CB    (đpcm).

Số nguyên dương này không thể xác định vì số chữ số của số đó chưa xác định là bao nhiêu.

B=2.2/1.3 . 3.3/2.4 . 4.4/3.5 ......20.20/19.21

=2.3.4.....20/1.2.3.....19 . 2.3.4....20/3.4.5.....21

=20 . 2/21

=40/21

a: Quãng đường xe đạp đi được trong 2 giờ đầu tiên là:

2*20=40(km)

Quãng đường xe đạp đi được từ giớ thứ 3 đến lúc gặp ô tô là:

20(x-2)(km)

Độ dài quãng đường xe đạp đi được cho đến lúc gặp ô tô là:

20(x-2)+40=20x(km)

b: Độ dài quãng đường ô tô đi được cho đến lúc gặp xe đạp là:

60(x-2)(km)

c: Theo đề, ta có:

20x=60(x-2)

=>60x-120=20x

=>40x=120

=>x=3

a: \(H\left(x\right)+P\left(x\right)=x^5-2x^2+2\)

=>\(P\left(x\right)=x^5-2x^2+2-H\left(x\right)\)

\(=x^5-2x^2+2-x^4+5x^3-x^2-5x+\dfrac{1}{3}\)

\(=x^5-x^4+5x^3-3x^2-5x+\dfrac{7}{3}\)

b: H(x)-Q(x)=-2³=-8

=>Q(x)=H(x)+8

\(=x^4-5x^3+x^2+5x-\dfrac{1}{3}+8\)

\(=x^4-5x^3+x^2+5x+\dfrac{23}{3}\)