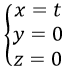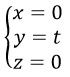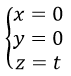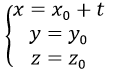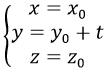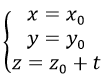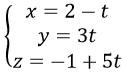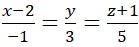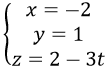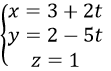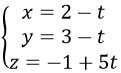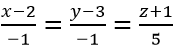Chọn D

Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi d nằm trên (P) hoặc d⊥(P)d⊥(P). Có đúng ko mn, mk nghĩ là thế, ai hc lớp 12 tl hộ mk vs.

a) Trục Ox là đường thẳng đi qua O(0, 0, 0) và nhận i→=(1,0,0) làm vectơ chỉ phương nên có phương trình tham số là:

* Tương tự, trục Oy có phương trình

Trục Oz có phương trình

b) Đường thẳng đi qua M0 (x0,y0,z0) song song với trục Ox sẽ có vectơ chỉ phương là i→(1,0,0) nên có phương trình tham số là:

tương tự ta có Phương trình của đường thẳng đi qua M0 (x0,y0,z0) và song song với Oy là:

phương trình đường thẳng đi qua M0 (x0,y0,z0) và song song với Oz là

c) Đường thẳng đi qua M(2, 0, -1) và có vectơ chỉ phương u→(-1,3,5) có phương trình tham số là

có phương trình chính tắc là

d) Đường thẳng đi qua N(-2, 1, 2) và có vectơ chỉ phương u→(0,0,-3) có phương trình tham số là

Đường thẳng này không có Phương trình chính tắc.

e) Đường thẳng đi qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x- 5y + 4= 0 nên nó nhận vectơ pháp tuyến của mặt phẳng này làn→(2,-5,0) là vectơ chỉ phương, nên ta có phương trình tham số là

Đường thẳng này không có Phương trình chính tắc.

f) Đường thẳng đi qau P(2, 3, -1) và Q(1, 2, 4) sẽ nhận PQ→(-1,-1,5) là vectơ chỉ phương, nên có phương trình tham số là

và có phương tình chính tắc là

ÔI THÔI CHẾT LM SAI

bùn mún gớt  nc mắt lun T~T

Sao buồn thế bạn xênh gái 

Gọi O là tâm hình bình hành; MN cắt AC tại J

Kẻ PE//SO thì E là trung điểm của OC suy ra \(IO=\frac{1}{2}PE=\frac{1}{4}SO\)

Gọi thể tích khối chóp là V

Ta có : \(\frac{V_{S.B'D'P}}{V_{S.BCD}}=\frac{SB'}{SB}.\frac{SD'}{SD}.\frac{SP}{SC}=\frac{3}{4}.\frac{3}{4}.\frac{1}{2}=\frac{9}{32}\)

suy ra \(V_{S.B'D'P}=\frac{9}{32}V_{S.BCD}=\frac{9}{64}V\)

Suy ra \(V_{BDD'BPC}=\frac{1}{2}V-\frac{9}{64}V=\frac{23}{64}V\)

pcm \(V_{MNDD'B'B}=\frac{9}{64}V\)

Ta có : \(V_{MNDD'B'B}=V_{J.BB'D'D}+V_{M.BB'J}+V_{N.DD'J}=V_{J.BB'D'D}+2.V_{M.BB'J}\)

Với \(V_{J.BB'D'D}=\frac{1}{2}V_{A.BB'D'D}=\frac{1}{2}\left[1-\left(\frac{3}{4}\right)^2\right].V_{A.SBD}\)\(=\frac{1}{2}.\frac{7}{16}.\frac{1}{2}V=\frac{7}{64}V\)

\(V_{M.BB'J}=V_{B'.BMJ}=\frac{1}{4}V_{S.BMJ}=\frac{1}{4}.\frac{1}{8}V_{S.ABD}\)\(=\frac{1}{4}.\frac{1}{8}.\frac{1}{2}V=\frac{1}{64}V\)

Vậy \(V_{MNDD'B'B}=V_{J.BB'D'D}+2.V_{M.BB'J}=\frac{7}{64}V+2\frac{1}{64}V=\frac{9}{64}V\left(đpcm\right)\)

Gọi H là khối đa diện nằm bên dưới mp(MNP)
Gọi h,S,V lần lượt là chiều cao, diện tích đáy, thể tích của khối chóp S.ABCD
Dễ thấy:

\(\hept{\begin{cases}S_{DNU}=S_{BMT}=S_{AMN}=\frac{1}{4}S_{ABD}=\frac{1}{8}S\\d\left(p;\left(ABCD\right)\right)=\frac{1}{2}h;d\left(q;\left(ABCD\right)\right)=d\left(r;\left(ABCD\right)\right)=\frac{1}{4}h\end{cases}}\)

Ta có: \(S_{CTU}=S+\frac{1}{8}S=\frac{9}{8}S\)

\(V_{P\cdot CTU}=\frac{1}{3}\cdot\frac{1}{2}h\cdot\frac{9}{8}S=\frac{9}{16}V\)

\(V_{Q\cdot UDN}=V_{R\cdot BMT}=\frac{1}{3}\cdot\frac{1}{4}\cdot\frac{1}{8}S=\frac{1}{32}V\)

\(V_H=V_{P\cdot CTU}-V_{Q\cdot UDN}-V_{R\cdot BMT}=\frac{1}{2}V\)

=> đpcm
Nguồn:  Chú lùn thứ 8 

chịuuuuuuu

ko biết

mình kkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooonnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnngggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg          tt                                                                           bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiieeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeettttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttttt

Thui khỏi bt lm òi * nhắn lun ko bt cho nhanh lại cn lm màu *

\(\frac{72}{55}\)

\(A=\frac{\frac{3}{2}+\frac{2}{5}+\frac{1}{10}}{\frac{3}{2}+\frac{2}{3}+\frac{1}{12}}\)

\(\Rightarrow A=\frac{\frac{15}{10}+\frac{4}{10}+\frac{1}{10}}{\frac{18}{12}+\frac{8}{12}+\frac{1}{12}}=\frac{\frac{20}{10}}{\frac{27}{12}}=\frac{2}{\frac{9}{4}}=2:\frac{9}{4}=2.\frac{4}{9}=\frac{8}{9}\)

! Ko bt có đúng ko nx  @@@

~ Học tốt 

# Chiyuki Fujito