Lời giải:

$A=x^2+2y^2+3z^2-2xy+2xz-2x-2y-8z+1998$

$2A=2x^2+4y^2+6z^2-4xy+4xz-4x-4y-16z+3996$

$=(x^2-4xy+4y^2)+(x^2+4xz+4z^2)+2z^2-4x-4y-16z+3996$

$=(x-2y)^2+(x+2z)^2-4x-4y-16z+2z^2+3996$

$=(x-2y)^2+2(x-2y)+1+(x+2z)^2-6(x+2z)+9+2z^2-4z+3986$

$=(x-2y+1)^2+(x+2z-3)^2+2(z^2-2z+1)+3984$

$=(x-2y+1)^2+(x+2z-3)^2+2(z-1)^2+3984\geq 3984$

$\Rightarrow A\geq 1992$

Vậy $A_{\min}=1992$
Giá trị này đạt tại $x-2y+1=x+2z-3=z-1=0$

$\Leftrightarrow x=y=z=1$

Lời giải:

$A=x^2+2y^2+3z^2-2xy+2xz-2x-2y-8z+1998$

$2A=2x^2+4y^2+6z^2-4xy+4xz-4x-4y-16z+3996$

$=(x^2-4xy+4y^2)+(x^2+4xz+4z^2)+2z^2-4x-4y-16z+3996$

$=(x-2y)^2+(x+2z)^2-4x-4y-16z+2z^2+3996$

$=(x-2y)^2+2(x-2y)+1+(x+2z)^2-6(x+2z)+9+2z^2-4z+3986$

$=(x-2y+1)^2+(x+2z-3)^2+2(z^2-2z+1)+3984$

$=(x-2y+1)^2+(x+2z-3)^2+2(z-1)^2+3984\geq 3984$

$\Rightarrow A\geq 1992$

Vậy $A_{\min}=1992$
Giá trị này đạt tại $x-2y+1=x+2z-3=z-1=0$

$\Leftrightarrow x=y=z=1$

5:

6:

Bài 5

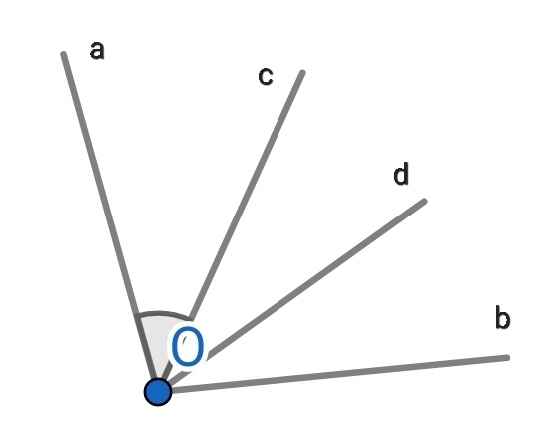
a) Do Oc nằm giữa hai tia Oa và Ob nên

∠aOc + ∠cOb = ∠aOb

⇒ ∠cOb = ∠aOb - ∠aOc

= 100⁰ - 40⁰

= 60⁰

b) Do Od là tia phân giác của ∠cOb (gt)

⇒ ∠cOd = ∠cOb : 2

= 60⁰ : 2

= 30⁰

Bạn kiểm tra lại đề giúp mình ạ !

đề cho thế á

Ta có: x³ + 3x² + 3x² + 9x + 2x +6

= x².(x+3) + 3x.(x+3) + 2.(x+3)

= (x²+3x+2). (x+3)

= ( x² + x +2x +2 ). ( x+3)

=(x+1).(x+2).(x+3)

TICK CHO MIK NHA

Bạn hãy xoá câu hỏi ở trên ik.

Số tiền mua bút bi và bút chì là \(279000-45000\cdot3=144000\left(đồng\right)\)

Tổng số bút bi và bút chì màu là 36 chiếc nên x+y=36

Số tiền mua bút bi là 3600x(đồng)

Số tiền mua bút chì màu là 5000y(đồng)

Tổng số tiền là 144000 đồng nên 3600x+5000y=144000

=>36x+50y=144

=>18x+25y=72

Do đó, hệ hai phương trình là: \(\left\{{}\begin{matrix}x+y=36\\18x+25y=72\end{matrix}\right.\)

Lời giải:

$C=(x^2+4y^2+9z^2-4xy+6xz-12yz)+2y^2+5z^2+4yz$

$=(x-2y+3z)^2+2(y^2+z^2+2yz)+3z^2$

$=(x-2y+3z)^2+2(y+z)^2+3z^2\geq 0$ với mọi $x,y,z$

Vậy $C_{\min}=0$.

Giá trị này đạt tại $x-2y+3z=y+z=z=0$

$\Leftrightarrow x=y=z=0$

= 3 x 100 - 300 x 3 - 9 x 3 + 3 x 15

= 3 x (100 - 300 - 9 + 15)

= 3 x -194 

= -582

\(3\cdot100-100\cdot9-9\cdot3+3\cdot15\)

=300-900-27+45

=-600+18

=-582

a: \(2^5\cdot8^4=2^5\cdot2^{12}=2^{17}\)

b: \(25^6\cdot125^3=\left(5^2\right)^6\cdot\left(5^3\right)^3=5^{12}\cdot5^9=5^{21}\)

c: \(625^3:25^3=\left(625:25\right)^3=25^3\)

x:6+17567=30876

=>x:6=30876-17567=13309

=>\(x=13309\times6=79854\)

x:6+17568=30876

=>x:6=30876-17568=13308

=>\(x=13308\times6=79848\)

\(X:6+17568=30876\)

\(X:6=30876-17568\)

\(X:6=13308\)

\(X=13308.6\)

\(X=79848\)