Trên nửa đường tròn tâm O đường kính AB với AB = 2022, lấy điểm C (C khác A và B), từ C kẻ CH vuông góc với AB (H thuộc AB). Gọi D là điểm bất kỳ trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E. a) Chứng minh tứ giác BHDE là tứ giác nội tiếp; b) Chứng minh: AD.EC=CD.AC; c) Chứng minh: AD.AE+BH.BA=2022^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


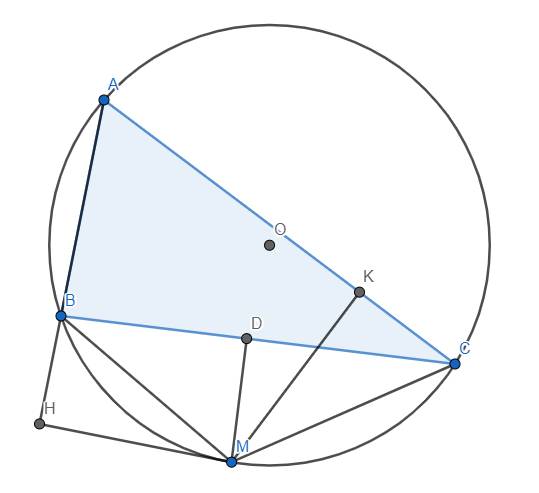
a) Theo đề bài, ta thấy \(\widehat{AHM}=\widehat{AKM}=90^o\) nên dễ dàng suy ra tứ giác AHMK nội tiếp do 2 góc đối bù nhau.
b) Do tứ giác AHMK nội tiếp nên \(\widehat{HMK}+\widehat{A}=180^o\). Tứ giác ABMC nội tiếp nên \(\widehat{BMC}+\widehat{A}=180^o\). Từ đó suy ra \(\widehat{HMK}=\widehat{BMC}\) hay \(\widehat{BMH}=\widehat{CMK}\). Lại có \(\widehat{MHB}=\widehat{MKC}=90^o\) nên \(\Delta MHB~\Delta MKC\left(g.g\right)\) \(\Rightarrow\dfrac{MH}{MK}=\dfrac{MB}{MC}\) \(\Rightarrowđpcm\)

Lời giải:
Trừ theo vế 2 pt trên ta có:
$x^3-y^3=5y-5x$
$\Leftrightarrow (x-y)(x^2+xy+y^2)+5(x-y)=0$
$\Leftrightarrow (x-y)(x^2+xy+y^2+5)=0$
Ta thấy: $x^2+xy+y^2+5=(x+\frac{y}{2})^2+\frac{3y^2}{4}+5\geq 5>0$ với mọi $x,y$
$\Rightarrow x-y=0$
$\Leftrightarrow x=y$.
Thay vào pt (1): $x^3=3x+8x=11x$
$\Leftrightarrow x(x^2-11)=0$
$\Leftrightarrow x\in\left\{0; \pm \sqrt{11}\right\}$
Vậy........

Yêu cầu đề bài là gì bạn nên ghi đầy đủ để được hỗ trợ tốt hơn.

\(\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}}=\left(\dfrac{x-1}{\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}.\dfrac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-1\)

a.
\(DH\perp AB\left(gt\right)\Rightarrow\widehat{DHB}=90^0\Rightarrow D;H;B\) cùng thuộc đường tròn đường kính DB
\(\widehat{AEB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O)) \(\Rightarrow\widehat{DEB}=90^0\)
\(\Rightarrow D;E;B\) cùng thuộc đường tròn đường kính DB
\(\Rightarrow\) Tứ giác BHDE nội tiếp đường tròn đường kính DB
b.
\(\widehat{ACB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O))
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ \(\widehat{BAC}\))
Mà \(\widehat{ABC}=\widehat{AEC}\) (cùng chắn cung AC của (O)
\(\Rightarrow\widehat{ACH}=\widehat{AEC}\)
Xét hai tam giác ADC và ACE có: \(\left\{{}\begin{matrix}\widehat{ACH}=\widehat{AEC}\left(cmt\right)\\\widehat{CAD}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g.g\right)\Rightarrow\dfrac{AD}{AC}=\dfrac{CD}{EC}\Rightarrow AD.EC=CD.AC\)
c.
Cũng theo cmt \(\Delta ADC\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}\Rightarrow AD.AE=AC^2\)
Áp dụng hệ thức lượng trong tam giác vuông ABC với đường cao CH:
\(BC^2=BH.BA\)
\(\Rightarrow AD.AE+BH.BA=AC^2+BC^2=AB^2=2022^2\)