. Cho số a và ba số b, c, d khác a và thỏa mãn điều kiện c + d = 2b. Giải phương trình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. y(y+1)-5y-5 2. 4x3=x
=y(y+1)-(5y+5) <=>4x3-x=0
=y(y+1)-5(y+1) <=>x(4x2-1)=0
=(y+1)(y-5) <=>x(4x2-1)=0
<=>\(\orbr{\begin{cases}x=0\\4x^2-1=0\end{cases}}\)=\(\orbr{\begin{cases}x=0\\4x^2=1\end{cases}}\)=\(\orbr{\begin{cases}x=0\\x^2=\frac{1}{4}\end{cases}}\)=\(\orbr{\begin{cases}x=0\\x=+_-\frac{1}{2}\end{cases}}\)
3. M= (x+3)2 -(4x+1)-x(2x+1)
M= (x2+6x+9)-4x-1-2x2-x
M=x2+6x+9-4x-1-2x2-x
M= -x2+x+8

Câu 6 :
Lỗi nên không vẽ được hình nha bạn !
Xét \(\Delta ABC\)có MN // BC
Theo Ta - lét ta có :
\(\frac{AM}{AB}=\frac{MN}{BC}=\frac{1}{3}\)
=> \(\frac{2}{BC}=\frac{1}{3}\Rightarrow BC=6cm\)
Câu 3 :
a2 .6 = 216 -> a2 =36=> a = 6
-> V khối lập phương đó = 6 . 6. 6 =216 cm3
Câu 1 :
ĐKXĐ
\(\hept{\begin{cases}x-1\ne0\\x-2\ne0\\x^2-3x+2\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x-1\ne0\\x-2\ne0\\\left(x-1\right)\left(x-2\right)\ne0\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ne1\\x\ne2\end{cases}}\)
Vậy x\(\ne1;x\ne2\)

a) \(xy+x+2y=-2\)
\(xy+x+2y+2=0\)
\(x\left(y+1\right)+2\left(y+1\right)=0\)
\(\left(x+2\right)\left(y+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\y+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-2\\y=-1\end{cases}}}\)
b) Chia cả hai vế cho x^2 ta được
\(x^2-3x+4-\frac{3}{x}+\frac{1}{x^2}=0\)
\(\left(x^2+\frac{1}{x^2}\right)-3\left(x+\frac{1}{x}\right)+4=0\)
Đặt a=x+1/x thì => x^2 +1/x^2=a^2-2, ta được
\(a^2-3a+2=0\)
\(a\left(a-2\right)-\left(a-2\right)=0\)
\(\left(a-1\right)\left(a-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=1\\a=2\end{cases}}\)
Với a=1 ta có: \(x^2-x+1=0\)vô nghiệm
Với a=2 ta có: \(x^2-2x+1=0\Rightarrow x=1\)
Vậy nghiệm của pt là x=1

Phạm tuấn Đạt
cái này áp dụng t/c tam giác đồng dạng :Tỉ số diện tích của 2 tam giác đồng dạng bằng bình phương tỉ số đồng dạng

- Ta có: \(\frac{x+4}{x-2}=\frac{-3}{4}\)
\(\Rightarrow4.\left(x+4\right)=-3.\left(x-2\right)\)
\(\Leftrightarrow4x+16=-3x+6\)
\(\Leftrightarrow4x+3x=6-16\)
\(\Leftrightarrow7x=-10\)
\(\Leftrightarrow x=-\frac{10}{7}\)
Vậy \(S=\left\{-\frac{10}{7}\right\}\)

Gọi x (km) là quảng đường AB (x > 0)
Thời gian xe máy đi từ A đến B là:\(\frac{x}{50}\)(h)
Thời gian xe máy đi từ B về A là:\(\frac{x}{40}+\frac{1}{4}\)(h)
Biết thời gian cả đi cả về là 2h30' , ta có phương trình
\(\frac{x}{50}+\left(\frac{x}{40}+\frac{1}{4}\right)=\frac{15}{6}\)
\(\Leftrightarrow\frac{x}{50}+\frac{x}{40}+\frac{1}{4}=\frac{15}{6}\)
\(\Leftrightarrow\frac{12x}{12.50}+\frac{15x}{15.40}+\frac{150}{600}=\frac{100.15}{100.6}\)
\(\Leftrightarrow12x+15x+150=1500\)
\(\Leftrightarrow x\left(12+15\right)+150=1500\)
\(\Leftrightarrow x.27=1500-150\)
\(\Leftrightarrow x.27=1350\)
\(\Leftrightarrow x=\frac{1350}{27}\Leftrightarrow x=50\)(TMĐK)
Vậy quảng đường AB dài 50km
#Học tốt!!!
~NTTH~
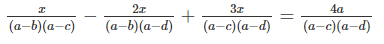
Lm hộ mình nha bạn