Câu 5:

Gọi hàm số bậc nhất cần tìm có dạng là y=ax+b(\(a\ne0\))

Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-2x+1 nên \(\left\{{}\begin{matrix}a=-2\\b\ne1\end{matrix}\right.\)

Vậy: y=-2x+b

Thay x=-1 và y=3 vào y=-2x+b, ta được:

\(\left(-2\right)\cdot\left(-1\right)+b=3\)

=>b+2=3

=>b=1(loại)

Vậy: KHông có hàm số bậc nhất nào thỏa mãn yêu cầu đề bài

Câu 4: 

Gọi hàm số bậc nhất cần tìm có dạng là y=ax+b(\(a\ne0\))

Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-2x+1 nên \(\left\{{}\begin{matrix}a=-2\\b\ne1\end{matrix}\right.\)

Vậy: y=-2x+b

Thay x=-1 và y=4 vào y=-2x+b, ta được:

\(\left(-2\right)\cdot\left(-1\right)+b=4\)

=>b+2=4

=>b=2(nhận)

vậy: y=-2x+2

$b$ ở chỗ nào vậy bạn?

b nằm ở đâu trong PTĐT $y=ax+20$ vậy bạn?

Em k biết nữa ak

a: Xét tứ gíc AMDN có \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)

nên AMDN là hình chữ nhật

=>AD=MN

b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có

\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HCA}\right)\)

Do đó: ΔHBA~ΔHAC

=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)

=>\(HA^2=HB\cdot HC\)

c: \(HA^2=HB\cdot HC\)

=>\(HA^2=2\cdot8=16=4^2\)

=>HA=4(cm)

ΔHAB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(AB=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\)

ΔHAC vuông tại H

=>\(HA^2+HC^2=AC^2\)

=>\(AC=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

a: a: Xét ΔABC và ΔAED có

\(\dfrac{AB}{AE}=\dfrac{AC}{AD}\left(\dfrac{15}{5}=\dfrac{21}{7}=3\right)\)

\(\widehat{BAC}\) chung

Do đó: ΔABC~ΔAED

Vì \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)

nên \(AB\cdot AD=AE\cdot AC\)

b: \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)

=>\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)

Xét ΔABE và ΔACD có

\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)

\(\widehat{BAE}\) chung

Do đó: ΔABE~ΔACD

=>\(\widehat{ABE}=\widehat{ACD};\widehat{AEB}=\widehat{ADC}\)

c: Xét ΔOBD và ΔOCE có

\(\widehat{OBD}=\widehat{OCE}\)

\(\widehat{BOD}=\widehat{COE}\)(hai góc đối đỉnh)

Do đó: ΔOBD~ΔOCE
=>\(\dfrac{OB}{OC}=\dfrac{OD}{OE}\)

=>\(OB\cdot OE=OD\cdot OC\)

Đề hiển thị lỗi. Bạn xem lại nhé.

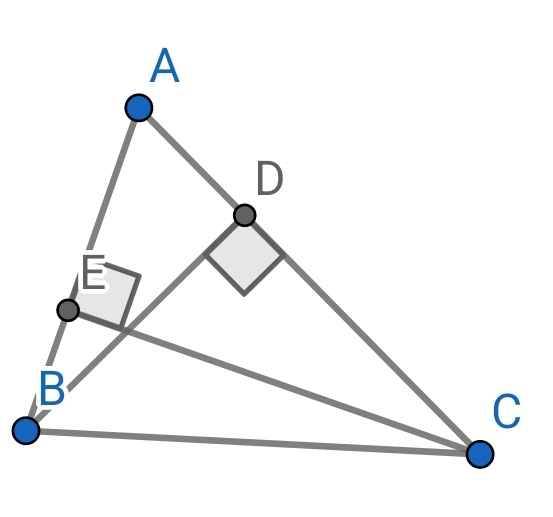
Xét hai tam giác vuông: ∆ABD và ∆ACE có:

A chung

⇒ ∆ABD ∽ ∆ACE (g-g)

⇒ AB/AC = AD/AE

⇒ AD = AB/AC . AE

= 4/6 . 3

= 2 (cm)

Veve

Lời giải:
Gọi số rổ là $a$ (chiếc)

Theo bài ra ta có: $3a+4=4(a-1)$

$\Leftrightarrow a=8$

Đáp án B.

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có

\(\widehat{ABH}\) chung

Do đó: ΔABH~ΔCBA

=>\(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)

=>\(BA^2=BH\cdot BC\)

b: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét ΔCAB có CD là phân giác

nên \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\)

=>\(\dfrac{AD}{8}=\dfrac{BD}{10}\)

=>\(\dfrac{AD}{4}=\dfrac{BD}{5}\)

mà AD+BD=AB=6cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{4}=\dfrac{BD}{5}=\dfrac{AD+BD}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)

=>\(AD=4\cdot\dfrac{2}{3}=\dfrac{8}{3}\left(cm\right);BD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)