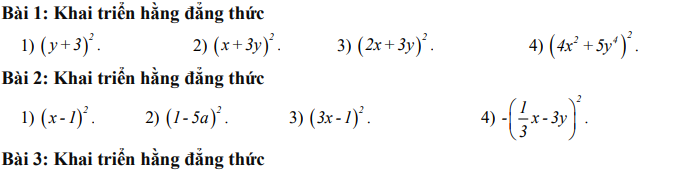\(\left(x^2+4y^2-4xy\right):\left(x-2y\right)=\left(x-2y\right)^2:\left(x-2y\right)=x-2y\)

\(A=-\left(x^2-6x+9\right)=-\left(x-3\right)^2\)

Do \(\left(x-3\right)^2\ge0;\forall x\Rightarrow-\left(x-3\right)^2\le0;\forall x\)

\(\Rightarrow A\le0\Rightarrow A_{max}=0\) khi \(x=3\)

\(B=4x^2-4x+1+14=\left(2x-1\right)^2+14\)

Do \(\left(2x-1\right)^2\ge0;\forall x\Rightarrow\left(2x-1\right)^2+14\ge14;\forall x\)

\(\Rightarrow B_{min}=14\) khi \(2x-1=0\Rightarrow x=\dfrac{1}{2}\)

a.

\(\left(x+2y\right)^2-\left(x-2y\right)^2=\left(x+2y+x-2y\right)\left(x+2y-x+2y\right)=2x.4y=8xy\)

b.

\(\left(3x+2y\right)^2-\left(3x+2y\right)\left(6y-4x\right)+\left(2x-3y\right)^2\)

\(=\left(2x+3y\right)^2+2\left(2x+3y\right)\left(2x-3y\right)+\left(2x-3y\right)^2\)

\(=\left(2x+3y+2x-3y\right)^2\)

\(=\left(4x\right)^2=16x^2\)

Chắc em ghi nhầm đề, hoặc là số giữa là \(2\left(2+3x\right)\left(1-2y\right)\), hoặc là số cuối là \(\left(2x-1\right)^2\)

Sửa đề; BN cắt AH tại G

a: Xét ΔNGA và ΔNKC có

NG=NK

\(\widehat{GNA}=\widehat{KNC}\)(hai góc đối đỉnh)

NA=NC

Do đó: ΔNGA=ΔNKC

=>\(\widehat{NGA}=\widehat{NKC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên GA//KC

b: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

Xét ΔABC có

AH,BN là các đường trung tuyến

AH cắt BN tại G

Do đó: G là trọng tâm của ΔABC

=>BG=2GN

mà GK=2GN

nên BG=GK

=>G là trung điểm của BK

c: Xét ΔABC có

G là trọng tâm

M là trung điểm của AB

Do đó: C,G,M thẳng hàng

Xét ΔABC có

G là trọng tâm

AH là đường trung tuyến

Do đó: AG=2GH

Xét ΔGCB có

GH là đường trung tuyến

GH là đường cao

Do đó: ΔGBC cân tại G

=>GB=GC

Xét ΔGHB có HG+HB>GB

=>2(HG+HB)>2GB

=>GA+BC>2GC

=>GA+BC>2*2GM=4GM

Gọi chiều dài màn hình là `x` (cm) 

ĐK: `x>0` 

Đổi: 17inch ≃ 43,18 (cm) 

Chiều cao màn hình là: `5/8x(cm)` 

Áp dụng định lý Pythagore ta có: 

\(x^2+\left(\dfrac{5}{8}x\right)^2=43,18^2\\ < =>x^2+\dfrac{25}{64}x^2=1864,5124\\ < =>\dfrac{79}{64}x^2=1864,5124\\ < =>x^2\approx1510,4\\ < =>x\approx38,9\left(cm\right)\left(x>0\right)\)

=> Chiều cao của màn hình là: `5/8*38,9≃24,3(cm)` 

Vậy: 

Gọi x (cm) là chiều rộng màn hình (x > 0)

Chiều dài màn hình là:

  Đổi 17 inch ≈ 43,2 cm

  Theo đề bài, ta có phương trình:

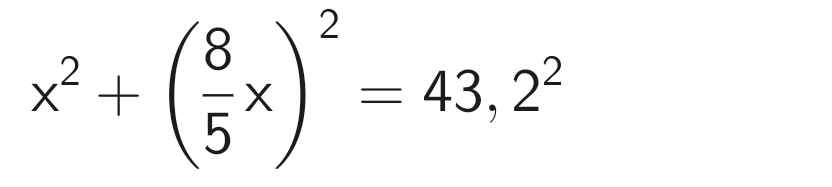
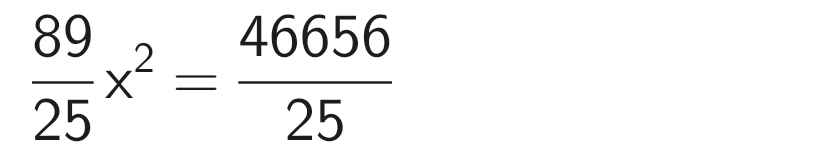
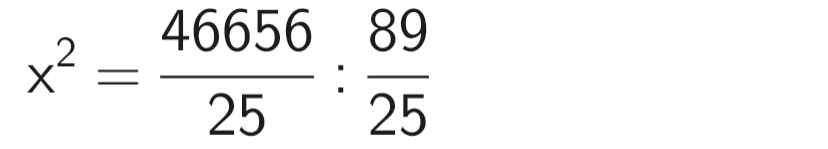
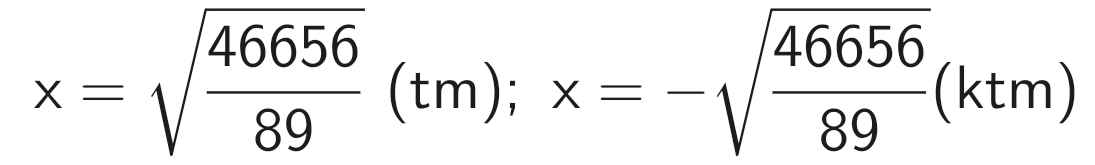
⇒ x ≈ 22,9 (cm)

Vậy chiều rộng màn hình là 22,9 cm, chiều dài màn hình là 22,9.1,6 ≈ 36,6 cm

Bài 1:

\(1,\left(y+3\right)^2\\ =y^2+2\cdot y\cdot3+3^2\\ =y^2+6y+9\\ 2,\left(x+3y\right)^2\\ =x^2+2\cdot x\cdot3y+\left(3y\right)^2\\ =x^2+6xy+9y^2\\ 3,\left(2x+3y\right)^2\\ =\left(2x\right)^2+3\cdot2x\cdot3y+\left(3y\right)^2\\ =4x^2+18xy+9y^2\\ 4,\left(4x^2+5y^4\right)\\ =\left(4x^2\right)^2+2\cdot4x^2\cdot5y^4+\left(5y^4\right)^2\\ =16x^4+40x^2y^4+25y^8\) 

Bài 2: 

\(1,\left(x-1\right)^2\\ =x^2-2\cdot x\cdot1+1^2\\ =x^2-2x+1\\ 2,\left(1-5a\right)^2\\ =1^2-2\cdot1\cdot5a+\left(5a\right)^2\\ =1-10a+25a^2\\ 3,\left(3x-1\right)^2\\ =\left(3x\right)^2-2\cdot3x\cdot1+1^2\\ =9x^2-6x+1\\ 4,-\left(\dfrac{1}{3}x-3y\right)^2\\ =-\left[\left(\dfrac{1}{3}x\right)^2-2\cdot\dfrac{1}{3}x\cdot3y+\left(3y\right)^2\right]\\ =-\left(\dfrac{1}{9}x^2-2xy+9y^2\right)\\ =-\dfrac{1}{9}x^2+2xy-9y^2\)

mình cần gấp áa

a: X,Y trái dấu

=>XY<0

=>\(-2abc^3\cdot3a^2b^3c^5< 0\)

=>\(-6a^3b^4c^8< 0\)

=>\(a^3>0\)

=>a>0

b: X,Y cùng dấu

=>X*Y>0

=>\(-2abc^3\cdot3a^2b^3c^5>0\)

=>\(-6a^3b^4c^8>0\)

=>\(a^3< 0\)

=>a<0

c: \(X\cdot Y=-5a^2n\cdot b\cdot3a^4n\cdot b^5=-15a^6n^2b^6< =0\forall a,b,n\)

=>X và Y không thể cùng có giá trị âm

a: Xét ΔMNP có \(\dfrac{MH}{MN}=\dfrac{MK}{MP}\)

nên HK//PN

Xét tứ giác NHKP có HK//NP

nên NHKP là hình thang

Hình thang NHKP có \(\widehat{HNP}=\widehat{KPN}\)(ΔMNP cân tại M)

nên NHKP là hình thang cân