cho hai đa thức: p(x)=3x2+4x-x3-1 q(x)=x2+x3+4x+8+-2x3 tìm nghiệm M(x) biết M(x)=p(x)-q(x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\left(x+11\right)-x^2+x=12\)
=>\(x^2+11x-x^2+x=12\)
=>12x=12
=>x=1

A = x² - 4x + 5
= x² - 2x - 2x + 4 + 1
= (x² - 2x) - (2x - 4) + 1
= x(x - 2) - 2(x - 2) + 1
= (x - 2)(x - 2) + 1
= (x - 2)² + 1
Do (x - 2)² ≥ 0
(x - 2)² + 1 > 0
Vậy đa thức A không có nghiệm
Đặt A(x)=0
=>\(x^2-4x+5=0\)
=>\(x^2-4x+4+1=0\)
=>\(\left(x-2\right)^2+1=0\)(vô lý)
=>A(x) không có nghiệm

a: Số tiền mua 5kg táo là 5x(đồng)
Số tiền mua 4kg nho là 4y(đồng)
Tổng số tiền phải trả là 5x+4y(đồng)
Bậc là 1
b: Khối lượng táo có trong 10 hộp táo là \(10\cdot10=100\left(kg\right)\)
Khối lượng nho có trong 10 hộp là \(10\cdot12=120\left(kg\right)\)
Tổng số tiền phải trả là 100x+120y(đồng)
Bậc là 1

a: Chiều rộng bể nước là x-3(m)
Chiều cao của bể nước là x-3-2=x-5(m)
b: Thể tích bể nước là:
\(x\left(x-3\right)\left(x-5\right)\)
\(=x\left(x^2-8x+15\right)\)
\(=x^3-8x^2+15x\)

a: 30p=0,5 giờ
Tổng thời gian xe máy đi được là x(giờ)
=>Độ dài quãng đường xe máy đi được là \(Q\left(x\right)=50x\left(km\right)\)
Tổng thời gian ô tô đi là x-0,5(giờ)
=>Độ dài quãng đường ô tô chạy là 70(x-0,5)(km)
b: Để hai xe gặp nhau thì 70(x-0,5)=50x
=>70x-35=50x
=>20x=35
=>x=1,75(nhận)
Vậy: Hai xe gặp nhau sau 1,75 giờ
Chỗ gặp nhau cách A là: 70*1,75=122,5 km
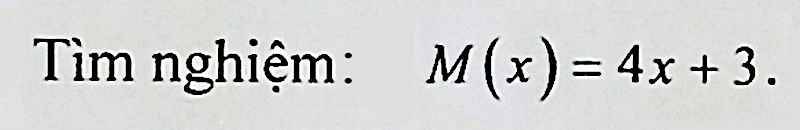
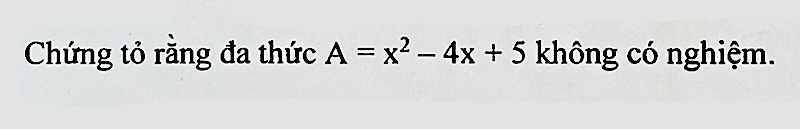
M(x) = p(x) - q(x)
= (3x² + 4x - x³ - 1) - (x² + x³ + 4x + 8 - 2x³)
= 3x² + 4x - x³ - 1 - x² - x³ - 4x - 8 + 2x³
= (-x³ - x³ + 2x³) + (3x² - x²) + (4x - 4x) + (-1 + 8)
= 2x² + 7
Cho M(x) = 0
2x² + 7 = 0
2x² = 0 - 7
2x² = -7
x² = -7/2 (vô lý)
Vậy đa thức M(x) không có nghiệm