\(\dfrac{34}{62}+a=\dfrac{1}{3}\\ =>\dfrac{17}{31}+a=\dfrac{1}{3}\\ =>a=\dfrac{1}{3}-\dfrac{17}{31}\\ =>a=\dfrac{31}{93}-\dfrac{51}{93}\\ =>a==\dfrac{-20}{93}\)

Mua 6 bút bi và 15 quyển vở hết:

\(3\times74000=222000\left(đ\right)\)

Mua 6 bút bi và 8 quyển vở hết: 

\(2\times69000=138000\left(đ\right)\)

Mua 7 quyển vở hết: 

\(222000-138000=84000\left(đ\right)\)

Giá của 1 quyển vở là:

\(84000:7=12000\left(đ\right)\)

Giá của một quyển vở là:

\(\left(74000-5\times12000\right):2=7000\left(đ\right)\)

Giá tiền của 6 bút bi và 15 quyển vở là 74000x3=222000 đồng

Giá tiền của 6 bút bi và 8 quyển vở là 69000x2=138000 đồng

Giá tiền của 7 quyển vở là:

222000-138000=84000 đồng

Giá tiền của 1 quyển vở là 84000:7=12000 đồng

Giá tiền của 2 bút bi là 74000-5x12000=14000 đồng

Giá tiền của 1 bút bi là 14000:2=7000 đồng

\(4-x^2+2x\\ =\left(-x^2+2x-1\right)+5\\ =-\left(x^2-2x+1\right)+5\\ =-\left(x-1\right)^2+5\)

Ta có: \(-\left(x-1\right)^2\le0\forall x\)

\(=>-\left(x-1\right)^2+5\le5\forall x\)

Dấu "=" xảy ra: `x-1=0<=>x=1`

Vậy: ... 

\(\left(2a+b\right)^2-\left(2b+a\right)^2\\ =\left[\left(2a+b\right)-\left(2b+a\right)\right]\left[\left(2a+b\right)+\left(2b+a\right)\right]\\ =\left(2a+b-2b-a\right)\left(2a+b+2b+a\right)\\ =\left(a-b\right)\left(3a+3b\right)\\ =3\left(a-b\right)\left(a+b\right)\)

\(-\dfrac{13}{38}=\dfrac{-13\cdot88}{38\cdot88}=\dfrac{-1144}{3344};\dfrac{29}{-88}=\dfrac{29\cdot\left(-38\right)}{\left(-88\right)\left(-38\right)}=\dfrac{-1102}{3344}\)

mà -1144<-1102

nên \(-\dfrac{13}{38}< \dfrac{29}{-88}\)

Ta có:

\(\dfrac{13}{38}>\dfrac{13}{39}=>\dfrac{-13}{38}< \dfrac{-13}{39}=-\dfrac{1}{3}\\\dfrac{29}{88} < \dfrac{29}{87}=>\dfrac{-29}{88}>-\dfrac{28}{87}=-\dfrac{1}{3}\)

\(=>\dfrac{-13}{38}< -\dfrac{1}{3}< \dfrac{-29}{88}\)

Ta có: 

\(\left(x+y\right)^2\ge0\forall x,y\\ \left(x+1\right)^2\ge0\forall x\\ \left(y-2\right)^2\ge0\forall y\)

\(L=\left(x+y\right)^2+\left(x+1\right)^2+\left(y-2\right)^2\ge0\forall x,y\)

Dấu "=" xảy: \(\left\{{}\begin{matrix}x+y=0\\x+1=0\\y-2=0\end{matrix}\right.\Leftrightarrow x,y\in\varnothing\)

=> L không có GTNN 

b: \(\dfrac{-8}{-20}=\dfrac{18}{45};\dfrac{-8}{18}=\dfrac{-20}{45};\dfrac{-20}{-8}=\dfrac{45}{18};\dfrac{18}{-8}=\dfrac{45}{-20}\)

c: \(\dfrac{4}{8}=\dfrac{16}{32};\dfrac{4}{16}=\dfrac{8}{32};\dfrac{8}{4}=\dfrac{32}{16};\dfrac{16}{5}=\dfrac{32}{8}\)

\(\dfrac{4}{32}=\dfrac{8}{64};\dfrac{4}{8}=\dfrac{32}{64};\dfrac{8}{4}=\dfrac{64}{32};\dfrac{32}{4}=\dfrac{64}{8}\)

mik cần gấp

TH1: x<-2

Phương trình sẽ trở thành: \(3x\left(-x-1\right)-2x\left(-x-2\right)=12\)

=>\(-3x^2-3x+2x^2+4x-12=0\)

=>\(-x^2+x-12=0\)

\(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-12\right)=1-4\cdot12=1-48=-47< 0\)

=>Phương trình vô nghiệm

TH2: -2<=x<-1

Phương trình sẽ trở thành:

\(3x\left(-x-1\right)-2x\left(x+2\right)=12\)

=>\(-3x^2-3x-2x^2-4x-12=0\)

=>\(5x^2+7x+12=0\)

\(\text{Δ}=7^2-4\cdot5\cdot12=49-20\cdot12=49-240=-191< 0\)

=>Phương trình vô nghiệm

TH3: x>=-1

Phương trình sẽ trở thành:

\(3x\left(x+1\right)-2x\left(x+2\right)=12\)

=>\(3x^2+3x-2x^2-4x-12=0\)

=>\(x^2-x-12=0\)

=>(x-4)(x+3)=0

=>\(\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\)

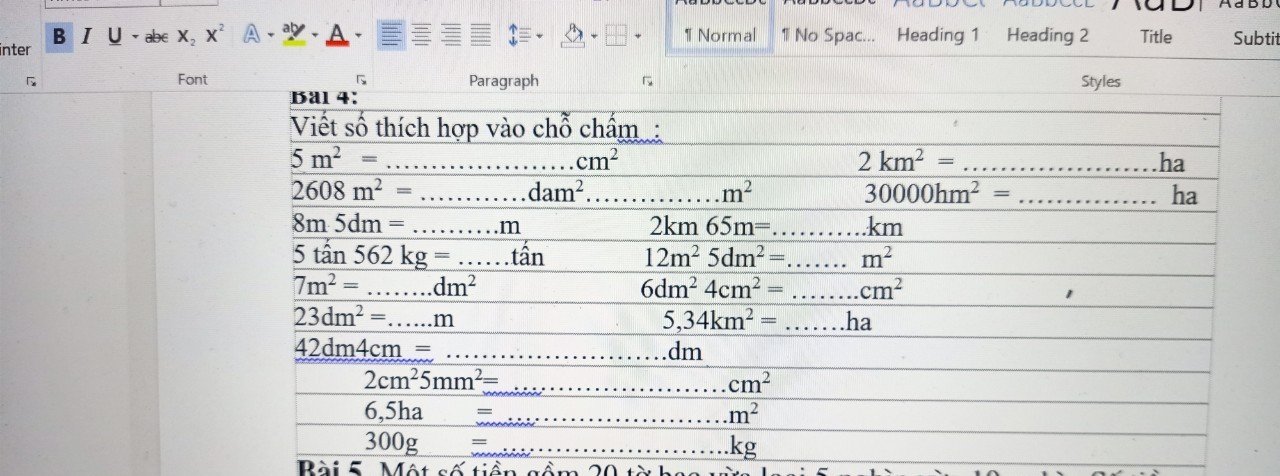
\(5m^2=50000cm^2\) \(2km^2=200ha\)

\(2608m^2=26dam^28m^2\)

\(30000hm^2=30000ha\)

\(8m5dm=8,5m\)

2km65m=2,065km

5 tấn 562kg=5,562 tấn

\(12m^25dm^2=12,05m^2\)

\(7m^2=700dm^2\)

\(6dm^24cm^2=604cm^2\)

\(5,34km^2=534ha\)

42dm4cm=42,4dm

\(2cm^25mm^2=2,05cm^2\)

\(6,5ha=65000m^2\)

300g=0,3kg

\(5m^2=50000cm^2\\ 2km^2=200ha\\ 2608m^2=26,08dam^2\\3000hm^2=3000ha\\ 8m5dm=8,5m\\ 2km65m=2,065km\)

5 tấn 562 kg = 5,562 tấn 

\(12m^25dm^2=12,05m^2\)