cho mình hỏi với là b= x mũ2-2x+1/x+1
tìm x thuộc z để b là số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

192 = 2.96= 2. (8.12)
Vì: 12= 8+4
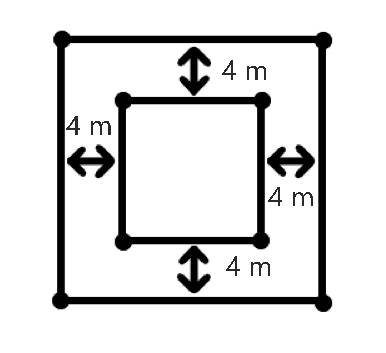
Vậy ao cũ có cạnh bằng 8m
Diện tích ao cũ:
8.8 = 64(m2)

A = \(\dfrac{\dfrac{2}{3}-\dfrac{2}{13}+\dfrac{2}{2023}}{\dfrac{4}{3}-\dfrac{4}{13}+\dfrac{4}{2023}}\)
A = \(\dfrac{2.\left(\dfrac{1}{3}-\dfrac{1}{13}+\dfrac{1}{2023}\right)}{4.\left(\dfrac{1}{3}-\dfrac{1}{13}+\dfrac{1}{2023}\right)}\)
A = \(\dfrac{1}{2}\)

\(\dfrac{99}{98}-\dfrac{98}{97}+\dfrac{1}{97\cdot98}\)
\(=\dfrac{99\cdot97}{98\cdot97}-\dfrac{98\cdot98}{97\cdot98}+\dfrac{1}{97\cdot98}\)
\(=\dfrac{99\cdot97-98^2+1}{98\cdot97}\)
\(=\dfrac{\left(98+1\right)\left(98-1\right)-98^2+1}{98\cdot97}\)
\(=\dfrac{98^2-1-98^2+1}{98\cdot97}\)
\(=\dfrac{0}{97\cdot98}\)
\(=0\)
\(\dfrac{99}{98}-\dfrac{98}{97}+\dfrac{1}{97.98}=\dfrac{99.97}{97.98}-\dfrac{98.98}{97.98}+\dfrac{1}{97.98}\)
\(=\dfrac{99.97-98.98+1}{97.98}=\dfrac{\left(98+1\right).\left(98-1\right)-98^2+1}{97.98}\)
\(=\dfrac{98^2-1-98^2+1}{97.98}=0\)

\(63+27.97+18=63+18+27.97=81++27.97=27.3+27.97=27.\left(3+97\right)=27.100=2700\)

\(2^{10}+2^{11}+2^{12}=2^8\left(2^2+2^3+2^4\right)=2^8.\left(4+8+16\right)=2^8.28⋮28\left(đpcm\right)\)
\(2^{10}+2^{11}+2^{12}⋮28\\ \Rightarrow2^8+\left(4+8+16\right)\\ \Rightarrow2^8+28\\ \)
\(\)Vì \(28⋮28\\ \Rightarrow2^{10}+2^{11}+2^{12}⋮28.\)

1. \(x⋮15\Rightarrow x\in B\left(15\right)=\left\{0;15;30;45;60;75;90;105;120;135;150;...\right\}\)
mà \(45< x< 136\)
\(\Rightarrow x\in\left\{60;75;90;105;120;135\right\}\)
2.
\(18⋮x\Rightarrow x\in U\left(18\right)=\left\{1;2;3;6;18\right\}\)
mà \(x>7\Rightarrow\Rightarrow x\in\left\{18\right\}\)

1. A={0;7;14;21;28}
2. B={0;10;20;30;40}
1.
5 phần tử là 5 số nhỏ nhất là bội của 7
\(B\left(7\right)=\left\{0;7;14;21;28\right\}\)
2.
5 phần tử là 5 số nhỏ nhất là bội của 10
\(B\left(10\right)=\left\{0;10;20;30;40\right\}\)
Bạn xem lại đề
B = \(\dfrac{x^2-2x+1}{x+1}\)
Với \(x\in\)Z, để B là số nguyên thì \(x^2-2x+1\)⋮ \(x+1\)
Theo Bezout ta có: F(\(x\)) = \(x^2\) - 2\(x\) + 1 ⋮ \(x+1\) ⇔ F(\(-1\)) ⋮ \(x+1\)
⇒ (-1)2 - 2.(-1) + 1 ⋮ \(x\) + 1 ⇔ 4 ⋮ \(x\) + 1
⇔ \(x\) + 1 \(\in\) Ư(4) = { -4; -2; -1; 1; 2; 4}
\(\Leftrightarrow\) \(x\) \(\in\) { -5; -3; -2; 0; 1; 3}