a) Do MP // HK (gt)

\(HK\perp HI\) (\(\Delta HIK\) vuông tại H)

\(\Rightarrow MP\perp HI\)

\(\Rightarrow\widehat{MPH}=90^0\)

Do MQ // HI (gt)

\(HI\perp HK\left(cmt\right)\)

\(\Rightarrow MQ\perp HK\)

\(\Rightarrow\widehat{MQH}=90^0\)

Tứ giác HQMP có:

\(\widehat{MQH}=\widehat{MPH}=\widehat{PAQ}=90^0\)

\(\Rightarrow HQMP\) là hình chữ nhật

b) \(\Delta MPH\) vuông tại P

\(\Rightarrow HM^2=PM^2+PH^2\left(Pytago\right)\)

\(\Rightarrow PM^2=HM^2-PH^2=10^2-6^2=64\)

\(\Rightarrow PM=8\left(cm\right)\)

Diện tích HQMP:

\(S_{HQMP}=PM.PH=8.6=48\left(cm^2\right)\)

Sửa đề:

Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:

a) Tứ giác MQFE là hình bình hành

b) Trung điểm của MF thuộc đường thẳng QE

GIẢI 

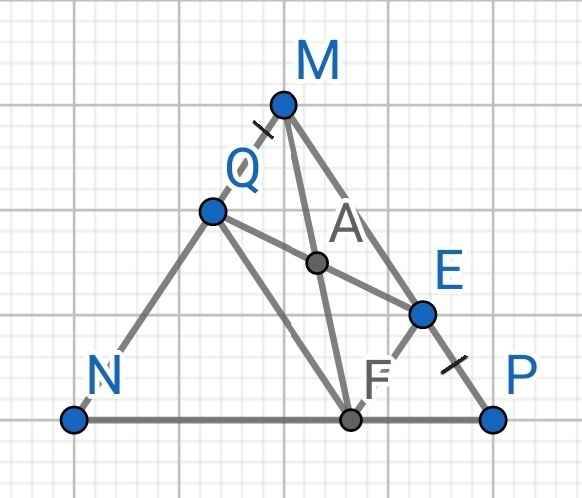
a) Do ∆MNP cân tại M (gt)

⇒ MN = MP

Mà MQ = PE (gt)

⇒ MN - MQ = MP - ME

⇒ QN = ME

Do QF // MP (gt)

⇒ ∠QFN = ∠MPN (đồng vị) (1)

Mà ∆MNP cân tại M

⇒ ∠MPN = ∠MNP

⇒ ∠MPN = ∠QNF (2)

Từ (1) và (2) ⇒ ∠QFN = ∠QNF

⇒ ∆QNF cân tại Q

⇒ QN = QF

Mà QN = ME (cmt)

⇒ QF = ME

Do QF // MP (gt)

⇒ QF // ME

Tứ giác MQFE có:

QF // ME (cmt)

QF = ME (cmt)

⇒ MQFE là hình bình hành

b) Gọi A là trung điểm của MF

Do MQFE là hình bình hành

⇒ A là trung điểm của hai đường chéo MF và QE

⇒ A là trung điểm của QE

⇒ A ∈ QE

Ta có

\(a+b+c=1\)

\(\Rightarrow\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)=1\)

Mà \(a^3+b^3+c^3=1\)

\(\Rightarrow3\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\)

\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=-b\\b=-c\\c=-a\end{matrix}\right.\)

Do a;b ;c bình đẳng nên giả sử a = - b

\(\Rightarrow a+b+c=1\)

\(\Leftrightarrow-b+b+c=1\Leftrightarrow c=1\)

\(A=a^n+b^n+c^n\) Do n là số TN lẻ nên

\(A=a^n+b^n+c^n=\left(-b\right)^n+b^n+c^n=-b^n+b^n+c^n=c^n=1^n=1\)

\(x^2+2xy+y^2-x-y\\=(x^2+2xy+y^2)-(x+y)\\=(x+y)^2-(x+y)\\=(x+y)(x+y-1)\\\text{#}Toru\)

    \(x^2\) + 2\(xy\) + y² - \(x\) - y

= (\(x\) + y)² - (\(x\) + y)

= (\(x\) + y).(\(x\) + y - 1)

`#3107.101107`

\((3x+7)(2x+3)-(3x-5)(2x+11)+3\)

`= 6x^2 + 9x + 14x + 21 - (6x^2 + 33x - 10x - 55) + 3`

`= 6x^2 + 23x + 21 - 6x^2 - 23x + 55 + 3`

`= (6x^2 - 6x^2) + (23x - 23x) + (21 + 55 + 3)`

`= 79`

Vậy, giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

(3x + 7)(2x + 3) - (3x - 5)(2x + 11) + 3

= 6x² + 9x + 14x + 21 - 6x² - 33x + 10x + 55 + 3

= (6x² - 6x²) + (9x + 14x - 33x + 10x) + (21 + 55 + 3)

= 89

Vậy giá trị của biểu thức đã cho không phụ thuộc vào giá trị của biến

Yêu cầu đề là gì bạn nên ghi chú rõ ra nhé.

\(x^2+2x-y^2+2y\\=(x^2-y^2)+(2x+2y)\\=(x-y)(x+y)+2(x+y)\\=(x+y)(x-y+2)\)

Đổi: 65 cm = 6,5 dm.

Thể tích hình hộp chữ nhật đó là:

$5\cdot5\cdot6,5=162,5(m^3)$

Vậy: ...

5 dm = 50 cm 

=> Thể tích của hình hộp chữ nhật là 

5 . 5 . 65 = 1625 ( cm³) 

               Đáp số : 1625 cm³