Gieo một con xúc xắc 6 mặt cân đối. Cho các biến bố sau:
A: “xuất hiện mặt có 5 chấm”.
B: “Xuất hiện mặt có số chấm nhỏ hơn 7”.
a) Hãy kiệt kê các kết quả có thể xảy ra khi gieo con xúc xắc trên.
b) Tính xác suất của biến cố A; B.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5:
a: Xét ΔABC có AB<AC
mà BH,CH lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
Xét ΔMBC có
HB<HC
mà HB,HC lần lượt là hình chiếu của MB,MC trên BC
nên MB<MC
b: Xét ΔBMH có \(\widehat{DMH}\) là góc ngoài tại M
nên \(\widehat{DMH}=\widehat{MHB}+\widehat{MBH}=90^0+\widehat{MBH}>90^0\)
Xét ΔDMH có \(\widehat{DMH}>90^0\)
nên DH là cạnh lớn nhất của ΔDMH
=>DH>DM

a; Biểu thức biểu thị số tiền mua y vở và mua x bút là:
6000 x \(x\) + 8000 x y
b; Số tiền dự định mua 5 cái bút và 15 quyển vở là:
6000 x 5 + 8000 x 15 = 150 000 (đồng)
Kết luận:..

a: Tổng số tiền phải trả khi mua x cái bút là 6000x(đồng)
Tổng số tiền phải trả khi mua y quyển vở là 8000y(đồng)
=>Q=6000x+8000y
b: Số tiền bạn Bình phải trả là:
\(Q=6000\cdot5+8000\cdot15=120000+30000=150000\left(đồng\right)\)
a, \(Q=x.6000+y.8000\)
b, Thay \(x=5\) và \(y=15\) vào đa thức \(Q\) , ta được:
\(Q=5.6000+15.8000\\ \Rightarrow Q=30000+120000\\ \Rightarrow Q=150000\left(nghìn\right)\)

a: Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)
Do đó: ΔACE=ΔAKE
=>AC=AK và EC=EK
AC=AK
nên A nằm trên đường trung trực của CK(1)
EC=EK
=>E nằm trên đường trung trực của CK(2)
Từ (1),(2) suy ra AE là đường trung trực củaCK
=>AE\(\perp\)CK
b: Xét ΔABC vuông tại C có \(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}+60^0=90^0\)
=>\(\widehat{CBA}=30^0\)
AE là phân giác của góc CAB
=>\(\widehat{CAE}=\widehat{BAE}=\dfrac{\widehat{CAB}}{2}=30^0\)
Xét ΔEAB có \(\widehat{EAB}=\widehat{EBA}\left(=30^0\right)\)
nên ΔEAB cân tại E
ΔEAB cân tại E
mà EK là đường cao
nên K là trung điểm của AB
=>KA=KB
c: Ta có: EB=EA
mà EA>AC(ΔEAC vuông tại C)
nên EB>AC
d: Xét ΔMAB có
AD,BC là các đường cao
AD cắt BC tạiE
Do đó: E là trực tâm của ΔMAB
=>ME\(\perp\)AB
mà EK\(\perp\)AB
và ME,EK có điểm chung là E
nên M,E,K thẳng hàng
=>AC,BD,KE đồng quy

a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot15=10\left(cm\right)\)
b: Xét ΔABM và ΔCEM có
MA=MC
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MB=ME
Do đó: ΔMAB=ΔMCE
=>\(\widehat{MAB}=\widehat{MCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BA//CE
d: Xét ΔNBF và ΔNAC có
\(\widehat{NBF}=\widehat{NAC}\)(BF//AC)
NB=NA
\(\widehat{BNF}=\widehat{ANC}\)(hai góc đối đỉnh)
Do đó: ΔNBF=ΔNAC
=>NF=NC
Xét ΔNAF và ΔNBC có
NA=NB
\(\widehat{ANF}=\widehat{BNC}\)(hai góc đối đỉnh)
NF=NC
Do đó: ΔNAF=ΔNBC
=>AF=BC
ΔNAF=ΔNBC
=>\(\widehat{NAF}=\widehat{NBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
Xét ΔMAE và ΔMCB có
MA=MC
\(\widehat{AME}=\widehat{CMB}\)(hai góc đối đỉnh)
ME=MB
Do đó: ΔMAE=ΔMCB
=>AE=CB
ΔMAE=ΔMCB
=>\(\widehat{MAE}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF(=BC)
nên A là trung điểm của EF

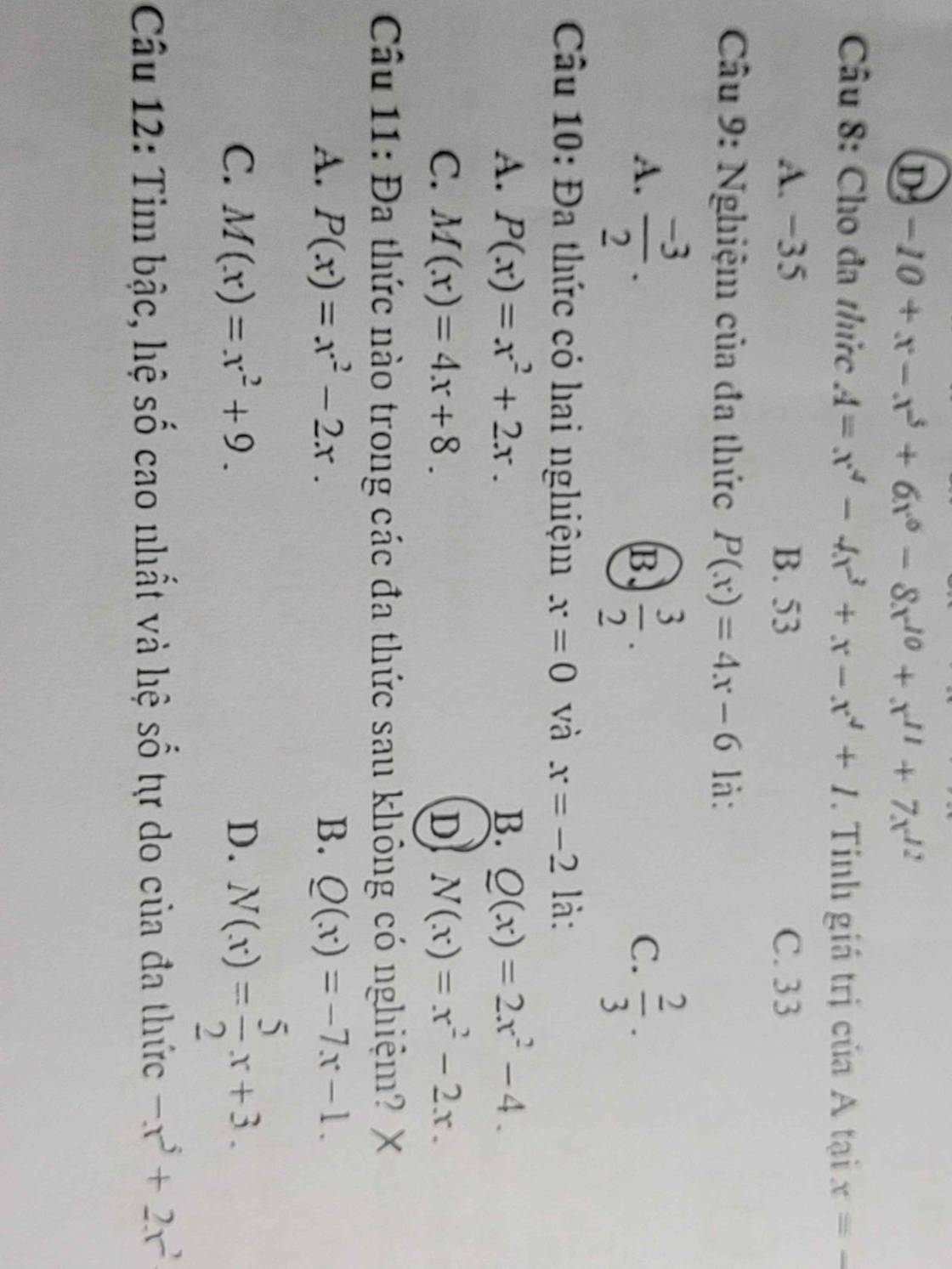

a) các kết quả có thể xảy ra: xuất hiện mặt 1 chấm, xhm 2c, xhm 3c, xhm 4c, xhm 5c, xhm 6c
b)Xác suất của biến cố A là \(\dfrac{1}{6}\)
Xác suất của biến cố B là 100%