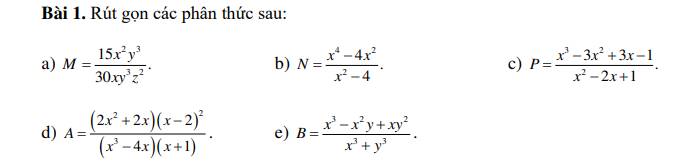
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



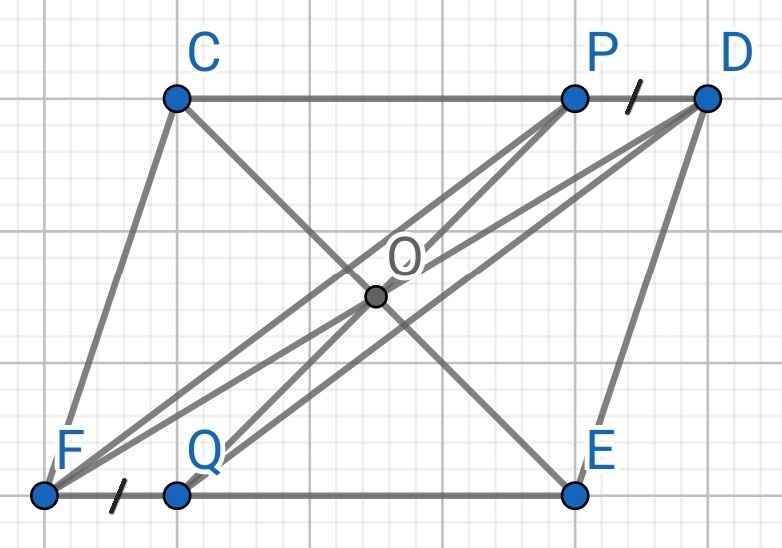 a) Sửa đề: Chứng minh PF // DQ
a) Sửa đề: Chứng minh PF // DQ
Do CDEF là hình bình hành (gt)
⇒ CD // EF
⇒ DP // FQ
Tứ giác DPFQ có:
DP // FQ (cmt)
DP = FQ (gt)
⇒ DPFQ là hình bình hành
⇒ PF // DQ
b) Do CDEF là hình bình hành (gt)
O là trung điểm của CE (gt)
⇒ O là trung điểm của DF
Mà DPFQ là hình bình hành
⇒ O là trung điểm của PQ

Vườn ông minh là hình vuông
Cạnh hình vuông là: 20 : 4 = 5 (m)
Chiều rộng hình chữ nhật sau khi tăng là: 5 + y (m)
Chiều dài hình chữ nhật sau khi tăng là: 8\(x\) (m)
Diện tích hình chữ nhật sau khi tăng là: 8\(x\).(5 + y) (m2)

Ta có:
\(M=x^2-2x\left(y+1\right)+3y^2+2025\)
\(M=x^2-2\cdot x\cdot\left(y+1\right)+\left(y+1\right)^2+3y^2+2025-\left(y+1\right)^2\)
\(M=\left[x-\left(y+1\right)\right]^2+3y^2+2025-y^2-2y-1\)
\(M=\left(x-y-1\right)^2+2y^2-2y+2024\)
\(M=\left(x-y-1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{4047}{2}\)
Mà: \(\left\{{}\begin{matrix}\left(x-y-1\right)^2\ge0\\2\left(y-\dfrac{1}{2}\right)^2\ge0\end{matrix}\right.\)
\(\Rightarrow M=\left(x-y-1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{4047}{2}\ge\dfrac{4047}{2}\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-y-1=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}+1\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy GTNN của M là ....


a) \(\left(2+x\right)^3=2^3+3.2^2.x+3.2.x^2+x^3\)
\(=8+12x+6x^2+x^3\)
b) \(\left(y+2\right)^3=y^3+3.y^2.2+3.y.2^2+2^3\)
\(=y^3+6y^2+12y+8\)
c) \(\left(2x+3\right)^3=\left(2x\right)^3+3.\left(2x\right)^2.3+3.2x.3^2+3^3\)
\(=8x^3+36x^2+54x+27\)

Lời giải:
$A=(9x^2+6xy+y^2)+y^2-6x+4y+17$
$=(3x+y)^2-2(3x+y)+y^2+6y+17$
$=(3x+y)^2-2(3x+y)+1+(y^2+6y+9)+7$
$=(3x+y-1)^2+(y+3)^2+7\geq 0+0+7=7$
Vậy GTNN của biểu thức là $7$. Giá trị này đạt được khi $3x+y-1=y+3=0$
$\Leftrightarrow y=-3; x=\frac{4}{3}$
$A$ không có max bạn nhé.

Ta có \(f\left(x\right)=\left(x+1\right)\left(x-3\right)\left(x+5\right)\left(x+9\right)+256\)
\(f\left(x\right)=\left(x+1\right)\left(x+5\right)\left(x-3\right)\left(x+9\right)+256\)
\(f\left(x\right)=\left(x^2+6x+5\right)\left(x^2+6x-27\right)+256\)
\(f\left(x\right)=\left[\left(x^2+6x-11\right)^2-256\right]+256\)
\(f\left(x\right)=\left(x^2+6x-11\right)^2\)

4.(\(x\) + 1)2 + (2\(x\) - 1)2 - 8.(\(x\) - 1)(\(x-1\) )= 11
4\(x^2\) + 8\(x\) + 4 + 4\(x^2\) - 4\(x\) + 1 - 8\(x^2\) + 16\(x\) - 8 = 11
(4\(x^2\) + 4\(x^2\) - 8\(x^2\)) + (8\(x\) - 4\(x\) + 16\(x\)) + (4 + 1 - 8) = 11
20\(x\) - 3 = 11
20\(x\) = 11 + 3
20\(x\) = 14
\(x\) = \(\dfrac{7}{10}\)
a) \(M=\dfrac{15x^2y^3}{30xy^3z^2}=\dfrac{15xy^3\cdot x}{15xy^3\cdot2z^2}=\dfrac{x}{2z^2}\left(x;y;z\ne0\right)\)
b) \(N=\dfrac{x^4-4x^2}{x^2-4}=\dfrac{x^2\left(x^2-4\right)}{x^2-4}=x^2\left(x\ne\pm2\right)\)
c) \(P=\dfrac{x^3-3x^2+3x-1}{x^2-2x+1}=\dfrac{x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3}{x^2-2\cdot x\cdot1+1^2}=\dfrac{\left(x-1\right)^3}{\left(x-1\right)^2}=x-1\left(x\ne1\right)\)
d) \(A=\dfrac{\left(2x^2+2x\right)\left(x-2\right)^2}{\left(x^3-4x\right)\left(x+1\right)}=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x^2-4\right)\left(x+1\right)}=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x+2\right)\left(x-2\right)\left(x+1\right)}=\dfrac{2\left(x-2\right)}{x+2}\left(x\ne0;x\ne\pm2;x\ne-1\right)\)e) \(B=\dfrac{x^3-x^2y+xy^2}{x^3+y^3}=\dfrac{x\left(x^2-xy+y^2\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{x}{x+y}\left(x\ne-y\right)\)