Tích của tử số và mẫu số của một phân số bằng 140, cả tử và mẫu của phân số đó đều là số chẵn. Vậy các phân số đó là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(x^2-2x-15=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot-15=64>0\)
Phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{2+\sqrt{64}}{2\cdot1}=5\)
\(x_2=\dfrac{2-\sqrt{64}}{2\cdot1}=-3\)
2) \(x^2-2mx+m-2=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(m-2\right)=4m^2-4m+8=\left(2m-1\right)^2+7>0\forall m\)
Theo vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2m\right)}{1}=2m\\x_1x_2=\dfrac{m-2}{1}=m-2\end{matrix}\right.\)
Ta có: \(\left(3+x_1\right)\left(2-x_2\right)-\left(3+x_2\right)\left(x_1-2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2-\left(-6+3x_1-2x_2+x_1x_2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2+6-3x_1+2x_2-x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-3\left(x_1+x_2\right)+2\left(x_1+x_2\right)-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-\left(x_1+x_2\right)=\left(x_1+x_2\right)^2+18\)
\(\Leftrightarrow12-2m=\left(2m\right)^2+18\)
\(\Leftrightarrow12-2m=4m^2+18\)
\(\Leftrightarrow4m^2+2m+6=0\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có m thỏa mãn

Nữa quãng đường từ nhà đến chợ là:
\(3880:2=1940\left(m\right)\)
Gấp 3 lần từ nhà đến công ty là:
\(1940+260=2200\left(m\right)\)
Quãng đường từ nhà đến công ty là:
\(2200:3=\dfrac{2200}{3}\left(m\right)\)
Đáp số: ...

\(\dfrac{x}{15}=\dfrac{-6}{5}\)
\(\Rightarrow x=\dfrac{-6}{5}\cdot15\)
\(\Rightarrow x=-6\cdot3\)
\(\Rightarrow x=-18\)
\(\dfrac{x}{15}=\dfrac{-6}{5}\\ \dfrac{x}{15}=\dfrac{-18}{15}\)
⇒\(x=-18\)
Vậy \(x=-18\)

a) \(\dfrac{-2}{5}< \dfrac{x}{15}< \dfrac{1}{6}\)
\(\Rightarrow\dfrac{-2\cdot6}{5\cdot6}< \dfrac{2\cdot x}{15\cdot2}< \dfrac{5\cdot1}{6\cdot5}\)
\(\Rightarrow-12< 2x< 5\)
\(\Rightarrow-6< x< \dfrac{5}{2}\)
Mà: x nguyên
\(\Rightarrow x\in\left\{-5;-4;-3;-2;-1;0;1;2\right\}\)
b) \(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{5}{12}< 2x< \dfrac{-12}{31}+\dfrac{-136}{-31}\)
\(\Rightarrow\dfrac{1}{6}-\dfrac{5}{12}< 2x< \dfrac{-12}{31}+\dfrac{136}{31}\)
\(\Rightarrow\dfrac{2}{12}-\dfrac{5}{12}< 2x< \dfrac{124}{31}\)
\(\Rightarrow-\dfrac{3}{12}< 2x< 4\)
\(\Rightarrow-\dfrac{1}{4}< x< 2\)
Mà x nguyên
\(\Rightarrow x\in\left\{0;1\right\}\)
a)\(\dfrac{-2}{5}< \dfrac{x}{15}< \dfrac{1}{6}\)
⇒\(\dfrac{-12}{30}< \dfrac{2.x}{30}< \dfrac{5}{30}\)
⇒\(-12< 2.x< 5\)
⇒\(2.x\)ϵ{\(-10;-8;-6;-4;-2;0;2;4\)}
⇒\(x\left\{-5;-4;-3;-2;-1;0;1;2\right\}\)

\(2-x=\dfrac{6}{5}\)
\(x=2-\dfrac{6}{5}\)
\(x=\dfrac{10}{5}-\dfrac{6}{5}\)
\(x=\dfrac{10-6}{5}\)
\(x=\dfrac{4}{5}\)
\(2-x=\dfrac{6}{5}\)
\(x=2-\dfrac{6}{5}\)
\(x=\dfrac{4}{5}\)
Vậy \(x=\dfrac{4}{5}\)

Phân số chỉ 35 mét đường còn lại là:
\(1-\dfrac{5}{9}-\dfrac{1}{4}=\dfrac{7}{36}\)
Đoạn đường cần sửa chữa dài:
\(35:\dfrac{7}{36}=180\left(m\right)\)
Đáp số: 180 m

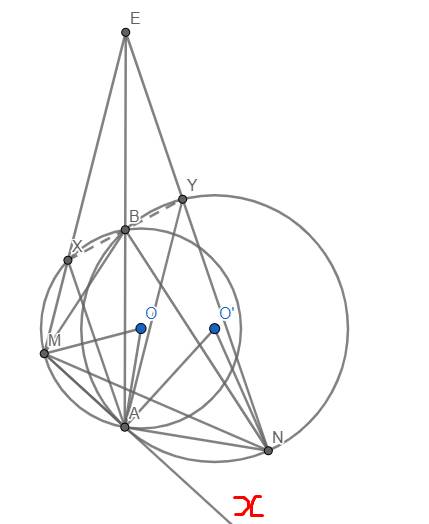
Gọi X và Y lần lượt là giao điểm thứ hai của EM với (O), EN với (O').
Ta có \(\widehat{MAO'}=\widehat{NAO}\left(=90^o\right)\) nên \(\widehat{MAO}=\widehat{NAO'}\). Hơn nữa tam giác MAO và NAO' đều là các tam giác cân nên \(\Rightarrow\widehat{MOA}=\widehat{NO'A}\)
Trong đường tròn (O), ta có: \(\widehat{MOA}=sđ\stackrel\frown{MA}=2.\dfrac{1}{2}sđ\stackrel\frown{MA}=2\widehat{MBA}\)
Tương tự, ta có \(\widehat{NO'A}=2\widehat{ABN}\)
\(\Rightarrow\widehat{MBA}=\widehat{ABN}\)
Hơn nữa có \(\widehat{MAB}=\widehat{ANB}\) (vì chúng lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AB của (O').
\(\Rightarrow\Delta BAM\sim\Delta BNA\left(g.g\right)\)
\(\Rightarrow\dfrac{BA}{BN}=\dfrac{BM}{BA}\)
Do \(BA=BE\) nên \(\dfrac{BE}{BN}=\dfrac{BM}{BE}\)
Lại có \(\widehat{MBA}=\widehat{ABN}\left(cmt\right)\) \(\Rightarrow\widehat{EBM}=\widehat{EBN}\)
\(\Rightarrow\Delta MBE\sim\Delta EBN\left(c.g.c\right)\)
\(\Rightarrow\widehat{MEB}=\widehat{ENB}\)
Lại có \(\widehat{ENB}=\widehat{BNY}=\widehat{BAY}\) nên \(\widehat{MEB}=\widehat{BAY}\) \(\Rightarrow\) EX//AY
\(\Rightarrow\widehat{AYN}=\widehat{MEN}\)
Hơn nữa vì \(\widehat{NAx}=\widehat{AYN}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung nhỏ AN trong (O'))
\(\Rightarrow\widehat{NAx}=\widehat{MEN}\)
Từ đó suy ra tứ giác AMEN nội tiếp (góc ngoài bằng góc trong đối)
Ta có đpcm.

Ta có:
\(\dfrac{2022}{2021}=\dfrac{2021+1}{2021}=1+\dfrac{1}{2021}\)
\(\dfrac{2021}{2020}=\dfrac{2020+1}{2020}=1+\dfrac{1}{2020}\)
Mà: \(2021>2020\)
\(\Rightarrow\dfrac{1}{2021}< \dfrac{1}{2020}\)
\(\Rightarrow1+\dfrac{1}{2021}< 1+\dfrac{1}{2020}\)
\(\Rightarrow\dfrac{2022}{2021}< \dfrac{2021}{2020}\)
\(\dfrac{2022}{2021}=1+\dfrac{1}{2021}\)
\(\dfrac{2021}{2020}=1+\dfrac{1}{2020}\)
Do \(2021>2020\Rightarrow\dfrac{1}{2021}< \dfrac{1}{2020}\)
\(\Rightarrow1+\dfrac{1}{2021}< 1+\dfrac{1}{2020}\)
Vậy \(\dfrac{2022}{2021}< \dfrac{2021}{2020}\)
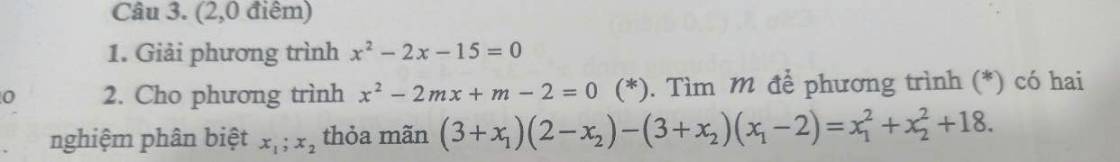
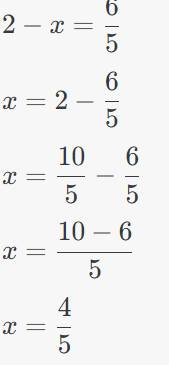
Do đó, các phân số thỏa mãn điều kiện là
35/35
34/36
33/37;
32/38
31/39