Tìm x,y,z biết:
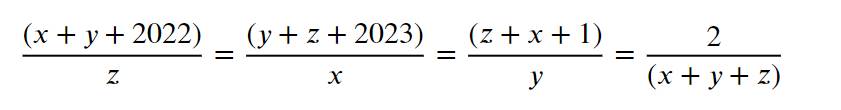
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(M\left(x\right)=x^2-3x+5x^4-mx-3\)
\(=5x^4+x^2+x\left(-m-3\right)-3\)
\(=5x^4+x^2+x\left(-m-3\right)-3\)
b: Hệ số cao nhất của M(x) là 2 nên \(5=2\)(vô lý)
=>\(m\in\varnothing\)

M(\(x\)) = \(x^2\) - 3\(x\) + 5\(x^4\) - 2\(x^2\) - m\(x\) - 3
M(\(x\)) = 5\(x^4\) + (\(x^2\) - 2\(x^2\)) - (3\(x\) + m\(x\)) - 3
M(\(x\)) = 5\(x^4\) - \(x^2\) - \(x\)(3 + m) - 3
Bậc của đa thức M(\(x\)) là 4
Hệ số cao nhất là 5

a: Xét ΔANB và ΔENM có
NA=NE
\(\widehat{ANB}=\widehat{ENM}\)(hai góc đối đỉnh)
NB=NM
Do đó: ΔANB=ΔENM
b: Ta có: \(AB=\dfrac{BC}{2}\)
\(BM=MC=\dfrac{BC}{2}\)
Do đó: AB=BM=MC
mà ME=AB(ΔNAB=ΔNEM)
nên MC=ME
=>ΔMEC cân tại M
c: N là trung điểm của MB
=>\(BN=NM=\dfrac{BM}{2}=\dfrac{CM}{2}\)
\(CM+MN=CN\)
=>\(CN=CM+\dfrac{1}{2}CM=\dfrac{3}{2}CM\)
=>\(CM=\dfrac{2}{3}CN\)
Xét ΔCAE có
CN là đường trung tuyến
\(CM=\dfrac{2}{3}CN\)
Do đó: M là trọng tâm của ΔCAE
d: Xét ΔAEC có
M là trọng tâm
EM cắt AC tại D
Do đó: D là trung điểm của AC

\(A\left(x\right)=0\Rightarrow x^2-4x+3=0\)
\(\Rightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow x-1=0\) hoặc \(x-3=0\)
\(\Rightarrow x=1\) hoặc \(x=3\)
Vậy đa thức đã cho có 2 nghiệm: \(x=1\); \(x=3\)
Đặt A(x)=0
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

\(x^3\left(x+2\right)-x\left(x^3+2^3\right)-2x\left(x^2-2^2\right)\)
\(=x^4+2x^3-x^4-8x-2x^3+8x\)
\(=0\)
x3(x + 2) - x(x3 + 23) - 2x(x2 - 22)
= x3.x + x3.2 + (-x).x3 + (-x).23 + (-2x).x2 + (-2x).(-22)
= x4 + 2x3 + (-x4) + (-x).8 + (-2x3) + (-2x).(-4)
= x4 + 2x3 - x4 + (-8x) - 2x3 + [(-2).(-4)]x
= x4 + 2x3 - x4 -8x - 2x3 + 8x
= (x4 - x4) + (2x3 - 2x3) + (-8x + 8x)
= 0.

a;
A(\(x\)) = \(x^3\) - 4\(x\) + a - 3; B(\(x\)) = \(x-2\)
Theo bezout ta có:
A(\(x\)) ⋮ B(\(x\)) ⇔ A(2) = 0
Thay \(x\) = 2 vào biểu thức A(\(x\)) = \(x^3\) - 4\(x\) + a - 3 = 0 ta có:
A(2) = 23 - 4.2 + a - 3 = 0
8 - 8 + a - 3 = 0
a - 3 = 0
a = 3
Vậy a = 3 thì A(\(x\)) ⋮ B(\(x\))